Stokes rotationssætning
|
|
|
- Ulrik Ibsen
- 9 år siden
- Visninger:
Transkript
1 enote 27 1 enote 27 Stokes rotationssætning I denne enote vil vi benytte Gauss divergenssætning fra enote 26 til at motivere, bevise, og illustrere Stokes sætning, som udtrykker en præcis sammenhæng mellem rotation og cirkulation af et givet vektorfelt: For enhver glat parametriseret flade F r er fluxen af rotationen af et glat vektorfelt V(x, y, z) igennem F r lig med cirkulationen af vektorfeltet langs randkurven F. Som hermed antydet får vi brug for både rum-, flade-, og kurve-integraler samt viden om vektorfelter og deres restriktioner til flader og kurver. Det vil sige, at basismaterialet for nærværende enote skal findes i en række enoter: enote 22 (om plan- og kurve-integraler), enote 23 (om fladeintegraler), enote 24 (om vektorfelter), enote 25 (om tangentielle kurveintegraler ogcirkulationer), og enote 26 (om flux-beregninger og Gauss sætning) Stokes sætning Figur 27.1: George Gabriel Stokes. Se Biografi.
2 enote STOKES SÆTNING 2 Stokes sætning er en af de mest elegante og mest benyttede resultater fra analysen af vektorfelter i rummet. Sætningen har ligesom Gauss divergenssætning mangfoldige anvendelser - f.eks. i fluid mekanik og i elektromagnetisme. Her er et citat som fortæller lidt om historien bag resultatet: The history of Stokes Theorem is clear but very complicated. It was first given by Stokes without proof - as was necessary since it was given as an examination question for the Smith s Prize Examination of that year [at Cambridge in 1854]! Among the candidates for the prize was Maxwell, who later traced to Stokes the origin of the theorem, which by 1870 was frequently used. On this see George Gabriel Stokes, Mathematical and Physical Papers, vol. V (Cambridge, England, 1905), See also the important historical footnote which indicates that Kelvin in a letter of 1850 was the first who actually stated the theorem, although others as Ampére had employed the same kind of analysis... in particular cases. M. J. Crowe, [A history of vector analysis, 1967], s Figur 27.2: James Clerk Maxwell (Biografi), William Thomson (Lord Kelvin) (Biografi), og Andrè-Marie Ampére (Biografi). Som antydet er Stokes resultat af samme kaliber som Gauss divergens-sætning. De er begge to medlemmer af en familie af resultater, hvor hovedideen er at omskrive et integral over et område til en andet integral over områdets rand - altså så at sige skubbe integrationen ud på randen. Det ældste medlem af den familie er Integralregningens fundamental-sætning, jvf. sætning enote 21 som vi gentager her med følgende formulering:
3 enote STOKES SÆTNING 3 Sætning 27.1 Integralregningens fundamentalsætning Lad f (u) betegne en kontinuert funktion på R. Så er følgende funktion differentiabel A(x) x 0 f (u) du med A (x) f (x). (27-1) Hvis F(x) er en (anden) funktion, som opfylder F (x) f (x), så er b a f (u) du F(b) F(a). (27-2) Her er nu formuleringen af Stokes sætning: Sætning 27.2 Stokes sætning Lad F r betegne en glat parametriseret flade med randkurven F r og enheds-normalvektorfelt n F og lad V være et glat vektorfelt i R 3. Så gælder F Rot(V) n F dµ F V e F dµ. (27-3) Ved beregning af højresiden skal orienteringen (givet ved retningen af enhedstangent-vektorfeltet e F ) af randen vælges således at krydsproduktet e F n F peger væk fra fladen langs med randen. Stokes sætning udtrykker altså ligesom (27-2) at et indre integral (her på et fladestykke) kan udtrykkes som et rand-integral (langs fladestykkets rand). Stokes sætning kan også formuleres som følger, idet vi henviser til definitionerne af flux og cirkulation i henholdsvis enote 26 og enote 25: Flux(Rot(V), F r ) Cirk(V, F). (27-4) Det vil sige: Fluxen af rotationen af vektorfeltet V igennem fladen F r er lig med cirkulationen af vektorfeltet langs fladestykkets lukkede randkurve F.
4 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 4 Læg mærke til, at hvis F r er hele overfladen af et rumligt område, så er F, og derfor følger det af Stokes sætning at Flux(Rot(V), F r ) 0 (27-5) i overensstemmelse med den følgesætning fra Gauss divergenssætning som er nævnt i sætning?? i enote Motivering af og et bevis for Stokes sætning Vi får brug for følgende resultat, som også er nævnt i afsnit 24.5 i enote 24: Sætning 27.3 Lad V(x, y, z) og W(x, y, z) betegne to vektorfelter i R 3. Så gælder følgende identitet Div(V W) Rot(V) W V Rot(W). (27-6) Specielt har vi derfor: Hvis W er et gradient-vektorfelt for en funktion ψ(x, y, z) i R 3, dvs. W (ψ), så får vi fra Rot( (ψ)) 0 : Div(V (ψ)) Rot(V) (ψ). (27-7) Ved at bruge Gauss divergens-sætning (sætning enote 26) i forbindelse med (27-7) får vi direkte et interessant resultat om integraler over rumlige områder således:
5 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 5 Sætning 27.4 En konsekvens af Gauss divergenssætning Lad ψ(x, y, z) betegne en glat funktion og V(x, y, z) et glat vektorfelt i R 3. Lad Ω være et rumligt område med randen Ω og udadrettet enheds-normalvektorfelt n Ω på Ω. Så har vi direkte fra Gauss sætning 26.15: Div(V (ψ)) dµ Ω Ω (V (ψ)) n Ω dµ. (27-8) Ved brug af (27-7) har vi derfor også Rot(V) (ψ) dµ Ω Ω (n Ω V) (ψ) dµ. (27-9) På højresiden i ligning (27-9) har vi benyttet, at rumproduktet [abc ] (a b) c af tre vektorer a, b, og c tilfredsstiller følgende identiteter (hvoraf vi har brugt den første): [abc ] [cab ] [bca ] [bac ] [cba ] [acb ]. (27-10) Specielt får vi den totale rotationsvektor af vektorfeltet V i Ω således: Følgesætning 27.5 Totale rotation i et rumligt område Lad Ω være et rumligt område med randen Ω og udadrettet enhedsnormalvektorfelt n Ω på Ω. Så gælder for ethvert glat vektorfelt V(x, y, z): Ω Rot(V) dµ Ω n Ω V dµ. (27-11) Bevis Dette følger direkte af (27-9) ved at vælge, skiftevis, ψ(x, y, z) x, ψ(x, y, z) y, og ψ(x, y, z) z, således at (ψ) er henholdsvis (1, 0, 0), (0, 1, 0), og (0, 0, 1). Højresiden af ligningen (27-11) vil vi tillade os at kalde den totale vridning af fladen Ω
6 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 6 med vektorfeltet V med hensyn til normalvektorfeltet n Ω og iøvrigt betegne denne vektor med Vrid(V, Ω) således: Definition 27.6 Vridning Lad F r betegne en glat flade i rummet med standard enheds-normalvetorfelt n F, og lad V(x, y, z) være et glat vektorfelt. Så definerer vi vridningen af F r med vektorfeltet V(x, y, z) på følgende måde: Vrid(V, F r ) F r n F V dµ. (27-12) Generelt er den totale rotation af et givet vektorfelt i et rumligt område (også kaldet total vorticity i fluid mekanik) altså via 27.5 lig med vridningen af områdets overflade med vektorfeltet. Dette minder meget om Gauss tilsvarende identitet for den totale divergens af et glat vektorfelt, sætning 26.15: Den totale divergens af vektorfeltet i et område er lig med fluxen af vektorfeltet ud igennem overfladen af området. I lighed med sætning har vi da også følgende tolkning og konstruktion af rotationsvektoren i et givet punkt: Sætning 27.7 Rotationen af et vektorfelt udtrykker den volumen-relative lokale vridning af overfladen for vektorfeltet i følgende forstand: Lad K ρ betegne en massiv kugle med radius ρ og centrum i punktet (x 0, y 0, z 0 ). Så gælder: ( ) 1 lim ρ 0 Vol(K ρ ) Vrid(V, K ρ) Rot(V)(x 0, y 0, z 0 ). (27-13)
7 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 7 Sætning 27.7 indses på samme måde som for den analoge identitet for divergensen. Vektorfeltet udvikles til første orden med udviklingspunkt p og indsættes i vridningsudtrykket, hvorefter følgende identiteter benyttes: x dµ y dµ z dµ 0, K ρ K ρ K ρ x 2 dµ y 2 dµ z 2 dµ (4 π/3) ρ 4 ρ Vol(K ρ ), K ρ K ρ K ρ x y dµ x z dµ z y dµ 0. K ρ K ρ K ρ (27-14) De eneste partielle afledede af vektorfeltets koordinatfunktioner, der ikke integreres væk, er præcis dem, der optræder i rotationsvektoren Rot(V) når denne evalueres i p. Prøv det! Eksempel 27.8 Lokal vridning af kugleflade giver rotationsvektoren Vi ser på et roterende vektorfelt V(x, y, z) ( y, x, 1). Dette felt har den konstante rotation Rot(V) (0, 0, 2). Vi vil vise, hvordan Vrid(V, K ρ ) netop giver denne rotation i punktet (0, 0, 0). Lad altså K ρ betegne den kugleflade, der har radius ρ, centrum i (0, 0, 0), og overflade K ρ med udadrettet normalvektorfelt n 1 ρ (x, y, z). Så er Vrid(V, K ρ ) n K V dµ K ρ 1 (x, y, z) ( y, x, 1) dµ ρ K ρ 1 ( y x z, x y z, x 2 + y 2 ) dµ ρ K ρ i overensstemmelse med sætning (0, 0, 2 Vol(K ρ ) ) Vol(K ρ ) Rot(V)(0, 0, 0), I mere komplicerede tilfælde kan den totale vridning af en flade med et givet vektorfelt beregnes med Maple. Hvis den aktuelle flade er randoverfladen af et givet rumligt område kan vridningen også beregnes som integralet af det tilhørende rotationsvektorfelt over det rumlige område. Derved muliggøres naturligvis også konkrete eftervisninger af ligning (27-11).
8 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING Fladen, randen, og normal-vektorfeltet De flader, der betragtes i Stokes sætning er parametriserede på sædvanlig vis: hvor F r : r(u, v) (x(u, v), y(u, v), z(u, v)) R 3, (27-15) (u, v) D [a, b] [c, d] R 2. (27-16) Randen F r af F r fremkommer ved at bruge vektorfunktionen r på de 4 rette linjestykker, der udgør randen D af det rektangulære parameterområde D [a, b] [c, d]. Vi parametriserer hele D på én gang ved hjælp af en parameter θ og en vektor-funktion d: D : d(θ) (u(θ), v(θ)) D R 2, θ I R, hvor u(θ) og v(θ) kun er stykkevis differentiable funktioner af θ. De kan f.eks. vælges som lineære funktioner af θ for hvert enkelt af de 4 linjestykker der udgør D. Randen af F r er så F r : b(θ) r(d(θ)) r(u(θ), v(θ)) R 3, θ I R. Jacobi-funktionerne for r og b er henholdsvis: Jacobi r (u, v) r u r v, og (27-17) Regulariteten af r giver Jacobi b (θ) b θ. (27-18) Jacobi r (u, v) > 0 for all (u, v) D. Enheds-normalvektorfeltet langs F r er tilsvarende n F n(u, v): n(u, v) r u r v r u r v for alle (u, v) D. (27-19) Tubulære skaller og en afstandsfunktion Vi definerer den tubulære skal med tykkelse t ud fra F r som følgende område i R 3 : Ω t : R(u, v, w) r(u, v) + w n(u, v), (u, v) D, w [0, t]. (27-20) Specielt er fladen F r netop basis-fladen for skallen og fås ved at bruge afbildningen R på D (hvor w 0): F 0 F R (0) F r : r(u, v) R(u, v, 0), (u, v) D. (27-21)
9 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 9 Figur 27.3: En tubulær skal der er defineret ved flow langs enheds-normalvektorfeltet n F fra et kvadrat. Tilsvarende får vi, for w t, top-fladen af skallen. Den er parametriseret således: Jacobi-funktionen for R er F t F R (t) F r : r(u, v) R(u, v, t), (u, v) D. (27-22) Jacobi R (u, v, w) ( R u R v) R w ( (r u + w n u) (r v + w n v) ) n F. (27-23) Da n F er et enhedsvektorfelt som er parallelt med r u r v langs F r, får vi specielt (for w 0): Jacobi R (u, v, 0) ( r u r v) nf r u r v Jacobi r (u, v) > 0. (27-24) Afbildningen R er regulær og bijektiv på D [0, t] - hvis blot t er tilstrækkelig lille. Det følger dels af Jacobi R (u, v, 0) > 0 og dels af kontinuiteten af Jacobi R (u, v, w). Værdien af w betragtet som en funktion på Ω t R 3 er en differentiabel funktion af de tre rum-variable (x, y, z). Selv om dette kan forekomme at være helt tydeligt, rent intuitivt, så er det faktisk et resultat, der finder sin bedste formulering og begrundelse i den såkaldte invers funktions-sætning, som dyrkes i kurset Matematik 3:
10 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 10 Figur 27.4: En tubulær skal der er defineret ved flow langs enheds-normalvektorfeltet n F fra et fladestykke af en kugleflade. Sætning 27.9 Invers funktionssætning Lad Q betegne en åben mængde i R 3 og lad f : Q R 3 betegne en differentiabel bijektiv afbildning med Jacobi f (x) > 0 for alle x Q. Så er den omvendte afbildning f 1 : f(q) Q også differentiabel med Jacobi f 1(y) > 0 for alle y f(q). Intuitionen er altså i dette tilfælde præcis og korrekt. Når t er tilstrækkelig lille, så er w en differentiabel funktion af de tre rum-variable, (x, y, z); lad os kalde den funktion h(x, y, z), (x, y, z) Ω t. Den funktion har så en egentlig gradient (h)(x, y, z), som er vinkelret på niveaufladerne for h. Specielt er (h) vinkelret på top-fladen F t F R (t) af skallen Ω t, hvor h t og den er tilsvarende vinkelret på basis-fladen F 0 F R (0) F r, hvor h 0. Gradienten (h) er faktisk præcis lig med n F på basis-fladen. For at indse dette behøver vi kun at vise, at længden af gradienten der er 1. Retningen er jo den samme. Lad derfor (u 0, v 0 ) betegne et punkt i D og betragt restriktionen af h til den rette linje r(u 0, v 0 ) + w n(u 0, v 0 ), hvor w [0, t]. Lad os benytte notationen r 0 r(u 0, v 0 ) og n 0 n(u 0, v 0 ).
11 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 11 Så giver kædereglen d 1 dw h(r 0 + w n 0 ) n 0 (h)(r 0 + w n 0 ) (h)(r 0 + w n 0 ), (27-25) således at vi på fladen F r, hvor w 0, har (h)(r 0 ) 1. Det var det, vi skulle vise. Vi har derfor: (h) F n F. (27-26) Funktionen h(x, y, z) er den Euklidiske afstand fra punktet (x, y, z) til fladen F r. Lokalt, dvs. tilstrækkeligt tæt på (og i normalretningen af) fladen F r er h(x, y, z) en udvidelse af enhedsnormalvektorfeltet n F til fladen. Vektorfeltet h(x, y, z) er selv et enhedsvektorfelt. Ved at lade F r flyde tiden t langs flowkurverne for h(x, y, z) dannes (udfejes) det rumlige område, den massive skal, Ω t, se figurerne 27.3, Integration i skallen For en funktion f (x, y, z) som er defineret i Ω t fås integralet af f over området således: f dµ Ω t ( t 0 D ) f (R(u, v, w)) Jacobi R (u, v, w) du dv dw. (27-27) Den t-afledede af dette integral er, for t 0, simpelthen fladeintegralet af f over F r : Hjælpesætning Fladeintegral som t-afledet af rumintegral ( ) d f dµ dt t0 Ω t F r f dµ. (27-28)
12 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 12 Bevis Det følger direkte af fundamentalsætningen 27.1: ( ) d f dµ dt t0 Ω t ( ) d t ( ) f (R(u, v, w)) Jacobi dt R (u, v, w) du dv dw t0 0 D f (R(u, v, 0)) Jacobi R (u, v, 0) du dv D f (r(u, v)) Jacobi r (u, v) du dv D f dµ. F r (27-29) The Wall - Væggen Skallen Ω t har en rand Ω t som består af top-fladen F t, basis-fladen F 0 F r F R (0) og en væg W t med højden t. Se figurerne 27.3 og Væg-komponenten fås ved restriktion af afbildningen R til D [0, t] således: W t : B(θ, w) R(u(θ), v(θ), w) r(u(θ), v(θ)) + w n(u(θ), v(θ)) b(θ) + w n(d(θ)), θ I, w [0, t]. (27-30) Jacobi-funktionen for denne afbildning er derfor Jacobi B (θ, w) B θ B w (b θ + w (n d) θ ) n F. (27-31) Da n F står vinkelret på fladen F r og derfor også på randen F r (parametriseret via b), får vi: Jacobi B (θ, 0) b θ n F b θ Jacobi b(θ). (27-32) Integration langs væggen t For en given funktion g(x, y, z) defineret på W t fås integralet af g over den flade: t ( ) g dµ W g(b(θ, w)) Jacobi B (θ, w) dθ dw. (27-33) 0 I
13 enote MOTIVERING AF OG ET BEVIS FOR STOKES SÆTNING 13 Den t-afledede af dette integral er, for t 0, kurve-integralet af g over F: Hjælpesætning Kurveintegral som t-afledet af fladeintegral ( ) d g dµ dt t0 W t F g dµ. (27-34) Bevis Det følger igen af fundamentalsætningen, Sætning 27.1: ( ) d g dµ dt t0 W t ( ) d t ( ) g(b(θ, w)) Jacobi dt B (θ, w) dθ dw t0 0 I g(b(θ, 0)) Jacobi B (θ, 0) dθ I g(b(θ)) Jacobi b (θ) dθ I g dµ. F (27-35) Bevis for Stokes sætning Vi er nu parate til at bevise Sætning Bevis Funktionen h(x, y, z) fra det foregående afsnit indsættes i stedet for ψ(x, y, z) i Sætning 27.4, ligning (27-9). Med integrations-området Ω Ω t får vi så: Rot(V) (h) dµ Ω t (n Ωt V) (h) dµ Ω t (n Ft V) (h) dµ (27-36) F t (n F0 V) (h) dµ F 0 + (n Wt V) (h) dµ. W t
14 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 14 Men i ligning (27-36) har vi F t (n Ft V) (h) dµ 0 og F 0 (n F0 V) (h) dµ 0, (27-37) idet (h) er vinkelret på begge fladerne F t og F 0 således at (h) er proportional med henholdsvis n Ft og n F0 på de respektive flader. Langs F W t har vi n Wt e F n F og derfor e F n F n Wt - i overensstemmelse med orienterings-reglen i Sætning Hvis vi t-afleder begge sider af den reducerede ligning (27-36) får vi: ( ) d dt ( ) d dt t0 t0 Rot(V) (h) dµ Ω t W t (n Wt V) (h) dµ, således at vi endelig har - i kraft af ligningerne (27-28) og (27-34): Stokes sætning er dermed bevist. F F F F Rot(V) n F dµ (n Wt V) n F dµ V (n F n Wt ) dµ V e F dµ. (27-38) (27-39) 27.3 Verificering af Stokes sætning i konkrete eksempler I lighed med Gauss divergens-sætning kan Stokes sætning verificeres ved i konkrete givne tilfælde at beregne begge sider af identiteten (27-3) i Stokes sætning. Eksempel Stokes sætning med en cirkelskive En standard cirkelskive i (x, y)-planen er givet ved sin sædvanlige parameterfremstilling: F r : r(u, v) (u cos(v), u sin(v), 0), (u, v) [0, 1] [ π, π] (27-40) med Jacobifunktionen Jacobi r (u, v) u, (27-41)
15 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 15 standard enhedsnormalvektorfelt til fladen n F (0, 0, 1), (27-42) og standard enheds-tangentvektorfelt langs den cirkulære rand F: e F r v(1, v) ( sin(v), cos(v), 0). (27-43) Bemærk, at det er r(1, v), v [ π, π], der giver hele randen, at r v(1, v) er en enhedsvektor for alle v, og at r v(1, v) n F peger væk fra cirkelskiven langs hele randkurven. Et glat vektorfelt i rummet er givet ved sine koordinatfunktioner således: og har det tilhørende rotationsvektorfelt V(x, y, z) (x y, x, x 2 ), (27-44) Rot(V)(x, y, z) (0, 2 x, 1 x). (27-45) Vi vil verificere Stokes sætning ved at beregne begge sider af ligning (27-3) i dette konkrete tilfælde. Den totale flux af vektorfeltet Rot(V)(x, y, z) igennem F r i retning af standardenhedsnormalen n F (0, 0, 1) er Flux(Rot(V), F r ) Rot(V) n F dµ F r (1 x) dµ F r π π π π π. 1 (1 u cos(v)) u du dv 0 ( ) 3 cos(v) dv (27-46) Cirkulationen af vektorfeltet V(x, y, z) langs F r i retning af standard-enhedstangentvektorfeltet e F ( sin(v), cos(v), 0) er Cirk(V, F) V e F dµ 1 2 F π π π π π π π π π π π 1 2 π. V(r(1, v)) ( sin(v), cos(v), 0) dv (cos(v) sin(v), cos(v), ) ( sin(v), cos(v), 0) dv ( cos(v) sin 2 (v) + cos 2 (v)) dv cos 2 (v) dv π ( cos 2 (v) + sin 2 (v) ) dv 1 dv (27-47)
16 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 16 Begge sider i ligningen (27-3) giver altså π i dette eksempel og vi har derfor verificeret Stokes sætning. Figur 27.5: En cirkelskive i et vektorfelt V(x, y, z) (x y, x, x 2 ) (i midten) og vektorfeltets rotationsvektorfelt Rot(V)(x, y, z) (0, 2 x, 1 x). Eksempel Stokes sætning med en paraboloide Et udsnit af en paraboloide er givet ved en parameterfremstilling således: F r : r(u, v) (2 u cos(v), 2 u sin(v), u 2 ), (27-48) hvor (u, v) [1/2, 1] [0, π] (27-49) Parameterfremstillingen har Jacobifunktionen Jacobi r (u, v) 4 u cot 1 + u 2, (27-50) og standard-normalvektorfeltet (ikke nødvendigvis enheds-vektorer) til fladen er givet ved N F (u, v) r u(u, v) r v(u, v) ( 4 u 2 cos(v), 4 u 2 sin(v), 4 u). (27-51) Et glat vektorfelt i rummet er givet ved sine koordinatfunktioner således: V(x, y, z) (z, y, x), (27-52)
17 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 17 Figur 27.6: Restriktionen af rotationsvektorfeltet Rot(V)(x, y, z) (0, 2 x, 1 x) til en cirkelskive, cirkelskivens rand, og vektorfeltet V(x, y, z) (x y, x, x 2 ) restringeret til randen. med det tilhørende rotationsvektorfelt Rot(V)(x, y, z) (0, 2, 0). (27-53) Vi vil verificere Stokes sætning ved at beregne begge sider af ligning (27-3) i dette konkrete tilfælde. Den totale flux af vektorfeltet Rot(V)(x, y, z) igennem F r i retning af standardenhedsnormalen er, idet vi benytter normalvektorfeltet N F (u, v) direkte: Flux(Rot(V), F r ) Rot(V) n F dµ F r π 1 0 1/2 π 1 0 π /2 Rot(V) N F (u, v) du dv ( 8 u2 sin(v) ) du dv ( 7 3 sin(v). ) dv (27-54) Cirkulationen af vektorfeltet V(x, y, z) langs F r i retning af den korrekt orienterede randkurve består af fire komponenter. De fås fra fladens parameterfremstilling r(u, v) dels ved at fastholde v til at være henholdsvis 0 og π, og dels ved at fastholde u til at være henholdsvis 1/2 og 1, idet det i hvert tilfælde samtidigt sikres, at den frie parameter løber den rigtige
18 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 18 vej, dvs. således at alle fire randkomponenter får den rette orientering i forhold til fladens normalvektorfelt: 1 F : r 1 (u) r(u, 0) (2 u, 0, u 2 ), u [1/2, 1] r 1(u) (2, 0, 2 u) V(r 1 (u)) (u 2, 0, 2 u) r 1(u) V(r 1 (u)) 2 u 2, (27-55) 3 F : r 3 (u) r(1 u + 1/2, v) ( u, 0, ( 3/2 + u) 2 ), u [1/2, 1] r 3(u) (2, 0, 2 u 3) V(r 3 (u)) (( 3/2 + u) 2, 0, 3 2 u) r 3(u) V(r 3 (u)) u 2 u2, (27-56) 2 F : r 2 (v) r(1, v) (2 cos(v), 2 sin(v), 1), v [0, π] r 2(v) ( 2 sin(v), 2 cos(v), 0) V(r 2 (v)) (1, 2 sin(v), 2 cos(v)) r 2(v) V(r 2 (v)) 2 sin(v) (2 cos(v) 1), 4 F : r 4 (v) r(1/2, π v) ( cos(v), sin(v), 1/4), v [0, π] r 4(v) (sin(v), cos(v), 0) V(r 4 (v)) ( 1, sin(v), cos(v)) 4 (27-57) (27-58) r 4(v) V(r 4 (v)) 1 sin(v) (cos(v) + 1). 4 Vi har dermed følgende totale cirkulation af V(x, y, z) langs randen: Cirk(V, F) 4 Cirk(V, i F) i1 4 i1 i F 1 1/ /2 π V(r i (t)) r i (t) dt ( 2 u 2 ) du ( ) u 2 u2 du sin(v) (2 cos(v) 1) dv π 1 + sin(v) (cos(v) + 1) dv (27-59)
19 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 19 Begge sider i ligningen (27-3) giver altsa 14/3 i dette eksempel, og vi har sa ledes igen verificeret Stokes sætning. Figur 27.7: Et stykke af en paraboloide i et vektorfelt V( x, y, z) (z, y, x ) (i midten) og vektorfeltets rotationsvektorfelt Rot(V)( x, y, z) (0, 2, 0). Opgave Lad Fr betegne den flade, der har følgende parameterfremstilling og parameter-omra de: Fr : r(u, v) ((1 + u2 ) cos(v), (1 + u2 ) sin(v), sin(u)), (27-60) hvor π π π (u, v) [, ] [ π, ]. (27-61) Verifice r at Stokes sætning er opfyldt for vektorfeltet V (yx, yz, xz) over fladen Fr med den givne rand Fr. Opgave Lad Fr betegne den flade et sa kaldt Mo bius-ba nd der har følgende parameterfremstilling og parameter-omra de: Fr : r(u, v) (2 cos(u) + v cos(u/2) cos(u), 2 sin(u) + v cos(u/2) sin(u), v sin(u/2)), (27-62)
20 enote VERIFICERING AF STOKES SÆTNING I KONKRETE EKSEMPLER 20 Figur 27.8: Restriktionen af rotationsvektorfeltet Rot(V)(x, y, z) (0, 2, 0) til et stykke af en paraboloide, fladestykkets rand, og vektorfeltet V(x, y, z) (z, y, x) restringeret til randen. hvor (u, v) [ π, π] [ 1, 1]. Verificér at Stokes sætning er opfyldt for vektorfeltet V ( y, x, 1) over fladen F r med den givne rand F r, se Figur 27.10: Vis eksplicit, at der gælder: F Rot(V) n F dµ F V e F dµ 32. (27-63) Opgave Lad nu G r betegne det samme Møbius-bånd som i opgave 27.15: G r : r(u, v) (2 cos(u) + v cos(u/2) cos(u), 2 sin(u) + v cos(u/2) sin(u), v sin(u/2)), (27-64) men nu med et lidt modificeret parameterområde: (u, v) [0, 2π] [ 1, 1]. (27-65) Verificér at Stokes sætning er opfyldt for vektorfeltet V ( y, x, 1) over fladen G r med den givne rand G r : Vis eksplicit, at der gælder: G r Rot(V) n G dµ G r V e G dµ 0. (27-66)
21 enote STOKES SÆTNING I PLANEN 21 Figur 27.9: August Ferdinand Möbius, se Biografi. Opgave Forklar forskellen mellem de to (værdi-)resultater (henholdsvis 32 og 0), der opnås i henholdsvis (27-63) og (27-66). Vink: Hold øje med normalvektorfeltet n F. Hvilke værdier for rotationsflux og cirkulation opnås ved at skifte intervaller i parametriseringen, dvs. ved blot at benytte følgende parameterintervaller for forskellige α R: (u, v) [ π + α, π + α] [ 1, 1]? (27-67) 27.4 Stokes sætning i planen Plane områder, for eksempel områder i (x, y) planen, kan parametriseres således: F r : r(u, v) (x(u, v), y(u, v), 0) R 3, (u, v) D [a, b] [c, d] R 2. (27-68) Et plant område har et særligt simpelt enhedsnormal-vektorfelt i rummet, dvs. når vi betragter det plane område som en flade i rummet, der tilfældigvis ligger helt i (x, y) planen: n F (0, 0, 1). Med hensyn til randen af det plane område repeterer vi notationen fra afsnit : Randen F r af F r fremkommer ved at bruge vektorfunktionen r på de 4 rette linjestykker, der udgør randen D af det rektangulære parameterområde D [a, b] [c, d]. Vi parametriserer hele D på én gang ved hjælp af en parameter θ og en vektor-funktion d: D : d(θ) (u(θ), v(θ)) D R 2, θ I R,
22 enote STOKES SÆTNING I PLANEN 22 Figur 27.10: Et Mo bius ba nd i et vektorfelt V( x, y, z) ( y, x, 1) (i midten) og vektorfeltets rotationsvektorfelt Rot(V)( x, y, z) (0, 0, 2). hvor u(θ ) og v(θ ) kun er stykkevis differentiable funktioner af θ. De kan f.eks. vælges som lineære funktioner af θ for hvert enkelt af de 4 linjestykker der udgør D. Randen af Fr er sa Fr : b(θ ) r(d(θ )) r(u(θ ), v(θ )) R2 R3, θ I [0, T ] R. (27-69) Lad nu V( x, y, z) (V1 ( x, y, z), V2 ( x, y, z), V3 ( x, y, z)) betegne et vilka rligt vektorfelt i rummet, sa har vi følgende konsekvens af Stokes sætning:
23 enote STOKES SÆTNING I PLANEN Figur 27.11: Restriktionen af rotationsvektorfeltet Rot(V)( x, y, z) (0, 0, 2) til et stykke af et Mo bius ba nd, ba ndets rand, og vektorfeltet V( x, y, z) ( y, x, 1) restringeret til randen. Sætning Stokes sætning i planen Med ovensta ende notation gælder: Z Fr Z Fr Z Rot(V) nf dµ Rot(V) (0, 0, 1) dµ Z V e F dµ F Z (V1, V2, V3 ) e F dµ F (27-70) Z (V1, V2, V3 ) b0 (θ ) dθ Rot(V) (0, 0, 1) dµ Fr I Z Z T V2 V1 dµ V1 b10 (θ ) + V2 b20 (θ ) dθ x y Fr 0, og dermed Z dz b Z T V2 V1 Jacobir (u, v) du dv V1 b10 (θ ) + V2 b20 (θ ) dθ x y 0 c a. (27-71)
24 enote STOKES SÆTNING I PLANEN 24 Bemærkning Det ses, at vektorfeltets tredie koordinat-funktion V 3 (x, y, z) ikke spiller nogen rolle i sætningen. Sætningen er derfor et resultat om vektorfunktioner i planen: V(x, y) (V 1 (x, y), V 2 (x, y)). Vi illustrerer med et detaljeret - men simpelt - eksempel nedenfor. Eksempel Stokes sætning i planen Lad V(x, y) ( y, x) og r(u, v) (3u, 4v), u [a, b], v [c, d], så får vi: Jacobi r (u, v) 12 og V 2 x V 1 y 2 sådan at venstre side i ligning (27-71) giver: d b ( V2 x V ) 1 Jacobi y r (u, v) du dv c a d b c a 2 12 du dv 24(b a)(d c). Højre side i ligning (27-71) skal give samme værdi. (27-72) Vi bestemmer højre sides værdi ved at opdele randen af F r i 4 retlinede komponenter og ved at beregne det tangentielle kurveintegral af V langs hver komponent, idet vi i hvert tilfælde sørger for at orientere (parametrisere) komponenten korrekt efter den forskrift, som er præciseret i Stokes sætning. Vi begynder med at sætte T 2(b a) + 2(d c), dvs. T er den totale omkreds af parameterområdet D. Randen af D kan vi så parametrisere på følgende måde: d(θ) (a + θ, 0) for θ [0, b a] d(θ) (b, c + θ) for θ [b a, b a + d c] d(θ) (b θ, d) for θ [b a + d c, 2(b a) + d c] d(θ) (a, d θ) for θ [2(b a) + d c, 2(b a) + 2(d c)]. Randen af F r har vi dernæst på følgende form: b(θ) (3(a + θ), 0) for θ [0, b a] b(θ) (3b, 4(c + θ)) for θ [b a, b a + d c] b(θ) (3(b θ), 4d) for θ [b a + d c, 2(b a) + d c] b(θ) (3a, 4(d θ)) for θ [2(b a) + d c, 2(b a) + 2(d c)], og dermed: b (θ) (3, 0) for θ [0, b a] b (θ) (0, 4) for θ [b a, b a + d c] b (θ) ( 3, 0) for θ [b a + d c, 2(b a) + d c] b (θ) (0, 4) for θ [2(b a) + d c, 2(b a) + 2(d c)]. (27-73) (27-74) (27-75)
25 enote STOKES SÆTNING I PLANEN 25 Vi kan nu beregne højresiden i ligning (27-71) som summen af de 4 led, der stammer fra hver sin komponent af randkurven. For eksempel, for det første linjestykke i randkurven, som er parallel med x aksen og med konstant y 4c har vi: θ [0, b a] har vi b 1 (θ) 3, b 2 (θ) 0, V 1 (x, y) y b 2 (u, v) 4v 4c og ligeledes for de andre 3 bidrag (se figurerne og 27.13): T V 1 b 1(θ) + V 2 b 2(θ) dθ b a 12c dθ 0 b a+d c b a 2(b a)+d c 12b dθ b a+d c 2(b a)+2(d c) 2(b a)+d c 12c(b a) + 12b(d c) + 12d(b a) + 12a(d c) 12d dθ 12a dθ 24(b a)(d c), (27-76) i overensstemmelse med resultatet i ligning (27-72), sådan at den generelle ligning (27-71) dermed er verificeret i dette tilfælde.
26 enote STOKES SÆTNING I PLANEN 26 Figur 27.12: 3D versionering af eksempel Vektorfeltet V( x, y) ( y, x, 0) har rotationsvektorfeltet (0, 0, 2). Her er valgt et kvadrat med parameterfremstilling r(u, v) (3u, 4v, 0), u [ a, b], v [c, d], a 1/3, b 1/3, c 1/4, og d 1/4. Figur 27.13: Opstilling af fluxen af rotationsvektorfeltet Rot(V( x, y, z) (0, 0, 2) igennem kvadrat i ( x, y)-planen og tilhørende cirkulation af vektorfeltet V( x, y, z) ( y, x, 0) langs den firkantede randkurve.
27 enote OPSUMMERING Opsummering Vi har set her, at fluxen af et rotationsvektorfelt Rot(V)(x, y, z) igennem en flade kan beregnes som cirkulationen af V(x, y, z) langs randkurven til fladen passende orienteret. Lad F r betegne en glat parametriseret flade med randkurven F r og enheds-normalvektorfelt n F og lad V være et glat vektorfelt i R 3. Så udtrykker Stokes sætning følgende identitet F Rot(V) n F dµ F V e F dµ. (27-77) Ved beregning af højresiden er det vigtigt (for at få det korrekte fortegn) at orienteringen af randen vælges sådan at krydsproduktet e F n F peger væk fra fladen langs med randen. Alternativt kan Stokes sætning udtrykkes således: Fluxen af rotationen af vektorfeltet V igennem fladen F r er lig med cirkulationen af vektorfeltet langs fladestykkets lukkede randkurve F: Flux(Rot(V), F r ) Cirk(V, F). (27-78) Den Totale rotation af et vektorfelt i et rumligt område kan tilsvarende beregnes ved fladeintegral over den totale overflade af området: Lad Ω være et rumligt område med randen Ω og udadrettet enheds-normalvektorfelt n Ω på Ω. Så gælder for ethvert glat vektorfelt V(x, y, z): Ω Rot(V) dµ Ω n Ω V dµ Vrid(V, Ω). (27-79)
Vektorfelter langs kurver
 enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
enote 25 1 enote 25 Vektorfelter langs kurver I enote 24 dyrkes de indledende overvejelser om vektorfelter. I denne enote vil vi se på vektorfelternes værdier langs kurver og benytte metoder fra enote
Kurve- og plan-integraler
 enote 22 1 enote 22 Kurve- og plan-integraler Vi vil her med udgangspunkt i de metoder og resultater der er opstillet i enote 21 vise, hvordan Riemann-integralerne derfra kan benyttes til blandt andet
enote 22 1 enote 22 Kurve- og plan-integraler Vi vil her med udgangspunkt i de metoder og resultater der er opstillet i enote 21 vise, hvordan Riemann-integralerne derfra kan benyttes til blandt andet
Vektorfelter. enote Vektorfelter
 enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
enote 24 1 enote 24 Vektorfelter I enote 6 indføres og studeres vektorer i plan og rum. I enote 16 ser vi på gradienterne for funktioner f (x, y) af to variable. Et gradientvektorfelt for en funktion af
Flade- og rum-integraler
 enote 25 1 enote 25 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
enote 25 1 enote 25 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
Gradienter og tangentplaner
 enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
enote 16 1 enote 16 Gradienter og tangentplaner I denne enote vil vi fokusere lidt nærmere på den geometriske analyse og inspektion af funktioner af to variable. Vi vil især studere sammenhængen mellem
Eksamen maj 2018, Matematik 1, DTU
 Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Eksamen maj 2018, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots!
Flade- og rum-integraler
 enote 23 1 enote 23 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
enote 23 1 enote 23 Flade- og rum-integraler Flade og rumintegraler opstilles her på stort set samme måde som kurve- og planintegralerne i enote 22, som derved sammen med den grundlæggende generelle indførelse
Funktioner af to variable
 enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
enote 15 1 enote 15 Funktioner af to variable I denne og i de efterfølgende enoter vil vi udvide funktionsbegrebet til at omfatte reelle funktioner af flere variable; vi starter udvidelsen med 2 variable,
Mat 1. 2-timersprøve den 13. maj 2017.
 Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
Mat. -timersprøve den. maj 7. JE.5.7 Opgave restart:with(plots): En funktion f af to reelle variable er for x, y s, givet ved f:=(x,y)-y/(x^+y^); f d x, y / y x Cy f(x,y); y x Cy Spørgsmål I x, y Kplanen
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
OPGAVE 1 Det nedenstående klip er fra et Maple-ark hvor en reel funktion f (x, y) med definitionsmængden (x,y) x 2 + y 2 < 1 } bliver undersøgt:
 DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
DANMARKS TEKNISKE UNIVERSITET Skriftlig prøve den 7. maj 00. Kursus Navn: Matematik (-timers prøve for forårssemesteret). Kursus nr. 0005 Tilladte hjælpemidler: Alle af DTU tilladte hjælpemidler må medbringes
Andengradsligninger i to og tre variable
 enote 0 enote 0 Andengradsligninger i to og tre variable I denne enote vil vi igen beskæftige os med andengradspolynomierne i to og tre variable som også er behandlet og undersøgt med forskellige teknikker
enote 0 enote 0 Andengradsligninger i to og tre variable I denne enote vil vi igen beskæftige os med andengradspolynomierne i to og tre variable som også er behandlet og undersøgt med forskellige teknikker
Maj 2015 (alle opgaver og alle spørgsmål)
 Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Maj 2015 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Ved eksamen er der ikke tid til f.eks. at lave illustrationer,
Gauss divergenssætning
 enote 26 1 enote 26 Gauss divergenssætning I denne enote vil vi bruge flowkurver for vektorfelter til at undersøge hvordan overfladen af et rumligt område deformeres ved flowet og dermed afspejler en tilsvarende
enote 26 1 enote 26 Gauss divergenssætning I denne enote vil vi bruge flowkurver for vektorfelter til at undersøge hvordan overfladen af et rumligt område deformeres ved flowet og dermed afspejler en tilsvarende
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 9. november 25 Divergens af et vektorfelt [Sektion 9.8 og.7 i bogen, s. 43]. Definition af og og egenskaber for divergens Lad
(c) Opskriv den reelle Fourierrække for funktionen y(t) fra (b), og afgør dernæst om y(t) er en lige eller ulige funktion eller ingen af delene.
 MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
MATEMATIK 3 EN,MP 4. februar 2016 Eksamenopgaver fra 2011 2016 (jan. 2016) Givet at 0 for 0 < t < 1 mens e (t 1) cos(7(t 1)) for t 1, betragt da begyndelsesværdiproblemet for t > 0: y (t) + 2y (t) + 50y(t)
Maj 2013 (alle opgaver og alle spørgsmål)
 Maj 2013 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Jeg gider ikke håndregne i de simple spørgsmål! Her
Maj 2013 (alle opgaver og alle spørgsmål) Alternativ besvarelse (med brug af Maple til beregninger, incl. pakker til VektorAnalyse2 og Integrator8). Jeg gider ikke håndregne i de simple spørgsmål! Her
Eksamen maj 2019, Matematik 1, DTU
 Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
Eksamen maj 2019, Matematik 1, DTU NB: Nedenstående udregninger viser flere steder mere end én metode. Det er der IKKE tid til eksamen! Ligeledes er der ikke krav om eller tid til at illustrere med plots.
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner R n R m Differentiable funktioner
Mat 1. 2-timersprøve den 17. maj 2016.
 Mat -timersprøve den 7 maj 6 JE 6 Opgave restart; Givet funktionen f:=x-sqrt(*x-); Spørgsmål f := x/ x K Funktionen er defineret for x K R x R Dvs Dm f er intervallet [ ;N[ Spørgsmål Med udviklingspunktet
Mat -timersprøve den 7 maj 6 JE 6 Opgave restart; Givet funktionen f:=x-sqrt(*x-); Spørgsmål f := x/ x K Funktionen er defineret for x K R x R Dvs Dm f er intervallet [ ;N[ Spørgsmål Med udviklingspunktet
Partielle afledede og retningsafledede
 Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Supplement til Matematik 1GB. Jan Philip Solovej
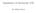 Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Supplement til Matematik 1GB Jan Philip Solovej ii c 2001 Jan Philip Solovej, Institut for Matematiske Fag, Københavns Universitet. Alle har tilladelse til at reproducere hele eller dele af dette materiale
Geometriske grundbegreber 8. lektion
 1 / 14 Geometriske grundbegreber 8. lektion Martin Raussen Institut for matematiske fag Aalborg Universitet 1.4.2008 2 / 14 (Regulære) parameterfremstillinger for en flade Eksempler Kurver på flader og
1 / 14 Geometriske grundbegreber 8. lektion Martin Raussen Institut for matematiske fag Aalborg Universitet 1.4.2008 2 / 14 (Regulære) parameterfremstillinger for en flade Eksempler Kurver på flader og
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Epistel E2 Partiel differentiation
 Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
Epistel E2 Partiel differentiation Benny Lautrup 19 februar 24 Funktioner af flere variable kan differentieres efter hver enkelt, med de øvrige variable fasthol Definitionen er f(x, y) x f(x, y) f(x +
MM502+4 forelæsningsslides. uge 6, 2009
 MM502+4 forelæsningsslides uge 6, 2009 1 Definition partielle afledede: De (første) partielle afledede af en funktion f(x, y) af to variable er f(x + h, y) f(x, y) f 1 (x, y) := lim h 0 h f(x, y + k) f(x,
MM502+4 forelæsningsslides uge 6, 2009 1 Definition partielle afledede: De (første) partielle afledede af en funktion f(x, y) af to variable er f(x + h, y) f(x, y) f 1 (x, y) := lim h 0 h f(x, y + k) f(x,
Vektoranalyse INDLEDNING. Indhold. 1 Integraltricks. Jens Kusk Block Jacobsen 21. januar 2008
 Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
Vektoranalyse Jens Kusk Block Jacobsen 21. januar 2008 INLENING ette er en opsamling af ting, jeg synes er gode at have ifbm vektoranalyse som præsenteret i kurset VEKANAE07 ved IMF på AU. Noten er dels
STEEN MARKVORSEN DTU MATEMATIK
 STEEN MARKVORSEN DTU MATEMATIK 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................ 6 1.2 Approksimerende summer og
STEEN MARKVORSEN DTU MATEMATIK 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................ 6 1.2 Approksimerende summer og
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 3. fjerdedel
 MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
MATEMATIK Eksamensopgaver Juni 995 Juni 200, 3. fjerdedel August 998 Opgave. Lad f : R \ {0} R betegne funktionen givet ved f(x) = ex x for x 0. (a) Find eventuelle lokale maksimums- og minimumspunkter
Matematik F2 Opgavesæt 2
 Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
Opgaver uge 2 I denne uge kigger vi nærmere på Cauchy-Riemann betingelserne, potensrækker, konvergenskriterier og flertydige funktioner. Vi skal også se på integration langs en ve i den komplekse plan.
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 17. oktober, 2013 1 Partielle differentialligninger 1.1 D Alemberts løsning af bølgeligningen [Bogens sektion 12.4 på side 553]
MASO Uge 7. Differentiable funktioner. Jesper Michael Møller. Uge 7. Formålet med MASO. Department of Mathematics University of Copenhagen
 MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner f : R R En funktion f : R R er differentiabel
MASO Uge 7 Differentiable funktioner Jesper Michael Møller Department of Mathematics University of Copenhagen Uge 7 Formålet med MASO Oversigt Differentiable funktioner f : R R En funktion f : R R er differentiabel
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Delmængder af Rummet
 Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
af koblede differentialligninger (se Apostol Bind II, s 229ff) 3. En n te ordens differentialligning
 EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
EKSISTENS- OG ENTYDIGHEDSSÆTNINGEN Vi vil nu bevise eksistens- og entydighedssætningen for ordinære differentialligninger. For overskuelighedens skyld vil vi indskrænke os til at undersøge een 1. ordens
GEOMETRI-TØ, UGE 6. . x 1 x 1. = x 1 x 2. x 2. k f
 GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
GEOMETRI-TØ, UGE 6 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1 Lad f : R 2 R være tre gange kontinuert differentierbar
Taylorudvikling I. 1 Taylorpolynomier. Preben Alsholm 3. november Definition af Taylorpolynomium
 Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Integration i flere Variable. Steen Markvorsen Institut for Matematik, DTU
 Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 20. februar 2008 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.2 Approksimerende summer
Integration i flere Variable Steen Markvorsen Institut for Matematik, DTU 20. februar 2008 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.2 Approksimerende summer
GEOMETRI-TØ, UGE 12. A σ (R) = A f σ (f(r))
 GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
GEOMETRI-TØ, UGE 12 Hvis I falder over tryk- eller regne-fejl i nedenstående, må I meget gerne sende rettelser til fuglede@imfaudk Opvarmningsopgave 1, [P] 632 Vis at Ennepers flade σ(u, v) = ( u u 3 /3
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Matematik A 5 timers skriftlig prøve
 Højere Teknisk Eksamen august 2009 HTX092-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 28. august 2009 kl. 9.00-14.00 Side 1 af 9 sider Matematik A 2009 Prøvens varighed
Højere Teknisk Eksamen august 2009 HTX092-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 28. august 2009 kl. 9.00-14.00 Side 1 af 9 sider Matematik A 2009 Prøvens varighed
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Lidt om plane kurver og geometrisk kontinuitet
 Lidt om plane kurver og geometrisk kontinuitet Jesper Møller og Rasmus P. Waagepetersen, Institut for Matematiske Fag, Aalborg Universitet September 3, 2003 1 Indledning Dette notesæt giver en oversigt
Lidt om plane kurver og geometrisk kontinuitet Jesper Møller og Rasmus P. Waagepetersen, Institut for Matematiske Fag, Aalborg Universitet September 3, 2003 1 Indledning Dette notesæt giver en oversigt
MATEMATIK A-NIVEAU-Net Forberedelsesmateriale
 STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec.
 Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
Noter om Komplekse Vektorrum, Funktionsrum og Differentialligninger LinAlg 2004/05-Version af 16. Dec. 1 Komplekse vektorrum I defininitionen af vektorrum i Afsnit 4.1 i Niels Vigand Pedersen Lineær Algebra
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A. Studentereksamen. Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet
 Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Om første og anden fundamentalform
 Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
Geometri, foråret 2005 Jørgen Larsen 9. marts 2005 Om første og anden fundamentalform 1 Tangentrummet; første fundamentalform Vi betragter en flade S parametriseret med σ. Lad P = σu 0, v 0 være et punkt
STEEN MARKVORSEN DTU COMPUTE 2016
 STEEN MARKVORSEN DTU COMPUTE 2016 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
STEEN MARKVORSEN DTU COMPUTE 2016 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
Vektorer og lineær regression
 Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder.
 2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
2. Matematiske hjælpemidler. Koordinater. 2.1 De mange bredder. 2.1 I Figur 1.1 i kapitel 1 er der vist et ideelt Kartesiske eller Euklidiske koordinatsystem, med koordinater ( X, Y, Z) = ( X 1, X 2, X
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
STEEN MARKVORSEN DTU COMPUTE 2017
 STEEN MARKVORSEN DTU COMPUTE 2017 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
STEEN MARKVORSEN DTU COMPUTE 2017 2 Indhold 1 Regulære flader i rummet 5 1.1 Det sædvanlige koordinatsystem i rummet..................... 5 1.2 Graf-flader for funktioner af to variable......................
Supplerende opgaver. 0. Opgaver til første uge. SO 1. MatGeo
 SO 1 Supplerende opgaver De efterfølgende opgaver er supplerende opgaver til brug for undervisningen i Matematik for geologer. De er forfattet af Hans Jørgen Beck. Opgaverne falder i fire samlinger: Den
SO 1 Supplerende opgaver De efterfølgende opgaver er supplerende opgaver til brug for undervisningen i Matematik for geologer. De er forfattet af Hans Jørgen Beck. Opgaverne falder i fire samlinger: Den
Vektorer og lineær regression. Peter Harremoës Niels Brock
 Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Notesæt - Eksempler på polær integration
 Notesæt - Eksempler på polær integration Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument forsøger blot at forklare,
Notesæt - Eksempler på polær integration Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument forsøger blot at forklare,
Sætning (Kædereglen) For f(u), u = g(x) differentiable er den sammensatte funktion F = f g differentiabel med
 Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Oversigt [S] 3.5, 11.5 Nøgleord og begreber Kædereglen i en variabel Kædereglen to variable Test kædereglen Kædereglen i tre eller flere variable Jacobimatricen Kædereglen på matrixform Test matrixform
Vektorfunktioner. (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium
 Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Vektorfunktioner (Parameterkurver) x-klasserne Gammel Hellerup Gymnasium Indholdsfortegnelse VEKTORFUNKTIONER... Centrale begreber... Cirkler... 5 Epicykler... 7 Snurretoppen... 9 Ellipser... 1 Parabler...
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Integration i flere Variable. Steen Markvorsen DTU Matematik
 Integration i flere Variable Steen Markvorsen DTU Matematik 20. februar 2009 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................
Integration i flere Variable Steen Markvorsen DTU Matematik 20. februar 2009 2 Indhold 1 Introduktion 5 1.1 Hvad handler det om?................................ 6 1.1.1 Rumfang-problemet............................
Funktioner af flere variable
 Funktioner af flere variable Stud. Scient. Martin Sparre Københavns Universitet 23-10-2006 Definition 1 (Definition af en funktion af flere variable). En funktion af n variable defineret på en delmængde,
Funktioner af flere variable Stud. Scient. Martin Sparre Københavns Universitet 23-10-2006 Definition 1 (Definition af en funktion af flere variable). En funktion af n variable defineret på en delmængde,
Bevægelsens Geometri
 Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Bevægelsens Geometri Vi vil betragte bevægelsen af et punkt. Dette punkt kan f.eks. være tyngdepunktet af en flue, et menneske, et molekyle, en galakse eller hvad man nu ellers har lyst til at beskrive.
Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev)
 Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev) https://en.wikipedia.org/wiki/quadric#euclidean_space Ligning og parametrisering https://en.wikipedia.org/wiki/hyperboloid
Cirkulær hyperboloide (snoet trætårn i Camp Adventure ved Gisselfeld Kloster v/ Haslev) https://en.wikipedia.org/wiki/quadric#euclidean_space Ligning og parametrisering https://en.wikipedia.org/wiki/hyperboloid
Matematik F Et bud på hvordan eksamenssæt løses
 Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Eksamen i Calculus Mandag den 4. juni 2012
 Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Mandag den 4. juni 212 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematik A. 5 timers skriftlig prøve. Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA. Undervisningsministeriet
 Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 29. maj 2009 kl. 9.00-14.00 Matematik A 2009 Prøvens varighed er 5 timer.
Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 29. maj 2009 kl. 9.00-14.00 Matematik A 2009 Prøvens varighed er 5 timer.
Funktion af flere variable
 Funktion af flere variable Preben Alsholm 6. oktober 2008 1 Funktion af flere variable 1.1 Punktmængder i R k : Definitioner Punktmængder i flerdimensionale rum: Definitioner q Normen af x 2 R k er kxk
Funktion af flere variable Preben Alsholm 6. oktober 2008 1 Funktion af flere variable 1.1 Punktmængder i R k : Definitioner Punktmængder i flerdimensionale rum: Definitioner q Normen af x 2 R k er kxk
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 135, 270, 60, 30.
 Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Opgaver Polære koordinater Opgave 1 Opskriv følgende vinkler i radianer 180, 90, 15, 70, 60, 0. Opgave Bestem sin π Opgave. Et punkt p i xy-planen er givet ved de kartesiske koordinater,. Bestem p s polære
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005
 SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
SUPPLERENDE OPGAVER TIL KOMPLEKS FUNKTIONSTEORI F2005 0. maj, 2005 version nr. 8 JØRGEN VESTERSTRØM Indledende bemærkninger De foreliggende opgaver udgør et supplement til lærebogens opgaver. Afsnitsnummereringerne
Lokalt ekstremum DiploMat 01905
 Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
Lokalt ekstremum DiploMat 0905 Preben Alsholm Institut for Matematik, DTU 6. oktober 00 De nition Et stationært punkt for en funktion af ere variable f vil i disse noter blive kaldt et egentligt saddelpunkt,
INERTIMOMENT for stive legemer
 Projekt: INERTIMOMENT for stive legemer Formålet med projektet er at træne integralregning og samtidig se en ikke-triviel anvendelse i fysik. 0. Definition af inertimoment Inertimomentet angives med bogstavet
Projekt: INERTIMOMENT for stive legemer Formålet med projektet er at træne integralregning og samtidig se en ikke-triviel anvendelse i fysik. 0. Definition af inertimoment Inertimomentet angives med bogstavet
En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby
 24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
Kalkulus 2 - Grænseovergange, Kontinuitet og Følger
 Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
Kalkulus - Grænseovergange, Kontinuitet og Følger Mads Friis 8. januar 05 Indhold Grundlæggende uligheder Grænseovergange 3 3 Kontinuitet 9 4 Følger 0 5 Perspektivering 4 Grundlæggende uligheder Sætning
