SØREN L. BUHL KOMPLEKSE TAL M. M. Matematik 1 Den teknisk naturvidenskabelige Basisuddannelse

Transkript

1 SØREN L. BUHL KOMPLEKSE TAL M. M. Matematik Den teknisk naturvidenskabelige Basisuddannelse Afdeling for Matematik og Datalogi Institut for Elektroniske Systemer Aalborg Universitetscenter MCMXCII

2 Indhold 0 Indledning Polære koordinater 3 Komplekse tal på cartesisk form 3 Komplekse tal på polær form 7 4 Det komplekse andengradspolynomium 5 Det komplekse polynomium af n te grad 6 6 Den komplekse eksponentialfunktion 30 7 Homogene lineære differentialligninger 33 8 Inhomogene lineære differentialligninger 46

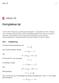
3 Directionen af alle Linier i samme Plan kan udtrykkes ligesaa analytisk, som deres Længde, uden at Hukommelsen bebyrdes med nye Tegn eller Regler. Caspar Wessel (745 88) i Om Directionens analytiske Betegning Han tegner Landkort og læser Loven. Han er saa flittig som jeg er Doven. Johan Herman Wessel om sin broder. 0 Indledning Dette notat er beregnet til brug ved kurset Matematik under AUC s teknisknaturvidenskabelige basisuddannelse. Det har som sit hovedemne indførelsen af de komplekse tal. Der introduceres først polære koordinater i planen, for at den polære form af komplekse tal lettere kan behandles. Den komplekse eksponentialfunktion benyttes til løsning af homogene og inhomogene lineære differentialligninger med konstante koefficienter. Hvert afsnit afsluttes med en opgavesamling. Notatet afsluttes med en facitliste. Her skal anføres nogle resultater fra trigonometrien, som vi får brug for senere. Først en lille tabel: u 0 6 π 4 π 3 π π grader 0 o 30 o 45 o 60 o 90 o sinu 0 3 cosu 3 0 tanu () Der findes mange formler for vinkelskift, men frem for at bruge formelsamling anser jeg det for bedre at udlede disse formler, når man får brug for dem, ved at se på en enhedscirkel. Vi minder om den fra gymnasiet kendte cosinusrelation, Disse citater har jeg hentet fra Kirsti Møller Pedersen: Caspar Wessel og de komplekse tals repræsentation. Nordisk Matematisk Tidsskrift, 979, hefte. Caspar Wessel var den første, der opfattede komplekse tal som punkter i planen.

4 Komplekse tal m. m. der for en trekant med en vinkel C afgrænset af siderne a og b og med c som modstående side udsiger, at c a b abcosc () Endvidere får vi brug for de såkaldte additionsformler for cosinus og sinus. De lyder: cos u v cos u v sin u v sin u v cosucosv sinusinv cosucosv sinusinv sinucosv cosusinv sinucosv cosusinv For at bevise dem starter vi med at indføre følgende vektorer i : a a a cosu sinu b b b cosv sinv (3) For deres skalarprodukt har vi to udtryk: a b a b cosθ a b a b hvoraf den første formel i (3) fås, da der er tale om enhedsvektorer med θ u v. Ved at erstatte v med v får vi den næste formel. I denne erstattes u med π u, og vi får den tredje formel. Og heri erstatter vi v med v for at få den sidste formel. OPGAVER 0.. Vis rigtigheden af tallene i (), fx ved at se på retvinklede trekanter. 0.. Udled formlerne sinx sinxcosx cosx cos x sin x cos x sin x 0.3. Udled formlerne cosx cosx sinx hvor fortegnet afhænger af den kvadrant, som x ligger i. cosx 0.4. Vis, at tanx tanx tan x

5 . Polære koordinater Der er andre trigonometriske additionsformler end de i teksten viste. Udled følgende nyttige formler ud fra (3): cosu cosv cos u v cosu cosv sin u v sinu sinv sinu sinv sin u v cos u v cos u v sin u v cos u v sin u v 0.6. Benyt den foregående opgave til at finde ud af, hvad der sker, når man superponerer to vekselstrømme med samme amplitude og med næsten samme frekvens. (Stående bølger.) Polære koordinater I planen indføres et koordinatsystem O e, e, hvor O er origo og e, e på hinanden ortogonale enhedsvektorer, hvor den korteste drejning fra e til e er i positiv omløbsretning (mod uret). For et punkt P har vi de sædvanlige, såkaldt cartesiske koordinater x y, hvor abscissen x og ordinaten y er definerede ud fra stedvektoren ved OP xe ye. Endvidere er punktet P bestemt ud fra stedvektorens længde r OP og vinklen θ, der angiver drejningen fra e til OP, regnet med fortegn. Vi kalder r og θ punktets polære koordinater og skriver x y r θ pol Vi kalder r radiusvektor og θ retningsvinkel. Der gælder, at r 0. Medens radiusvektor derved er entydigt bestemt, gælder dette ikke retningsvinklen: Ved addition af et helt multiplum af π fås det samme punkt, så alle værdier θ πk, k, kan benyttes. 3 For origo, altså r 0, er θ helt ubestemt. Halvlinien ud fra origo i abscisseaksens positive retning kaldes polaraksen. På figur vises de cartesiske og de polære koordinater for punktet P. Af simple trigonometriske formler får man og x r cosθ y r sinθ (4) r x y tanθ y x (5) Efter René Descartes ( ), der på latin kaldte sig Cartesius. 3 betegner mængden af hele tal.

6 4 Komplekse tal m. m. " y P (x,y) # r 0! x Figur : Polære koordinater Formel (4) angiver entydigt overgangen fra polære til cartesiske koordinater. Derimod angiver (5) kun radiusvektor entydigt ved den modsatte overgang. Dels til- 0 en løsning, lader formlen for retningsvinklen θ ikke, at x 0, dels er der for x $ hvor π % θ % π, og den er falsk, hvis punktet ligger i. eller 3. kvadrant; så skal π adderes (eller subtraheres). Derfor skal man altid se på, hvilken kvadrant punktet ligger i. 4 Som en øvelse kan læseren dobbeltchecke ligningerne 0 = 0 pol 0 = π pol = & 3 = π 4 pol π 3 pol ved at verificere dem både forlæns og baglæns. Vi skal se på en række eksempler på, hvordan en kurve kan beskrives i polære koordinater. Specielt beskriver ligningen r a en cirkel med centrum i origo og radius a. Ligningen θ α beskriver en halvlinie ud fra origo (stråle), der er drejet vinklen α ud fra polaraksen. I de tilfælde, hvor en stråle højst skærer kurven én gang, kan vi beskrive kurven ved en ligning af formen r g θ. Man skal her være opmærksom på, at man kun må bruge θ-værdier, for hvilke r 0. 5 En kurve er symmetrisk omkring x-aksen, hvis ligningen bliver uforandret, når θ erstattes 4 Mange lommeregnere kan direkte konvertere mellem ' x( y) og ' r( θ) pol. 5 Nogle lærebogsforfattere tillader negative r, så '+* r( θ) pol, ' r( θ * π) pol. Herved kan nogle

7 . Polære koordinater 5. A P - O 0 C Figur : Cirkel gennem origo af θ. Den er symmetrisk om y-aksen, hvis ligningen bliver uforandret, når θ erstattes af π θ. Den er symmetrisk om origo, hvis ligningen bliver uforandret, når θ erstattes af θ π. EKSEMPEL. En ret linie har i cartesiske koordinater ligningen x y polære koordinater.. Find dens ligning i Løsning: Ved brug af (4) fås r cosθ r sinθ. Tegn linien for at få θ-intervallet! Man får r cosθ sinθ 4 π % θ % 3 4 π Man finder i øvrigt en symmetri, der ikke er omtalt ovenfor: Hvis θ erstattes af π θ, bliver r uforandret, da sinus og cosinus byttes om; derfor er der symmetri om linien y x, i polære kordinater strålen θ 4 π. / EKSEMPEL. Find i polære koordinater ligningen for cirklen med centrum i a 0 og radius a. smukke sløjfer beskrives simplere. Til gengæld er det vanskeligere at undersøge, hvornår to sæt polære koordinater bestemmer det samme punkt.

8 6 Komplekse tal m. m. Løsning: Af fig. ses, at r 0 OP OA OC cosθ. Da figuren ligger i. og 4. kvadrant, fås r acosθ π θ π Symmetrien omkring x-aksen aflæses af, at udtrykket (og θ-intervallet) ikke ændres, når θ skifter fortegn. / Antag, at en kurve med ligningen r g θ drejes en vinkel α omkring origo. Herved vil punktet P med r θ pol blive drejet over i punktet P med r θ α pol. For at P s polære koordinater kan passe i ligningen, må vi trække vinklen α fra. Vi har følgende resultat: g θ drejes vinklen α, regnet med fortegn, så får den nye kurve ligningen r g θ α. Hvis en kurve med ligningen r EKSEMPEL.3 Hvilken kurve beskrives ved r sinθ, 0 θ π? Løsning: Udtrykket kan omskrives til r cos θ π. Af eksempel. med a ses, at der er tale om en en cirkel med centrum 0 og radius. / Vi skal nu se nogle eksempler på kurver, der beskrives i polære koordinater. Ved kurvetegningen skal man især være opmærksom på, hvornår r 0, og om der θ-værdier, der skal udelukkes, fordi r er negativ. Støttepunkter plottes ved, at man for udvalgte θ-værdier afsætter den tilsvarende r-værdi ud ad strålen. I en del af tilfældene er r uforandret, når π adderes til θ. I så fald et det nok at angive et θ-interval af længde π, fx π % θ π eller 0 θ % π. EKSEMPEL.4 Skitsér kurven med ligningen r cosθ. (Den kaldes kardioiden.) Løsning: (Se fig. 3) Vi ser, at radiusvektor vokser fra 0 til, når retningsvinklen vokser fra 0 til π, og aftager fra til 0, når retningsvinklen vokser fra π til π. Da udtrykket ikke ændres, når θ erstattes af π θ (eller skifter fortegn), er der symmetri omkring x-aksen. Her er nogle støttepunkter: θ π 3 3 π 3 π 3 3 π π π r Disse værdier kan omregnes til decimalbrøk og evt. konverteres til cartesiske koordinater på en lommeregner. Omkring θ 0 går kurven direkte ud fra origo, og vi får en såkaldt spids. Dette svarer til, at der er to halvtangenter, der er ensrettede. (For almindelige tangenter er de modsat rettede.) Navnet kardioide skyldes hjerteformen. / (6)

9 . Polære koordinater 7 Figur 3: Kardioide EKSEMPEL.5 Vis, at r cosθ beskriver en firebladet rose. Løsning: (Se fig. 4) Der er spidser for r 0, hvilket indtræffer for θ π, 3 4 π. Et enkelt blad fås for 4 π θ 4 π, hvor r antager sin maksimale værdi for θ 0. Af (6) ses, at de andre blade fås ved at dreje et helt multiplum af π (se fig. 4). Hvis numerisktegnet fjernedes, altså r cosθ, ville man kun få to blade, da r % 0 for 3 4 π θ 4 4 π og 4 π θ 3 4 π. (Med kurvetegningsprogrammer, der tillader negative r, ville man stadig få alle fire blade.) / EKSEMPEL.6 (Archimedes spiral.) Skitsér kurven givet ved ligningen r θ. Løsning: (Se fig. 5) Defineret for θ 0. r vokser jævnt som funktion af θ og forøges med π for hver omdrejning. / EKSEMPEL.7 Der er givet en ellipse med halvakser a og b a e, hvor e er excentriciteten. De to brændpunkter er hhv. i origo og modsat rettet polaraksen. Find ellipsens ligning i polære koordinater.

10 8 Komplekse tal m. m. Figur 4: Firebladet rose Figur 5: Archimedes spiral

11 -. Polære koordinater 9 P F # r 5 0 O Figur 6: Ellipse Løsning: (Se fig. 6) Lad P være et vilkårligt punkt på ellipsen, og lad brændpunkterne være O og F. Af cosinusrelationen () fås FP OP 6 FO OP 7 FO cos π θ som, da ellipsen er defineret ved FP 84 OP ea, bliver til der efter reduktion kan omformes til a r r 4e a 4reacosθ a, og brændpunktsafstanden er r a e ecosθ / Ved forskellige anvendelser, fx arealberegning, har man brug for at finde skæringspunkterne mellem kurver beskrevne i polære koordinater. Her er der et problem, som man ikke har for cartesiske koordinater, nemlig at flere værdier af θ giver samme punkt. EKSEMPEL.8 Find skæringspunkterne mellem kardioiden r sinθ og cirklen r 3sinθ. Løsning: (Se fig. 7) Idet sinθ cos θ π, er kardioiden drejet π ud fra den i eksempel.4. På nær faktoren 3 er cirklen den i eksempel.3 nævnte. Vi sætter sinθ 3sinθ og får sinθ med løsninger θ 6 π, 5 6π. Herved fås

12 0 Komplekse tal m. m. Figur 7: Kardioide og cirkel 3 skæringspunkterne π pol og π 3 6 pol eller i cartesiske koordinater og & Da begge kurver går gennem origo, er dette også et fællespunkt, selv om man i ligningerne ikke får r 0 for de samme θ-værdier. Det er klogt altid at lave en skitse, da man ellers let kan overse nogle skæringspunkter. / EKSEMPEL.9 Find skæringspunkterne mellem Archimedes spiral r θ og strålen θ π. Løsning: Det er ikke nok at indsætte θ π i r θ, da addition af π giver samme retningsvinkel. (Tegn!) Vi må altså indsætte θ π kπ, k (Ingen negative θ, da θ 0 for spiralen.) Endvidere er origo fællespunkt, altså origo eller på cartesisk form π π 5 pol π π 0 π 9 pol π 5 π 0 π pol : 9 9 π 9 : / 3 4 OPGAVER.. Angiv polære koordinater for følgende punkter: (a) ; 0< =, (b) ; =, (c) ;?> 3< =, (d) ;@A> 3< 3=, (e) ;@ > 6 > =.

13 . Polære koordinater.. Nedenstående punkter er sammenfaldende to og to på nær to umage. Find sammenhængen. (a) ; π= pol, (b) ; 0 = pol, (c) ; 3 3 π= pol, (d) ; < 7π= pol, ; ; ; ; ; ; (e) 0= pol, (f) 3< 3 pol, (g) 0 π= pol, 8 (h) 3 3 pol, (i) 3 3 pol, (j) π= pol. Angiv en ligning i cartesiske koordinater for hver af nedenstående ligninger i polære koordinater. Angiv kurvetypen..3. r cosθ 3,.4. r B sinθ..5. r sinθ..6. cos θ sin θ..7. r cosθ lnr lnsinθ. Find de cartesiske koordinater for skæringspunkterne mellem følgende kurver:.8. r og r cosθ..9. r sinθ og r BC; sin θ=,.0. r > 3cosθ og r sinθ... Skitsér grafen for r cosθ... Opstil ligningen i polære koordinater og skitsér grafen for en seksbladet rose..3. Markér hvert af de følgende udsagn som Sandt eller Falsk: a) Bortset fra når x 0, bestemmes retningsvinklen θ ved tanθ yb x. b) De polære koordinatsæt ; r θ = pol og ; r θ = pol bestemmer det samme punkt, hvis og kun hvis r r og θ θ. c) For et givet polært koordinatsæt ; r θ= pol findes der kun ét cartesisk koordinatsæt, der bestemmer det samme punkt. d) For en kurve beskrevet ved ligningen r g; θ= er det nok at se på θ i intervallet 0 D θ E π. e) Amerikanske calculusbøger tillader normalt r E 0.

14 Komplekse tal m. m..4. Skitsér grafen for r BC; cosθ=. Hvilken type kurve er det?.5. Skitsér grafen for r BC; cosθ=. Hvilken type kurve er det?.6. Lad F betegne en ret linie, der ikke går gennem origo. Lad P betegne projektionen af origo O på F. Vis, at hvis afstanden er d 6G OPG og OP 7H danner vinklen α med polaraksen, så er liniens ligning i polære koordinater r db cos; θ α=. (Vink: Geometrisk argument, eller drej linien x d og benyt (6).).7. Find ligningen i cartesiske koordinater for cirklen i eksempel.. Benyt den til at give en alternativ udledning af r acos θ..8. Udled ellipseligningen i polære koordinater fra eksempel.7 ved at indsætte i ellipsens ligning i cartesiske koordinater..9. (Lemniskaten.) Lad A I;@ 0= og B I; 0= i cartesiske koordinater. Find ligningen i polære koordinater for kurven bestående af de punkter P, for hvilke G PAG@J G PBGK. (Vink: Benyt () og opg. 0..).0. En hyperbel har halvakserne a og b a> e, hvor e er excentriciteten. Brændpunkterne er i origo og på polaraksen. Find ligningen i polære koordinater for den venstre gren af hyperblen... Lad 0 D a D. Kurven r acos θ har et antal lodrette tangenter, der afhænger af a. Find sammenhængen. (Vink: Find ; x y= som funktion af θ.).. (Logaritmisk spiral.) Vis, at kurven bestemt ved r e θ har uendelig mange vindinger. Hvor mange vindinger kan man praktisk vise på en figur? (Tegn!) Komplekse tal på cartesisk form De første tal, man lærer om, er de naturlige tal, altså mængden L NM PO. De tre prikker fortæller, at der ikke er noget største tal, og mere præcist udtrykkes dette ved induktionsaksiomet. L er lukket over for addition og multiplikation. For altid at gøre subtraktion mulig udvider man til mængden QM : &O af hele tal. Divisionen får man med (på nær division med nul) i mængden R af rationale tal. Differential- og integralregning kræver, at grænseovergang er mulig, og hertil behøver man mængden af reelle tal. Men stadig er der polynomier, der ikke har rødder, fx x. For at løse dette problem indfører man mængden S af komplekse tal, der omfatter alle talpar z x y, hvor x y. Vi kalder x den reelle del og y den imaginære del, og skriver x Re z, y Im z. Ofte afbilder man z x y i planen på samme måde som en vektor i og taler om den komplekse plan med den

15 . Komplekse tal på cartesisk form 3 0, siges z at være imaginær. Hvis reelle og den imaginære akse. 6 Hvis Im z T$ yderligere Re z 0, siges z at være rent imaginær. Vi indfører addition og multiplikation af to komplekse tal a a a og b b b ved a b a a b b a b a b (7) ab a a U b b a b a b a b a b V (8) Hvis den imaginære del er nul, får man a 0 b 0 a b 0 a 0 U b 0 a b 0 hvilket berettiger os til at identificere sådanne komplekse tal med de reelle tal, da der er isomorfi mht. addition og multiplikation. Vi skriver derfor x 0 x. Specielt er Det ses umiddelbart ved ombytninger i (7) og (8), at den kommutative lov gælder såvel for addition som for multiplikation, altså a b b a ab ba Også den associative lov gælder for begge regningsarter, altså a b c a b c ab c a bc V For addition fås loven umiddelbart, da den gælder for de to dele hver for sig. For multiplikation overlades beviset til læseren (opg.6). Endvidere gælder den distributive lov a b c ab ac som vi nu vil bevise: a b c a a 9 b b c c : a a b c b c a b c W a b c a b c a b c 9 a b a b a b a b a c a c a c a c ab ac Da additionen foregår for hver del for sig, gælder dette også subtraktionen. Hvad angår division, skal vi for a $ 0 løse ligningen az b X a a x y b b 6 Kaldes ofte et Argand-diagram efter svejtseren Jean Robert Argand, selv om nordmanden Caspar Wessel var den første, der fandt på det. Men han publicerede på dansk!

16 4 Komplekse tal m. m. der vha. (8) omformes til ligningssystemet a x a y a x a y der har præcis én løsning, da determinanten er a a, som er ikke er nul pga. forbeholdet a $ 0. For løsningen z x y skrives z by a. b b EKSEMPEL. Lad a og b & 3. Find a b, b a, ab og by a. Løsning: Vi får a b 0 5, b a &, ab & 7, by a. (Opstil og løs ligningssystemet (9) svarende til divisionen!) / Det viser sig, at man kan undgå talparnotationen, hvis man indfører den såkaldt imaginære enhed i 0 Af (8) ses, at i. Hermed får vi, at polynomiet z har roden z i. (z i er den anden rod.) Vi har nu for x y Z Vi vil kalde begge skrivemåder, altså x iy x 0 0 U y 0 x y z x y x iy cartesisk form; i det følgende bruges sædvanligvis den sidste. Man behøver ikke at huske (8) for at kunne multiplicere, kun at i. For tallene i eksempel. fås ab i U & 3i 3i i 6i 7 i For at lette divisionen indfører vi svarende til z x iy den komplekst konjugerede z x iy. Geometrisk svarer kompleks konjugering til spejling omkring den reelle akse. Det er let at vise følgende egenskaber ved kompleks konjugering: (9) a b a b a b a b ab ab ay b ay b a a (0) Vi overlader påvisningen til læseren (opg..7) på nær for den midterste, for hvilken beviset ser således ud: ab a ia U b ib a b a b i a b a b a b a b [ i a b a b a ia U b ib ab

17 /. Komplekse tal på cartesisk form 5 Længden af z x iy, opfattet som en vektor i, kaldes modulus (eller numerisk værdi) og betegnes z. Vi har z zz x y Vi er nu i stand til at beregne brøken by a på en simplere måde end ved at løse ligningssystemet (9). Vi forlænger brøken med den komplekst konjugerede til nævneren. Da b ba ba a aa a får reel nævner, er det let at finde den reelle del og den imaginære del af brøken. Vi illustrerer med et eksempel: EKSEMPEL. Beregn by a for tallene i eksempel. ved brug af kompleks konjugering. Løsning: b 3i a & 3i U i i i 5 5i 5 i Sammenfattende kan man sige, at man regner med komplekse tal på samme måde som med relle tal, idet man benytter den ekstra regel i og forlænger brøker med den komplekst konjugerede til nævneren. Der er dog en undta- z, medmindre z er reel gelse, nemlig reglen x x. Faktisk gælder altid z $ (opg..8). OPGAVER Angiv følgende udtryk på cartesisk form ; dvs. a ib= :.. ; i=\]; 3 4i=... ; 3i=9;@ 5i=..3. i ; i=9; 3 i=9; i=9; 3 i= i. 7 7i 3i.

18 6 Komplekse tal m. m ; 3 43i=9; 75 6i= ; 6 75i=9; 43 3i= > 3 i> > i> 3.. Afbild nedenstående mængder af z-værdier i den komplekse plan..9. G zgue E^G zgue... G z igu_... G z igk`g z ig..3. Re a z 3 i b G zg Re; z= Im; z=[ Markér hvert af de følgende udsagn som Sandt eller Falsk: a) Komplekse tal z ced er det samme som talpar ; x y=fctg. b) Én af egenskaberne ved komplekse tal er, at de kan opfattes som talpar ; x y=hctg. c) Man kan ikke dividere med et komplekst tal z i; x y=, hvis én af delene x eller y er lig nul. d) Man kan dividere med et komplekst tal z ; x y=, medmindre begge delene x og y er lig nul. e) Hvis z j z, så er z rent imaginær..6. Vis, at den associative lov for multiplikation af komplekse tal gælder, altså a; bc=k ; ab= c..7. Vis, at formlerne (0) for kompleks konjugering gælder..8. Vis, at for komplekse tal gælder G z GK z, hvis og kun hvis z clg..9. Udled trekantsuligheden for komplekse tal: m m m G z G<nG z G m DoG z z GUDpG z GqG z Gsr (Vink: Benyt, at en side i en trekant er mindre end summen af de to andre og større end deres differens.) Hvornår kan der være lighedstegn?

19 3. Komplekse tal på polær form 7 3 Komplekse tal på polær form Det komplekse tal z x iy har, opfattet som et punkt x y i den komplekse plan, naturligvis også polære koordinater. Vi siger, at z r θ pol er den polære form af tallet. Sammenhængen med den cartesiske form er givet ved Vi skriver z r cosθ isinθ V () r z θ arg z hvor z er den tidligere indførte modulus og arg z kaldes argument. Man kalder også den polære form for modulus-argument-form. Argumentet arg z er kun defineret på nær et helt multiplum af π. (For z 0 er det helt udefineret.) Ved hovedargumentet forstås den retningsvinkel θ Arg z, for hvilken π % Arg(z) π. EKSEMPEL 3. Angiv z i på polær form. Løsning: Modulus er z K, og for argumentet fås tanθ. Da z er i. kvadrant, vælges θ 3 4 π. Vi får z 3 π 4 pol. (Tegn!) / Den polære form er ikke meget bevendt ved addition og subtraktion. Derimod er den nyttig ved multiplikation og division. Lad Vi har da z x iy r θ pol z x iy r θ pol z z r cosθ isinθ r cosθ isinθ r r : cosθ cosθ sinθ sinθ i cosθ sinθ sinθ cosθ 9 r r cos θ θ isin θ θ 9 r r θ θ pol hvor vi har benyttet to af additionsformlerne i (3). Vi har altså Udtrykt som en regel har vi: z z z t z arg z z arg z arg z ()

20 v v v v v v v 8 Komplekse tal m. m. Im uz=x+iy z arg(z) Figur 8: Et komplekst tal Re Ved multiplikation af komplekse tal multiplicerer man deres moduli og adderer deres argumenter. (3) Man bør være opmærksom flertydigheden i argumenterne. Hvis man for z og z angiver hovedargumenterne, kan man ikke være sikker på, at man ved addition får hovedargumentet for z z. (Overvej dette!) For divisionen gælder, at w z Y z er løsningen til ligningen z w z. Derfor fås af (): v z z z z z arg w arg z W arg z (4) z x EKSEMPEL 3. Lad z 3 i, z i 3. Beregn z z og z Y z ved at benytte polær form. Løsning: Vi har og får derfor af () z z z π 6 pol z 4 z z 3 π pol 5 6 π pol 3 i π pol i

21 3. Komplekse tal på polær form 9 Resultatet kan også fås ved at benytte cartesisk form. 7 / Multiplikationsreglen (3) er formuleret for et vilkårligt antal faktorer, selv om vi formelt kun har vist den for to faktorer. At z z 9 9 z n z t z 9 9 z n arg z z 9 9 z n arg z arg z :9 arg z n gælder for alle n yl, fås let ved et induktionsbevis. Er alle z erne ens, får vi potensreglen z nv z n arg z n narg z (5) der for z $ 0 kan vises at gælde for alle n Z. EKSEMPEL 3.3 Beregn i 3 3. Løsning: Udtrykket kan naturligvis beregnes direkte. Vi vil i stedet benytte polær 3. Da z form. For z i 3 er modulus z V, og for argumentet fås tanθ er i. kvadrant, bruges θ 3 π. Vi får z 3 π pol. Derfor er z 3 8 π 8. / Specielt har man for z z, altså for tal på den komplekse enhedscirkel, at z θ pol cosθ isinθ og heraf z n nθ pol cosnθ isinnθ, altså har vi vist de Moivres formel 8 : EKSEMPEL 3.4 Udled formler for cos3θ og sin3θ. Løsning: Ved brug af (6) fås cosnθ isinnθ cosθ isinθ n (6) cos3θ isin3θ cosθ isinθ 3 cos 3 θ 3icos θsinθ 3i cosθsin θ i 3 sin 3 θ 4M cos 3 θ 3cosθ cos θ VO i M 3 sin θ sinθ sin 3 θo 4cos 3 θ 3cosθ i 3sinθ 4sin 3 θ Da realdelen og imaginærdelen stemmer overens, får vi formlerne cos3θ 4cos 3 θ 3cosθ sin3θ 3sinθ 4sin 3 θ / 7 Dette eksempel overbeviser dig måske ikke om fordelene ved den polære form; men vent til du kommer til den binome ligning! 8 Abraham de Moivre ( ). Omtrentlig udtale: dø mu-{ a-vrø, ø som i gøre.

22 0 Komplekse tal m. m. Vi skal nu se på hvordan man løser den såkaldte binome ligning: hvor w er et givet komplekst tal. Vi ser bort fra det trivielle tilfælde w z n w 0, hvor kun z 0 er løsning. Idet vi sætter w r θ pol, skal vi finde z s ϕ pol. Vi får s n nϕ pol r θ pol Da modulus er entydigt bestemt, fås s n r. Derimod er argumentet kun bestemt på nær et helt multiplum af π, så vi får nϕ θ πk k ] og dermed ϕ θ π n n k k ]T Vi får forskellige placeringer i den komplekse plan for k 0 9 : n, hvorefter der er periodisk gentagelse. De forskellige løsninger er derfor z w r n θ π n n k k 0 9 : n (7) x pol De n løsninger ligger i den komplekse plan som vinkelspidserne i en regulær n- kant. Vi vil kalde alle løsningerne n-terødder af w. EKSEMPEL 3.5 Find de tre tredjerødder af 8i. Løsning: Idet z 3 8i 8 eller i cartesiske koordinater π pol, er løsningerne i z: π 6 pol 5 π 6 pol 3 i 3 i i 3 π pol Rødderne udgør vinkelspidserne af en ensvinklet trekant (se fig. 9). /

23 w 3. Komplekse tal på polær form Im Re Figur 9: De tre tredjerødder af i EKSEMPEL 3.6 Find de seks sjetterødder af 64, og angiv dem på cartesisk form. Løsning: På polær form er π pol, hvorfor z 6 64 har løsningerne z 6 64 π πk 6 x pol 6 π k 3 π pol k De ligger alle på en cirkel med radius og centrum i 0. Argumenterne er 6 π, π, 5 6 π, 6 7π, 3 π, 6 π. På cartesisk form er rødderne med en sammentrængt skrivemåde z 3 i i. Du er ikke færdig med dette eksempel, før du har indtegnet rødderne i den komplekse plan. / OPGAVER 3.. Angiv den polære form for følgende komplekse tal: (a) i, (b) i, (c) > 3 i, (d) A> 3 3i, (e) > 6 i>. 3.. Konvertér følgende polære former til cartesiske former: (a) ; < 4 π= pol, (b) ; 0 = pol, (c) ; 5 5π= pol, (d) ; > 3 4 π= pol, (e) ; 00 3 π= pol.

24 Komplekse tal m. m Løs ligningen z 4 j Løs ligningen z 4 j 8 8> 3i Løs ligningen ; z = Løs ligningen ; z = 3 j Find ; > 3 = Find ; i= Markér hvert af de følgende udsagn som Sandt eller Falsk: a) For alle z er hovedargumentet Arg; z= entydigt bestemt. b) For alle z } 0 er hovedargumentet Arg; z= entydigt bestemt. c) Der er en simpel formel for addition af komplekse tal på polær form. d) Den polære form er velegnet ved potensopløftning og roduddragning. e) Hvis ; a ib= 3 8, så er a b For hvilke komplekse tal z er z B z? 3.. For hvilke tal z er z i. kvadrant (Re; z=fe 0, Im; z=~_ 0)? 3.. For hvilke tal z er z 3 i. kvadrant? 3.3. Lad s sin8 o. Vis, at sin54 o 3s 4s 3 cos36 o, og dermed, at s tilfredsstiller ligningen 4s 3 s 3s 0. Find sin8 o. 4 Det komplekse andengradspolynomium Vi ser først på ligningen w hvor w u iv er et komplekst tal. Ved at skrive w på polær form, altså w r θ pol, kan vi finde de to løsninger ved at tage kvadratrod af modulus og halvere argumentet (løsningen (7) til den binome ligning med n z ). Her skal gives en anden metode. For w reel, altså w u, kender vi i forvejen resultatet. For u 0 er der de reelle løsninger z 3 u, for u 0 er der én løsning z 0, og for u % 0 er der de to rent imaginære løsninger z 3 i u.

25 4. Det komplekse andengradspolynomium 3 0. Vi sætter z x iy, og da x y ixy, får vi ved at identificere reelle dele for sig og imaginære dele Vi antager dernæst, at w er imaginær, altså v $ z for sig ligningerne x y u xy v 0, må også x $ 0 og y $ Da vi antog, at v $ 0. Vi finder af den sidste ligning y vy x, som ved indsættelse i den første efter omformning giver x 4 ux v 4 0 Dette er en reel andengradsligning i x med diskriminant u v modulus for w, altså r w. Vi får x u 3 r. Da u % r (husk v $ x u r ingen løsning, idet x ikke kan være negativ. Af x u r fås r, hvor r er 0), giver og dermed ved indsættelse y 3 x v 3Z r u 3 r u v v r u hvor vi har forlænget brøken med r u og benyttet v v indfører fortegnsfunktionen (for reelle tal) sign x x x ƒ for x 0 for x % 0 r u. Vi og får, da fortegnene hører sammen, de to løsninger til z w u iv z 3 w r u i sign v r u x (8) Vi bemærker, at for v 0 kan vi også bruge formlen, hvis vi negligerer sign v, da enten den reelle eller den imaginære del forsvinder. EKSEMPEL 4. Vi ønsker at løse ligningen z 3 4i. Løsning: Da modulus er r 9 6 5, giver formel (8) z i 5 3 ƒ i i /

26 4 Komplekse tal m. m. Vi ser nu på den generelle komplekse andengradsligning az bz c hvor a, b og c er komplekse konstanter, med a $ 0. Vi benytter den samme metode som ved løsning af den reelle andengradsligning, nemlig kvadratudfyldning. Da metoden er vigtig, skal beviset gentages her. Vi sætter a uden for parentes og opfatter z som det ene kvadratled og bzy a som det dobbelte produkt. Vi udfylder med det andet kvadratled by a og får Vi indfører diskriminanten d ligningen az bz c a w z b ax 0 b 4a c b 4ac på samme måde som for reelle tal og får w z b ax d 4a Når to komplekse tal har samme kvadrat, følger det af (8), at de enten er ens eller ens med modsat fortegn, så z b 3 a d a og vi får samme løsningsformel som for den reelle andengradsligning z b 3 d a d b 4ac I modsætning til for reelle tal er d ikke veldefineret, da ligningen z d har to løsninger, hvoraf ingen særligt kan fremhæves. Dette giver dog ingen problemer her, på grund af at der står 3 i formlen. Vi ser, at vi i det komplekse tilfælde altid får to forskellige rødder, bortset fra tilfældet d 0, hvor z by a er dobbeltrod. 9 EKSEMPEL 4. Løs ligningen 3 i z o 9 3i z Egentlig burde man ikke bruge navnet diskriminant i det komplekse tilfælde, da d ikke diskriminerer mellem, om der er rødder eller ej, som i det reelle tilfælde.

27 / 4. Det komplekse andengradspolynomium 5 Løsning: Vi får d 9 3i 40 3 i 48 4i med modulus r , så d i i Derfor er løsningen z 9 3i 3` 7i 3 i Š ˆ i U 3 i i U 3 i 5 i i EKSEMPEL 4.3 Løs ligningen iz 4 i z 0 Løsning: Vi opfatter først udtrykket som en andengradsligning i z, med d i 4i i. Vi får z Œ i 3` i i For z er z 3 i, og for z i er z 3 i :Y. Vi får de fire rødder i fjerdegradspolynomiet z i i i i / Š ˆ i OPGAVER Løs følgende andengradsligninger: 4.. z 8i z 80 8i z > 3i z z z ]; i= z i z ]; i= cz ic 0, hvor c ced er givet.

28 6 Komplekse tal m. m z ; 5i= z 9 7i > 3z 9z 7> 3 3i Markér hvert af de følgende udsagn som Sandt eller Falsk: a) For komplekse tal z er kvadratroden > z veldefineret. b) En andengradsligning har altid mindst én kompleks løsning. c) En andengradsligning har altid mindst én imaginær løsning. d) En andengradsligning har altid to forskellige komplekse løsninger. e) Til løsning af ligningen z w er det i nogle tilfælde bedst at bruge formel (8), i andre tilfælde formel (7). Løs følgende ligninger og afbild løsningerne i den komplekse plan: 4.0. z 4 3z z 3 z z z 8 3z z 6 ; 8i= z 3 8i Find fejlen i følgende bevis for, at j : > Ž ;@ =9;@ = > J > i J i i j r 5 Det komplekse polynomium af n te grad Lad p z c n z n c n z n 99 c z c 0 hvor c 0 c 9 9 c n ZS og c n $ 0. For et α ZS får vi ved polynomiers division, der forløber på samme måde som for reelle polynomier, p z z α q z r hvor kvotienten q z er et polynomium af n te grad og resten r ns. Vi ser, at p α r, altså det for reelle polynomier velkendte resultat, at α er rod i p z, hvis og kun hvis z α går op i p z. Hvad angår eksistensen af rødder gælder der algebraens fundamentalsætning, der siger, at ethvert komplekst polynomium (af grad n ) har mindst én kompleks rod. 0 Hvis α er rod, går z α op, og vi kan anvende sætningen igen på 0 Først bevist i 799 af C. F. Gauss ( ).