Sekvensgrafer med TI-Nspire CAS (version 3.2)
|
|
|
- Pia Jepsen
- 8 år siden
- Visninger:
Transkript
1 Sekvensgrafer med TI-Nspire CAS (version 3.2) Indholdsfortegnelse: Eksempel 1: Hunden og haren side 1 (første ordens differensligninger) Eksempel 2: Fibonaccital side 7 (anden ordens differensligninger) Eksempel 3: Radioaktive henfaldskæder side 15 (koblede differensligninger) Eksempel 4: Feigenbaumiteration side 23 (tidsserie og web-diagrammer) Sekvensgrafer er en graftype i TI-Nspire CAS, der bruges til at illustrere talfølger, der er defineret rekursivt, løse differensligninger (herunder koblede differensligninger), illustrere iteration mm. indenfor rammerne af en applikation i TI-Nspire CAS. De følgende fire eksempler viser hvordan denne graftype anvendes i typiske problemstillinger, der omhandler sådanne rekursive talfølger. Graftypen er defineret i grafværkstedet.
2 Eksempel 1: Hunden og haren Vi tager udgangspunkt i et klassisk problem: En hund befinder sig på kanten af en græsmark, der er 150 meter bred, da den opdager en hare på den modsatte kant af græsmarken. Hunden sætter straks efter haren. Hunden springer 9 meter for hver gang haren springer 7 meter. Hvor langt skal hunden løbe før den har indhentet haren? Vi åbner nu for applikationen Grafer og skifter til sekvensgrafer. Det sker nemmest ved at højreklikke på forskriften i indtastningslinjen. Bemærkning: Graftypen kaldes Liste fra formel, hvilket ikke er helt smart. Vi skifter da til sekvens-mode, hvor de rekursive funktioner som udgangspunkt kaldes u1, u2, : 1
3 Som udgangspunkt kan vi selvfølgelig bare beholde navnene, men det er ofte mere overskueligt at skifte navne til noget mere sigende! Så vi omdøber u1 til hund og indskriver den rekursive forskrift: hund(n) = hund(n-1)+9 (idet hunden løber 9 meter i hvert spring) Startled: 0 (idet vi regner ud fra hundens startposition på kanten af græsmarken) 0 n 99 nstep = 1 (hvor vi har skiftet startværdien for n til 0) Hvis vi udfører en zoom-fit (fx ved at højreklikke i grafrummet) får vi nu et passende skærmbillede, der viser hvordan hunden løber: Lad os med det samme tilføje haren: hare(n)=hare(n-1)+7 (idet haren løber 7 meter i hvert spring) Startled: 150 (idet haren har et forspring på 150 meter, da den bliver opdaget) 0 n 99 nstep = 1 (hvor vi igen husker at skifte startværdien for n til 0!) Herefter får vi en grafisk fremstilling af begge dyrs positioner som funktion af antallet af spring. 2
4 Af grafen fremgår da tydeligt at hunden indhenter haren indenfor grafrummet, hvor de to grafer skærer hinanden. Vi kan fx finde skæringspunktet ved at spore en sekvensgraf (højreklik på grafen for at få lov til at spore) eller ved at kigge i den tilhørende tabel, der fås frem ved at taste CTRL + T: 3
5 Vi ser da at hunden indhenter haren efter 75 spring, og at hunden på dette tidspunkt har løbet 675 meter (vi springer op og ned mellem de to grafer med piletasterne for at bekræfte, at der er tale om det samme grafpunkt). Koordinaterne til skæringspunktet fastfryses ved at taste Enter i sporingen. Tabellen bekræfter det samme! På det tidspunkt kan vi nu lege videre med graferne på forskellig vis. Fx kan vi kigge på afstanden mellem de to dyr ved at trække deres positioner fra hinanden. Vær opmærksom på startleddet, som vi selv må regne ud! forspring(n)=hare(n)-hund(n) Startled: n 99 nstep = 1 Grafen for forspring skjuler vi bare! Af tabellen fremgår da tydeligt, at forspringet formindskes med 2 for hvert spring (i overensstemmelse med at hunden springer 9 meter, mens haren kun springer 7 meter). Da 2 gå 75 gange op i 150 meter (den oprindelige forskel) følger da netop at hunden indhenter haren efter 75 spring. Det giver ikke umiddelbar hvor langt hunden har løbet, men der kan vi jo bare gange hundens spring på 9 meter med antallet af spring, dvs
6 Bemærkning: Tabellen opdateres ikke automatisk med den nye talfølge. Det er nemmest at taste CRTL T to gage for at slukke og tænde for tabellen. Men det er også oplagt at graferne er lineære. Det passer fint med at en lineær vækst er en plus-vækst, dvs. vi lægge det samme antal meter til for hvert spring. Ydermere må springets længde netop angive hældningskoefficienten! Det er altså oplagt at forskrifterne for hundens og harens løb er givet ved hund(n) = 9 n hare(n) = 7 n+150 Afsætter vi en ret linje oven i grafen og beder vi om at få oplyst dens ligning bekræftes vi netop i disse ligninger: Vi kunne ad også finde skæringspunktet direkte mellem de to linjer ved hjælp af menupunktet Geometri Punkter og Linjer Skæringspunkter. Når først vi har de eksplicitte forskrifter til rådighed kan vi selvfølgelig løse problemet rent symbolsk. Vi kan også opstille 3 ligninger med tre ubekendte og løse dem men det kræver en vis matematisk modenhed! 5
7 Læg mærke til, at vi ikke har koblet differensligningerne i det foregående. Hundens nye position afhænger kun af dens egen foregående position! Læg også mærke til, at differensligningerne (de rekursive forskrifter) er af første orden, dvs. hver ny position skridt afhænger kun af det foregående skridt. I det næste eksempel skal vi se nærmere på en anden ordens differensligning, hvor forskriften afhænger af de to foregående skridt, hvorfor der skal være to startled. Læg endeligt mærke til, at vi har været omhyggelige med at specificere det samme startpunkt (n = 0) for de tre sekvensfunktioner hund, hare og forspring. I modsat fald ville der gå kludder i beregningen af fx forspringfunktionen! 6
8 Eksempel 2: Fibonaccitallene Det næste eksempel er en klassiker. Som bekendt er fibonaccitallene defineret som talfølgen: 1, 1, 2, 3, 5, 8, 13,, hvor hvert nyt fibonaccital er summen af de to foregående! Fibonaccitallene er defineret ud fra den rekursive forskrift Fib(n)=Fib(n-1)+Fib(n-2) Startled: 1,1 1 n 99 nstep = 1 Læg mærke til at startværdien for indekset n denne gang er 1! Vi åbner derfor for applikationen Grafer og skifter til graftype Liste fra formel og indskriver/tegner grafen for sekvensfunktionen: Grafen ser umiddelbart meget flad ud undtagen på det sidste stykke, hvor den vokser drastisk (læg mærke til at y-aksen slutter ved ). Det kunne tyde på en eksponentiel vækst, som jo netop vokser eksplosivt. Vi kan ikke umiddelbart udføre en eksponentiel regression, da vi ikke har overført sekvensen til lister og regneark. Det er ikke fordi det er så svært, men inden da kan vi lige tjekke grafisk om ideen om eksponentiel vækst holder vand. Vi opretter da en ny logaritmisk graf baseret på forskriften log_fib(n)=log(fib(n)) Startled: 0 1 n 99 nstep = 1 7
9 Hvis der er tale om en eksponentiel vækst skal den logaritmisk transformerede graf være lineær: Det ser lovende ud, og vi kunne nu godt få en ligning frem vi kunne lege videre med. Men inden da vil vi lige vise hvordan man overføre en sekvensfunktion til lister og regneark, da det kan være nyttigt i andre sammenhænge. Forskriften for en sekvensfunktion er desværre ikke listerobust, så både n- og fib(n)- værdierne opbygges ved hjælp af seq-kommandoen: Den eksponentielle regression er ikke helt perfekt, men heller ikke dårlig. Det er altså noget, der ligner en eksponentiel vækst. Nu er en eksponentiel vækst det samme som en gangevækst og vi tjekker derfor fremskrivningsfaktoren 8
10 fib(n+1)/fib(n) som ville være konstant, hvis der virkeligt var tale om en eksponentiel vækst: vækstfaktor(n)=fib(n+1)/fib(n) startled: 1 1 n 99 nstep = 1 Vi skjuler grafen for vækstfaktoren og overfører i stedet data til en funktionstabel med CTRL-T kommandoen: Til at begynde med svinger fremskrivningsfaktoren lidt op og ned, men meget hurtigt stabiliserer den sig på en fast værdi, der med 14 cifre er givet ved Fibonaccitallene vokser altså asymptotisk som en eksponentiel vækst med den ovenstående fremskrivningsfaktor. Det interessante er nu, at denne værdi kan man med lidt held genkende som det gyldne snit. Det gyldne snit er ikke indbygget som naturkonstant i TI-Nspire, men som vist kan vi nemt selv definere den. Men så kan vi jo finde den asymptotiske startværdi for den eksponentielle vækst ved at tilbageskrive fibonaccitallene: startværdi(n)=fib(n)/ n startled: 1/ 1 n 99 nstep = 1 9
11 Denne gang stabiliserer startværdien sig også relativt hurtigt, men derefter flakser den lidt på de allersidste cifre, hvilket skyldes numeriske afrundingsfejl. Tallet er sværere at genkende, men hvis vi kigger på kvadratet for tallet går det (udregningen af startværdi-funktionen bliver meget hurtigt numerisk ustabil, så vi overfører bare tallene fra tabellen direkte): Det ser altså ud som om der gælder: startværdi = 1 5 Fibonaccitallene vokser altså asymptotisk som den eksponentielle vækst fib() n = 5 2 Men vi kan også se på restleddet (residualet). Da det typisk fremkommer som differens mellem to meget store tal er værdien vi finder hurtigt meget upræcis, så vi kan ikke forvente den samme fine overensstemmelse! n 10
12 n residual(n)=fib(n) startled: 1 2 (startværdien er faktisk overflødig!) 10 1 n 20 nstep = 1 (Læg mærke til at vi denne gang kun kigger på de første 20 led) Igen kigger vi på grafen (i et nyt grafrum!) og vurderer om der kan være tale om en eksponentiel vækst (du slår forbind med linjer til ved at højreklikke på grafen og vælge attributter!): Denne gang skifter vi fortegn hver gang, så det er ikke en klassisk eksponentiel vækst, men ellers kunne den godt ligne. Vi kigger derfor igen på fremskrivningsfaktoren: 11
13 fakt_res(n)=residual(n+1)/residual(n) startled: 1 5 (startværdien er faktisk overflødig) 2 1 n 20 nstep = 1 De første seks cifre er konstante, mens resten blafrer, hvilket vi tolker som numerisk ustabilitet, fordi vi trækker to store tal fra hinanden. Ydermere kan vi nemt genkende fremskrivningsfaktoren, som igen er tæt knyttet til det gyldne snit! Vi vover pelsen og kigger nu på den tilsvarende startværdi for den utraditionelle eksponentielle vækst: start_res(n)=residual(n)/(1- ) n startled: 1 n 20 nstep = 1 Og med 6 decimaler ser det ud til at den er konstant. Ydermere kender vi jo så konstanten, der bortset fra fortegnet er den samme som før! 12
14 Dermed har vi gætte den samlede formel for fibonaccitallene: fibonacci n = Formlen, der kaldes Binets formel, er meget berømt og du kan godt få din matematiklærer til at udlede den ud fra differensligningen på mere systematisk vis, men så begynder det at ligne et studieretningsprojekt Her tjekker vi dels numerisk, dels symbolsk, at formlen fungerer. Læg mærke til at formlen først fungerer alment, når vi skifter til komplekst rektangulært format, fordi vi opløfter et negativt tal til en potens (det gøres under indstillinger)! Til gengæld rummer formlen så lige pludselig cosinus og sinus. Hvis vi vil udvide fibonaccitallene til vilkårlige værdier af n, fås altså komplekse værdier! n n 13
15 Tegner vi grafen for realdelen kan vi se, hvordan den netop går gennem alle fibonaccitallene: Men rekursionsformlen virker altså kun overalt, hvis vi også inddrager imaginærdelen. 14
16 Eksempel 3: Radioaktive henfaldskæder Igen tager vi udgangspunkt i et konkret problem: 210 Bi og 210 Po er to nuklider i den såkaldte uranfamilie (henfaldskæde) af stoffer, som dannes gennem radioaktivt henfald af 238U og dens døtre. I henfaldskæden henfalder 210 Bi til 210 Po med halveringstiden 5,013d, mens 210 Po henfalder med halveringstid 138,4d til det stabile nuklid 206 Pb. Opstil en model, der beskriver dette henfald og brug det til at tå tegnet en graf over antallet af moder- og datterkerner som funktion af tiden gennem fx 250 d. Vi antager nu at der er givet et vist antal kerner, fx 1000 af det første nuklid Bi-210, der henfalder med halveringstiden 5,013d. Dette henfald er eksponentielt med en fremskrivningsfaktor a Bi og en henfaldskonstant k Bi, der udregnes således Vi kan derfor nemt opstille henfaldsligningen for Bi-210: Bi_210(n):=Bi_210(n-1)-k_Bi*Bi_210(n-1) Startled: n 250 nstep=1 15
17 Når vi derefter vender os mod Po-210 bliver det lidt mere indviklet. Po-210 har halveringstiden 138,4d og dermed en fremskrivningsfaktor a Po og en henfaldskonstant k Po, der derfor er givet ved Til at begynde med er der ingen Po-kerner, men så dannes der Po-kerner som følge af Bi-henfaldene, ligesom der forsvinder Po-kerner på grund af henfaldet til nuklidet Pb-206: Po_210(n):=Po_210(n-1)+k_Bi*Bi_210(n-1)-k_Po*Po_210(n-1) Startled: 0 0 n 250 nstep=1 Vi ser da at antallet af Po-kerner til at begynde med vokser kraftigt for derefter at dø langsomt ud. Vi kan som vist benytte sporingsmekanismen til at finde det maksimale antal Po-kerner: Efter 25 dage topper antallet af Po-kerner med 885 kerner (ud af de 1000 mulige). Endelig kan vi se på antallet af stabile Pb-kerner, der opstår som følge af henfaldet af Po-kerner: Pb_206(n):=Pb_206(n-1) + k_po Po_210(n-1) Startled: 0 0 n 250 nstep=1 16
18 Læg mærke til at der er indbygget en balance i ligningerne: De kerner, der forsvinder fra Bi-210 dukker op som Po-210-kerner og tilsvarende for de kerner, der forsvinder fra Po-210, der dukker op som antallet af Pb-kerner. Det samlede antal er derfor bevaret: 17
19 Hvordan ligger det nu med en eventuel eksponentiel vækst? Som i det foregående eksempel kan vi oprette en ny graf med logaritmerne til de tre antal kerner: Ikke overraskende henfalder antallet af Bi-kerner eksponentielt. Men det ser også ud til at antallet af Po-kerner henfalder asymptotisk eksponentielt. Vi har lagt en ret linje ind over grafen, så man tydeligere kan se den asymptotiske sammenhæng! Det kan vi forstå således: Når antallet af Bi-kerner dør ud kommer der ikke længere en tilvækst fra de henfaldne Bi-kerner, hvorfor antallet af de tiloversblevne Po-kerner begynder at henfalde eksponentielt. Vi kan tjekke de fundne påstande ved at udregne de tilhørende fremskrivningsfaktorer: Factor_bi(n):=Bi_210(n+1)/ Bi_210(n) Startled: 0 n 250 nstep=1 Factor_po(n):=Po_210(n+1)/Po_210(n) Startled: 0 n 250 nstep=1 (hvor vi ikke behøver oplyse startleddene) 18
20 Som forventet er fremskrivningsfaktoren for Bi-210 konstant og svarer netop til værdien af a_bi: Derimod ændrer fremskrivningsfaktoren for Po sig stille og roligt indtil den får stabiliseret sig på værdien af a_po: Dermed har vi fastslået de vigtigste træk ved henfaldskædens opførsel. 19
21 Hvis man er fortrolig med differensligninger kan man godt løse dem eksakt. Vi har allerede fundet udtrykket for Bi-210: Bi_210(x)= 1000 a_bi x = x Et grafisk check ser rimelig overbevisende ud! Udtrykket for Po ser mere indviklet ud! Men vi ved at den asymptotisk henfalder eksponentielt. Vi kan så også finde den asymptotiske startværdi og gemme den som b_po: start(n):=po_210(n)/ a_po n Startled: 0 n 250 nstep=1 Derefter er vejen åben for at se på resten, dvs. forskellen på Po_210 og den asymptotiske eksponentielle vækst (ligesom ved fibonaccitallene): dif(n):=b_po a_po n - Po_210(n) Startled: b_po 0 n 250 nstep=1 20
22 Det ser lovende ud! Det ligner faktisk temmelig meget det eksponentielle henfald af Bi Ser vi på fremskrivningsfaktoren finder vi da også netop den samme fremskrivningsfaktor. Tilbage er så blot at finde startværdien for forskellen (som vi strengt taget godt kan se direkte af formlen må være b_po!). Deraf følger at antallet af Po-210 kerner har forskriften Po(n)=b_Po (a_po n -a_bi n ) Et grafisk check understøtter denne formel! Det er bemærkelsesværdigt i hvor høj grad opførslen af Po-kerner ligner opførslen af Fibonaccitallene! 21
23 Tilbage er så kun antallet af Pb-kerner. Men her kan vi blot benytte, at summen af de tre antal kerner er bevaret, dvs. konstant = 1000, hvorfor forskriften er givet ved: Pb(n)= a_bi n +b_po a_bi n -b_po a_po n 22
24 Eksempel 4: Feigenbaum iteration og kaos Som det sidste eksempel på anvendelse af sekvensgrafer ser vi på et klassisk eksempel på kaotisk opførsel: Feigenbaumiterationen ( ) x = 1 4a + x 1 x n n n med en startværdi x0, der ligger mellem 0 og 1 og en parameter a, der ligeledes ligger mellem 0 og 1. Vi kan tegne grafen for iterationen ved at indskrive den som en sekvensgraf: feig(n)=4 a feig(n-1) (1-feig(n-1)) startled: n 250 nstep = 1 Læg mærke til at vi har indført en skyder for at kunne styre parameteren a. Skyderen gennemløber intervallet fra 0 til 1 i spring af Man kan animere parameteren a og se hvordan iterationen opfører sig: Først gennemløber man alle periodefordoblingerne: Grafen ligner nærmest en lynlås, der bliver lynet op, derefter to lynlåse, der bliver lynet op, dernæst fire lynlåse, der bliver lynet op osv. derefter skifter man mellem kaotiske områder og vinduer, hvor der igen er en tydelig periode som her vist med en tre-cykel svarende til a = osv. Det er dynamikken der er afgørende her for ens oplevelse af iterationen og den kan vi desværre ikke vise på et stykke papir! Vi viser dog også et eksempel på iterationens forløb i et kaotisk område: 23
25 Udover den sædvanlige tidsseriegraf, eller (n,feig(n))-graf, kan man også få illustreret et web-plot, eller (feig(n),feig(n+1))-graf, ved at vælge attributer, pile ned uret og skifte til webplot (spindelvæv): Tidsserie-graf Webplot Man er da også nødt til at omjustere vinduesgrænserne. I første omgang kan det klares med en zoom-fit. Men ønsker man et pænt kvadratisk zoom må man efterfølgende ind og pille ved vinduesgræserne: VI skal da sætte xmax passende op så der bliver plads til et enhedskvadrat. Her vælger vi vinduesgrænserne og efterjusterer med Zoom-kvadrat: -0.1 < x <
26 Forbinder vi linjestykkerne fås nu det klassiske webplot: Igen er dynamikken afgørende for ens oplevelse af iterationens opførsel. Vi viser igen trecyklen med parameterværdien Som vist kan man også spore 25
27 web-plottet og dermed også på den måde få en fornemmelse for iterationens forløb: Dermed har vi udtømt de muligheder der umiddelbart ligger i sekvensgraferne. Men selvfølgelig kan man også undersøge feigenbaum-iterationen ved hjælp af andre repræsentationer. Et egentligt figentræ med parameteren a ud af førsteaksen og de asymptotiske iterationer op af anden-aksen er svær at tegne. Men man kan tegne skyggerne af figentræet ved at sammensætte iterationsfunktionen med sig selv et passende antal gange og så afbilde den første itererede af 1/2, den anden itererede af 1/2 osv. som funktion af parameteren a: Det giver en ganske god fornemmelse for sammenhængen mellem de forskellige repræsentationer. Vi kan selvfølgelig også regne på iterationerne. Men pas på med at presse maskinen for hårdt det er rimeligt heftige udtryk! Man kan selvfølgelig også kopiere et baggrundsbillede af figentræet i en passende opløsning ind i fx et grafrum og så efterfølgende justere vinduesgrænser og skyderen, så de passer sammen med figentræet. Her er det vist med parameteren k = 4a sammen med et passende billede fra wikipedia: 26
28 Regner vi videre kan vi nu finde forskellige interessante parameterværdier: Her finder vi fx alle superstabile cykler med orden op til 5, idet vi efterfølgende blokerer for det allerede fundne fikspunkt og tilsvarende for den allerede funnde to-cykel: 27
29 Der er altså netop 2 firecykler og tre 5-cykler, som man efterfølgende kan gå ind og kigge på i detaljer! De er ikke alle lige nemme at finde! 28
30 De fire første var nemme at finde, men når vi prøver med den sidste 5-cykel går det galt: Det skyldes numerisk ustabilitet, som netop er altafgørende i kaos. Den almindelige solve-rutine finder kun løsningen med begrænset nøjagtighed (ca. 6 cifre) og derfor slipper vi ret hurtigt 5-cyklen og ryger i stedet ud i et kaotisk forløb, sådan som det tydeligt fremgår af tidsserien til højre. I stedet skal vi finde den præcise løsning ved at dirigere solve-kommandoen med en startværdi, som her kan sættes til 1, da den sidste cykelværdi har en parameterværdi meget tæt på 1: Indsætter vi nu i stedet den præcise værdi så går det fint: Vi slutter eksemplet med Feigenbaumiteration med en bemærkning om startleddet. Når man opretter en sekvensgraf er det ikke noget problem at indføre parametre i selve sekvensgrafens forskrift. Derimod kan man ikke uden videre indføre parametre i startleddet. Man kan godt nok indskrive et udtryk i startleddet, men det udregnes med de aktuelle værdier og derfor afhænger startleddet ikke dynamisk af eventuelle parametre. I Feigenbaumiterationen ville det ellers være rart at kunne lade iterationen afhænge af såvel startværdien x 0 som 29
31 feigenbaumparameteren a. Det kan man nu opnå ved hjælp af et lille trick. I stedet for at indskrive forskriften på formen feig(n)=4 a feig(n-1) (1-feig(n-1)), så udvider vi definitionen til en egentlig rekursiv definition: ( ) 4 a feig( n 1) 1 feig( n 1), n> 1 feig() n = x0, n= 1 Derved sikrer vi os at iterationen starter med værdien af x 0. Til gengæld kan vi så ikke længere bruge startleddet til noget, så det sætter vi bare til undef: ( ) 4 a feig( n 1) 1 feig( n 1), n> 1 feig() n = x0, n= 1 startled: undef 0 n 250 nstep = 1 Læg mærke til at n løber fra 0 til 250, men at n=0 ikke bruges til noget, idet den egentlige startværdi nu ligger i 1 og den styres af forskriften. Nu kan vi lege med to skydere: En lodret skyder for startværdien x 0 og en vandret skyder for feigenbaumparameteren a. Derved kan vi fx vise eksperimentelt, at opførslen af iterationen ikke afhænger nævneværdigt af valget af startværdi: Her er det illustreret i området med en trecykel, hvor iterationen svinger ind på trecyklen uafhængigt af startværdien, men i almindelighed går det hurtigere når x 0 er tæt på 0.5! 30
Differentialligninger med TI Nspire CAS version 3.1
 Differentialligninger med TI Nspire CAS version 3.1 Der er tilføjet en ny graftype til Graf værkstedet kaldet Diff lign. Denne nye graftype er en implementering af differentialligningerne som vi kender
Differentialligninger med TI Nspire CAS version 3.1 Der er tilføjet en ny graftype til Graf værkstedet kaldet Diff lign. Denne nye graftype er en implementering af differentialligningerne som vi kender
Hvad er nyt i version 3.6?
 Hvad er nyt i version 3.6? 1. Dokumentformater Den afgørende nyhed og også den mest problematiske er indførelsen af nye dokumentformater: Vi har hidtil arbejdet med et flydende dokumentformat. Når man
Hvad er nyt i version 3.6? 1. Dokumentformater Den afgørende nyhed og også den mest problematiske er indførelsen af nye dokumentformater: Vi har hidtil arbejdet med et flydende dokumentformat. Når man
Logaritmiske koordinatsystemer med TI-Nspire CAS version 3.6
 Logaritmiske koordinatsystemer med TI-Nspire CAS version 3.6 Indholdsfortegnelse: Enkelt logaritmisk koordinatsystem side 1 Eksempel på brug af enkelt logaritmisk koordinatsystem ud fra tabel side 2 Dobbelt
Logaritmiske koordinatsystemer med TI-Nspire CAS version 3.6 Indholdsfortegnelse: Enkelt logaritmisk koordinatsystem side 1 Eksempel på brug af enkelt logaritmisk koordinatsystem ud fra tabel side 2 Dobbelt
Eksempel på logistisk vækst med TI-Nspire CAS
 Eksempel på logistisk vækst med TI-Nspire CAS Tabellen herunder viser udviklingen af USA's befolkning fra 1850-1910 hvor befolkningstallet er angivet i millioner: Vi har tidligere redegjort for at antallet
Eksempel på logistisk vækst med TI-Nspire CAS Tabellen herunder viser udviklingen af USA's befolkning fra 1850-1910 hvor befolkningstallet er angivet i millioner: Vi har tidligere redegjort for at antallet
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Projekt 6.1 Rygtespredning - modellering af logistisk vækst
 Projekt 6.1 Rygtespredning - modellering af logistisk vækst (Projektet anvender værktøjsprogrammet TI Nspire) Alle de tilstedeværende i klassen tildeles et nummer, så med 28 elever i klassen uddeles numrene
Projekt 6.1 Rygtespredning - modellering af logistisk vækst (Projektet anvender værktøjsprogrammet TI Nspire) Alle de tilstedeværende i klassen tildeles et nummer, så med 28 elever i klassen uddeles numrene
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT.
 Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT. Projektet kan bl.a. anvendes til et forløb, hvor en af målsætningerne er at lære om samspillet mellem værktøjsprogrammernes geometriske
Projekt 1.4 Tagrendeproblemet en instruktiv øvelse i modellering med IT. Projektet kan bl.a. anvendes til et forløb, hvor en af målsætningerne er at lære om samspillet mellem værktøjsprogrammernes geometriske
Graph brugermanual til matematik C
 Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Kapitel 7 Matematiske vækstmodeller
 Matematiske vækstmodeller I matematik undersøger man ofte variables afhængighed af hinanden. Her ser man, at samme type af sammenhænge tit forekommer inden for en lang række forskellige områder. I kapitel
Matematiske vækstmodeller I matematik undersøger man ofte variables afhængighed af hinanden. Her ser man, at samme type af sammenhænge tit forekommer inden for en lang række forskellige områder. I kapitel
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
Kapitel 3 Lineære sammenhænge
 Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Matematik C (må anvendes på Ørestad Gymnasium) Lineære sammenhænge Det sker tit, at man har flere variable, der beskriver en situation, og at der en sammenhæng mellem de variable. Enhver formel er faktisk
Excel tutorial om lineær regression
 Excel tutorial om lineær regression I denne tutorial skal du lære at foretage lineær regression i Microsoft Excel 2007. Det forudsættes, at læseren har været igennem det indledende om lineære funktioner.
Excel tutorial om lineær regression I denne tutorial skal du lære at foretage lineær regression i Microsoft Excel 2007. Det forudsættes, at læseren har været igennem det indledende om lineære funktioner.
Lineære sammenhænge, residualplot og regression
 Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Matematik A og Informationsteknologi B
 Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Matematik A og Informationsteknologi B Projektopgave 2 Eksponentielle modeller Benjamin Andreas Olander Christiansen Jens Werner Nielsen Klasse 2.4 6. december 2010 Vejledere: Jørn Christian Bendtsen og
Afstandsformlen og Cirklens Ligning
 Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
Afstandsformlen og Cirklens Ligning Frank Villa 19. august 2012 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk.
Rygtespredning: Et logistisk eksperiment
 Rygtespredning: Et logistisk eksperiment For at det nu ikke skal ende i en omgang teoretisk tørsvømning er det vist på tide vi kigger på et konkret logistisk eksperiment. Der er selvfølgelig flere muligheder,
Rygtespredning: Et logistisk eksperiment For at det nu ikke skal ende i en omgang teoretisk tørsvømning er det vist på tide vi kigger på et konkret logistisk eksperiment. Der er selvfølgelig flere muligheder,
Eksponentiel regression med TI-Nspire ved transformation af data
 Eksponentiel regression med TI-Nspire ved transformation af data En vigtig metode til at få overblik over data er at tranformere dem, således at der fremkommer en lineær sammenhæng. Ordet transformation
Eksponentiel regression med TI-Nspire ved transformation af data En vigtig metode til at få overblik over data er at tranformere dem, således at der fremkommer en lineær sammenhæng. Ordet transformation
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Nspire 4.2 kom godt i gang
 Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Skriv punkternes koordinater i regnearket, og brug værktøjet To variabel regressionsanalyse.
 Opdateret 28. maj 2014. MD Ofte brugte kommandoer i Geogebra. Generelle Punktet navngives A Geogebra navngiver punktet Funktionen navngives f Funktionen navngives af Geogebra Punktet på grafen for f med
Opdateret 28. maj 2014. MD Ofte brugte kommandoer i Geogebra. Generelle Punktet navngives A Geogebra navngiver punktet Funktionen navngives f Funktionen navngives af Geogebra Punktet på grafen for f med
Funktioner. 3. del Karsten Juul
 Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Maple. Skærmbilledet. Vi starter med at se lidt nærmere på opstartsbilledet i Maple. Værktøjslinje til indtastningsområdet. Menulinje.
 Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Maple Dette kapitel giver en kort introduktion til hvordan Maple 12 kan benyttes til at løse mange af de opgaver, som man bliver mødt med i matematiktimerne på HHX. Skærmbilledet Vi starter med at se lidt
Projekt 1.3 Brydningsloven
 Projekt 1.3 Brydningsloven Når en bølge, fx en lysbølge, rammer en grænseflade mellem to stoffer, vil bølgen normalt blive spaltet i to: Noget af bølgen kastes tilbage (spejling), hvor udfaldsvinklen u
Projekt 1.3 Brydningsloven Når en bølge, fx en lysbølge, rammer en grænseflade mellem to stoffer, vil bølgen normalt blive spaltet i to: Noget af bølgen kastes tilbage (spejling), hvor udfaldsvinklen u
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Algebra - Teori og problemløsning
 Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Algebra - Teori og problemløsning, januar 05, Kirsten Rosenkilde. Algebra - Teori og problemløsning Kapitel -3 giver en grundlæggende introduktion til at omskrive udtryk, faktorisere og løse ligningssystemer.
Eksponentielle sammenhænge
 Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Eksponentielle sammenhænge 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Indholdsfortegnelse Variabel-sammenhænge... 1 1. Hvad er en eksponentiel sammenhæng?... 2 2. Forklaring med ord af eksponentiel vækst... 2, 6
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
For at få tegnet en graf trykkes på knappen for graftegning. Knap for graftegning
 Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Om at finde bedste rette linie med Excel
 Om at finde bedste rette linie med Excel Det er en vigtig og interessant opgave at beskrive fænomener i naturen eller i samfundet matematisk. Dels for at få en forståelse af sammenhængende indenfor det
Om at finde bedste rette linie med Excel Det er en vigtig og interessant opgave at beskrive fænomener i naturen eller i samfundet matematisk. Dels for at få en forståelse af sammenhængende indenfor det
Some like it HOT: Højere Ordens Tænkning med CAS
 Some like it HOT: Højere Ordens Tænkning med CAS Bjørn Felsager, Haslev Gymnasium & HF, 2001 I år er det første år, hvor CAS-forsøget er et standardforsøg og alle studentereksamensopgaverne derfor foreligger
Some like it HOT: Højere Ordens Tænkning med CAS Bjørn Felsager, Haslev Gymnasium & HF, 2001 I år er det første år, hvor CAS-forsøget er et standardforsøg og alle studentereksamensopgaverne derfor foreligger
Gratisprogrammet 27. september 2011
 Gratisprogrammet 27. september 2011 1 Brugerfladen: Små indledende øvelser: OBS: Hvis et eller andet ikke fungerer, som du forventer, skal du nok vælge en anden tilstand. Dette ses til højre for ikonerne
Gratisprogrammet 27. september 2011 1 Brugerfladen: Små indledende øvelser: OBS: Hvis et eller andet ikke fungerer, som du forventer, skal du nok vælge en anden tilstand. Dette ses til højre for ikonerne
Eksamensspørgsmål: Eksponentiel vækst
 Eksamensspørgsmål: Eksponentiel vækst Indhold Definition:... Eksempel :... Begndelsesværdien b... Fremskrivningsfaktoren a... Eksempel :... Formlerne for a og b... 3 Eksempel 3:... 3 Bevis for formlen
Eksamensspørgsmål: Eksponentiel vækst Indhold Definition:... Eksempel :... Begndelsesværdien b... Fremskrivningsfaktoren a... Eksempel :... Formlerne for a og b... 3 Eksempel 3:... 3 Bevis for formlen
Projekt 2.5 Brændpunkt og ledelinje
 Projekter. Kapitel. Projekt.5 Brændpunkt og ledelinje Projekt.5 Brændpunkt og ledelinje En af de vigtigste egenskaber ved en parabel er dens brændpunkt og en af parablens vigtigste anvendelser er som profilen
Projekter. Kapitel. Projekt.5 Brændpunkt og ledelinje Projekt.5 Brændpunkt og ledelinje En af de vigtigste egenskaber ved en parabel er dens brændpunkt og en af parablens vigtigste anvendelser er som profilen
Arealet af en trekant Der er mange formler for arealet af en trekant. Den mest kendte er selvfølgelig
 Arealet af en trekant Der er mange formler for arealet af en trekant. Den mest kendte er selvfølgelig som også findes i en trigonometrisk variant, den såkaldte 'appelsin'-formel: Men da en trekants form
Arealet af en trekant Der er mange formler for arealet af en trekant. Den mest kendte er selvfølgelig som også findes i en trigonometrisk variant, den såkaldte 'appelsin'-formel: Men da en trekants form
Parameterkurver. Et eksempel på en rapport
 x Parameterkurver Et eksempel på en rapport Parameterkurver 0x MA side af 7 Hypocykloiden A B Idet vi anvender startværdierne for A og B som angivet, er en generel parameterfremstilling for hypocykloiden
x Parameterkurver Et eksempel på en rapport Parameterkurver 0x MA side af 7 Hypocykloiden A B Idet vi anvender startværdierne for A og B som angivet, er en generel parameterfremstilling for hypocykloiden
Projekt 2.5 Brændpunkt og ledelinje for parabler
 Hvad er matematik? Projekter: Kapitel. Projekt.5 Brændpunkt og ledelinje for parabler Projekt.5 Brændpunkt og ledelinje for parabler En af de vigtigste egenskaber ved en parabel er, at den har et såkaldt
Hvad er matematik? Projekter: Kapitel. Projekt.5 Brændpunkt og ledelinje for parabler Projekt.5 Brændpunkt og ledelinje for parabler En af de vigtigste egenskaber ved en parabel er, at den har et såkaldt
Grafværktøjer til GeoMeter Grafværktøjer Hjælp Grafværktøjer.gsp Grafværktøjer
 Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Projekt 2.1: Parabolantenner og parabelsyning
 Projekter: Kapitel Projekt.1: Parabolantenner og parabelsyning En af de vigtigste egenskaber ved en parabel er dens brændpunkt og en af parablens vigtigste anvendelser er som profilen for en parabolantenne,
Projekter: Kapitel Projekt.1: Parabolantenner og parabelsyning En af de vigtigste egenskaber ved en parabel er dens brændpunkt og en af parablens vigtigste anvendelser er som profilen for en parabolantenne,
Deskriptiv statistik (grupperede observationer)
 Deskriptiv statistik (grupperede observationer) Tallene er hentet fra Arbejdsbog B1 (2.udg.) eller Arbejdsbog B2, øvelse 408: Der åbnes et Lister og Regneark værksted og observationerne indtastes og navngives:
Deskriptiv statistik (grupperede observationer) Tallene er hentet fra Arbejdsbog B1 (2.udg.) eller Arbejdsbog B2, øvelse 408: Der åbnes et Lister og Regneark værksted og observationerne indtastes og navngives:
2 Erik Vestergaard www.matematikfysik.dk
 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra
 QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra Nspire: Vi har et datasæt. Der er overordnet to metoder til at tegne sumkurver i programmet, og vi beskriver
QR15 Vejledning i at bestemme kvartilsæt og at tegne sumkurver med Nspire, Maple og Geogebra Nspire: Vi har et datasæt. Der er overordnet to metoder til at tegne sumkurver i programmet, og vi beskriver
Projekt 8.6 Linearisering af data fra radioaktivt henfald
 Projekt 8.6 Linearisering af data fra radioaktivt henfald Bemærk, at i det følgende er værktøjet TINspire anvendt. Det kan lige så godt laves i et andet værktøj. En vigtig metode til at få overblik over
Projekt 8.6 Linearisering af data fra radioaktivt henfald Bemærk, at i det følgende er værktøjet TINspire anvendt. Det kan lige så godt laves i et andet værktøj. En vigtig metode til at få overblik over
Computerundervisning
 Frederiksberg Seminarium Computerundervisning Koordinatsystemer og Funktioner Lærervejledning 12-02-2009 Udarbejdet af: Pernille Suhr Poulsen Christina Klitlyng Julie Nielsen Indhold Introduktion... 3
Frederiksberg Seminarium Computerundervisning Koordinatsystemer og Funktioner Lærervejledning 12-02-2009 Udarbejdet af: Pernille Suhr Poulsen Christina Klitlyng Julie Nielsen Indhold Introduktion... 3
Matematik A STX 18. maj 2017 Vejledende løsning De første 6 opgaver løses uden hjælpemidler
 ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
ADVARSEL! Før du anvender løsningerne, så husk at læs betingelserne for løsningerne, som du kan finde på hjemmesiden. Indeholder: Matematik A, STX 18 maj Matematik A, STX 23 maj Matematik A, STX 15 august
Andengradsligninger. Frank Nasser. 11. juli 2011
 Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Velkommen til TI-Nspire CAS 2.0 (Lærerversion)
 Velkommen til TI-Nspire CAS 2.0 (Lærerversion) Når du åbner for TI-Nspire CAS i en standardopsætning ser brugerfladen således ud (hvis ikke, så vælg Dialogboks > Indlæs standardområdet): I midterpanelet
Velkommen til TI-Nspire CAS 2.0 (Lærerversion) Når du åbner for TI-Nspire CAS i en standardopsætning ser brugerfladen således ud (hvis ikke, så vælg Dialogboks > Indlæs standardområdet): I midterpanelet
Erik Vestergaard 1. Opgaver. i Lineære. funktioner. og modeller
 Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Funktioner. 2. del Karsten Juul
 Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Matematik A. 5 timers skriftlig prøve. Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA. Undervisningsministeriet
 Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 29. maj 2009 kl. 9.00-14.00 Matematik A 2009 Prøvens varighed er 5 timer.
Højere Teknisk Eksamen i Grønland maj 2009 GLT091-MAA Matematik A 5 timers skriftlig prøve Undervisningsministeriet Fredag den 29. maj 2009 kl. 9.00-14.00 Matematik A 2009 Prøvens varighed er 5 timer.
I tabellen vises en liste med værdier for den uafhængige variabel, og desuden den tilsvarende værdi for den afhængige variabel.
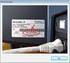 Kapitel 13: Tabeller 13 Resumé af tabeller... 222 Oversigt over trinene i oprettelse af en tabel... 223 Indstilling af tabelparametre... 224 Visning af en automatisk tabel... 226 Oprettelse af en manuel
Kapitel 13: Tabeller 13 Resumé af tabeller... 222 Oversigt over trinene i oprettelse af en tabel... 223 Indstilling af tabelparametre... 224 Visning af en automatisk tabel... 226 Oprettelse af en manuel
Analytisk geometri. Et simpelt eksempel på dette er en ret linje. Som bekendt kan en ret linje skrives på formen
 Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Analtisk geometri Mike Auerbach Odense 2015 Den klassiske geometri beskæftiger sig med alle mulige former for figurer: Linjer, trekanter, cirkler, parabler, ellipser osv. I den analtiske geometri lægger
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009)
 Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
Differentialregning med TI-Interactive! Indledende differentialregning Tangenter Monotoniforhold og ekstremum Optimering Jan Leffers (2009) Indholdsfortegnelse Indholdsfortegnelse...2 Indledende differentialregning...3
12 skarpe! Eksempler på elevaktiverende øvelser med. Indhold
 12 skarpe! Eksempler på elevaktiverende øvelser med Indhold Øvelse Niveau Navn 1 C Elementær geometri 2 C Lineære funktioner 3 C-B Optimering af en æske fra et A4-ark 4 C-B Bestemmelse af forklaringsgrad
12 skarpe! Eksempler på elevaktiverende øvelser med Indhold Øvelse Niveau Navn 1 C Elementær geometri 2 C Lineære funktioner 3 C-B Optimering af en æske fra et A4-ark 4 C-B Bestemmelse af forklaringsgrad
Ting man gør med Vektorfunktioner
 Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Ting man gør med Vektorfunktioner Frank Villa 3. august 13 Dette dokument er en del af MatBog.dk 8-1. IT Teaching Tools. ISBN-13: 978-87-9775--9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Eksponentielle sammenhænge
 Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Eksponentielle sammenhænge Udgave 009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Lineære sammenhænge, udgave 009" Indhold 1 Eksponentielle sammenhænge, ligning og graf 1 Procent 7 3 Hvad fortæller
Introduktion til TI-Nspire 1. Dokumentformat
 1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
Løsninger til eksamensopgaver på A-niveau 2016
 Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Fraktaler Mandelbrots Mængde
 Fraktaler Mandelbrots Mængde Foredragsnoter Af Jonas Lindstrøm Jensen Institut For Matematiske Fag Århus Universitet Indhold Indhold 1 1 Indledning 3 2 Komplekse tal 5 2.1 Definition.......................................
Fraktaler Mandelbrots Mængde Foredragsnoter Af Jonas Lindstrøm Jensen Institut For Matematiske Fag Århus Universitet Indhold Indhold 1 1 Indledning 3 2 Komplekse tal 5 2.1 Definition.......................................
Komplekse tal. Mikkel Stouby Petersen 27. februar 2013
 Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Komplekse tal Mikkel Stouby Petersen 27. februar 2013 1 Motivationen Historien om de komplekse tal er i virkeligheden historien om at fjerne forhindringerne og gøre det umulige muligt. For at se det, vil
Projekt 3.4 Fjerdegradspolynomiets symmetri
 Hvad er matematik? Projekt 3. Fjerdegradspolynomiets symmetri Indledning: Symmetri for polynomier I kapitel har vi set at grafen for et andengradspolynomium p ( x) = a x + x + c altid er symmetrisk omkring
Hvad er matematik? Projekt 3. Fjerdegradspolynomiets symmetri Indledning: Symmetri for polynomier I kapitel har vi set at grafen for et andengradspolynomium p ( x) = a x + x + c altid er symmetrisk omkring
REDIGERING AF REGNEARK
 REDIGERING AF REGNEARK De to første artikler af dette lille "grundkursus" i Excel, nemlig "How to do it" 8 og 9 har været forholdsvis versionsuafhængige, idet de har handlet om ting, som er helt ens i
REDIGERING AF REGNEARK De to første artikler af dette lille "grundkursus" i Excel, nemlig "How to do it" 8 og 9 har været forholdsvis versionsuafhængige, idet de har handlet om ting, som er helt ens i
Potensfunktioner samt proportional og omvent proportional. for hf Karsten Juul
 Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Lineær og kvadratisk programmering med TI NSpire CAS version 3.2
 Lineær og kvadratisk programmering med TI NSpire CAS version 3.2 Indhold 1. Lineær programmering i 2 variable: x og y... 1 Eksempel 1: Elementær grafisk løsning i 2d... 1 Eksempel 1: Grafisk løsning i
Lineær og kvadratisk programmering med TI NSpire CAS version 3.2 Indhold 1. Lineær programmering i 2 variable: x og y... 1 Eksempel 1: Elementær grafisk løsning i 2d... 1 Eksempel 1: Grafisk løsning i
Opgave 1 - Lineær Funktioner. Opgave 2 - Funktioner. Opgave 3 - Tredjegradsligning
 Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
Sh*maa03 1508 Matematik B->A, STX Anders Jørgensen, delprøve 1 - Uden hjælpemidler Følgende opgaver er regnet i hånden, hvorefter de er skrevet ind på PC. Opgave 1 - Lineær Funktioner Vi ved, at år 2001
1.semester: IT-færdigheder
 1.semester: IT-færdigheder Opgave 1: Organisere filer i mapper Du er i gang med en vigtig opgave, og du leder efter et helt bestemt dokument. Du leder og leder og leder, men kan ikke finde det imellem
1.semester: IT-færdigheder Opgave 1: Organisere filer i mapper Du er i gang med en vigtig opgave, og du leder efter et helt bestemt dokument. Du leder og leder og leder, men kan ikke finde det imellem
Differential- regning
 Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Projekt 9.5 Racefordomme i USA og Simpsons paradoks (B og A)
 Projekt 9.5 Racefordomme i USA og Simpsons paradoks (B og A) (Data er hentet fra M. Radelet, "Racial characteristics and imposition of death penalty", American Sociological Review, 46 (1981), pp 918-927
Projekt 9.5 Racefordomme i USA og Simpsons paradoks (B og A) (Data er hentet fra M. Radelet, "Racial characteristics and imposition of death penalty", American Sociological Review, 46 (1981), pp 918-927
Mathcad Survival Guide
 Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Mathcad Survival Guide Mathcad er en blanding mellem et tekstbehandlingsprogram (Word), et regneark (Ecel) og en grafisk CAS-lommeregner. Programmet er velegnet til matematikopgaver, fysikrapporter og
Brugervejledning til Graph
 Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Løsninger til matematik B-niveau HF maj 2016 April 2017
 Løsninger til matematik B-niveau HF maj 2016 April 2017 www.matematikhfsvar.page.tl Cristina Sissee Jensen Side 1 af 4 Løsninger til matematik B-niveau HF maj 2016 April 2017 www.matematikhfsvar.page.tl
Løsninger til matematik B-niveau HF maj 2016 April 2017 www.matematikhfsvar.page.tl Cristina Sissee Jensen Side 1 af 4 Løsninger til matematik B-niveau HF maj 2016 April 2017 www.matematikhfsvar.page.tl
Grønland. Matematik A. Højere teknisk eksamen
 Grønland Matematik A Højere teknisk eksamen Onsdag den 12. maj 2010 kl. 9.00-14.00 Matematik A Prøvens varighed er 5 timer. Alle hjælpemidler er tilladt. Ved valgopgaver må kun det anførte antal afleveres
Grønland Matematik A Højere teknisk eksamen Onsdag den 12. maj 2010 kl. 9.00-14.00 Matematik A Prøvens varighed er 5 timer. Alle hjælpemidler er tilladt. Ved valgopgaver må kun det anførte antal afleveres
Projekt 3.7. Pythagoras sætning
 Projekt 3.7. Pythagoras sætning Flere beviser for Pythagoras sætning... Bevis for Pythagoras sætning ved anvendelse af ensvinklede trekanter... Opgave 1: Et kinesisk og et indisk bevis for Pythagoras sætning...
Projekt 3.7. Pythagoras sætning Flere beviser for Pythagoras sætning... Bevis for Pythagoras sætning ved anvendelse af ensvinklede trekanter... Opgave 1: Et kinesisk og et indisk bevis for Pythagoras sætning...
Projekt 4.10. Minamata-katastrofen. En modellering af ligevægt mellem lineær vækst og eksponentiel henfald
 Projekt 4.10. Minamata-katastrofen. En modellering af ligevægt mellem lineær vækst og eksponentiel henfald Der findes mange situationer, hvor en bestemt størrelse ændres som følge af vekselvirkninger med
Projekt 4.10. Minamata-katastrofen. En modellering af ligevægt mellem lineær vækst og eksponentiel henfald Der findes mange situationer, hvor en bestemt størrelse ændres som følge af vekselvirkninger med
Matematik A, STX. Vejledende eksamensopgaver
 Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
Matematik A, STX EKSAMENSOPGAVER Vejledende eksamensopgaver 2015 Løsninger HF A-NIVEAU AF SAEID Af JAFARI Anders J., Mark Af K. & Saeid J. Anders J., Mark K. & Saeid J. Kun delprøver 2 Kun delprøve 2,
VisiRegn: En e-bro mellem regning og algebra
 Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Artikel i Matematik nr. 2 marts 2001 VisiRegn: En e-bro mellem regning og algebra Inge B. Larsen Siden midten af 80 erne har vi i INFA-projektet arbejdet med at udvikle regne(arks)programmer til skolens
Lineære sammenhænge. Udgave 2. 2009 Karsten Juul
 Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
Lineære sammenhænge Udgave 2 y = 0,5x 2,5 2009 Karsten Juul Dette hæfte er en fortsættelse af hæftet "Variabelsammenhænge, 2. udgave 2009". Indhold 1. Lineære sammenhænge, ligning og graf... 1 2. Lineær
En funktion kaldes eksponentiel, hvis den har en regneforskrift, der kan skrives således: f(x) = b a x eller y = b a x, idet a og b er positive tal.
 Eksponentielle funktioner Indhold Definition:... 1 Om a og b... 2 Tegning af graf for en eksponentiel funktion... 3 Enkeltlogaritmisk koordinatsstem... 4 Logaritmisk skala... 5 Fordoblings- og halveringskonstant...
Eksponentielle funktioner Indhold Definition:... 1 Om a og b... 2 Tegning af graf for en eksponentiel funktion... 3 Enkeltlogaritmisk koordinatsstem... 4 Logaritmisk skala... 5 Fordoblings- og halveringskonstant...
Talrækker. Aktivitet Emne Klassetrin Side
 VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
VisiRegn ideer 3 Talrækker Inge B. Larsen ibl@dpu.dk INFA juli 2001 Indhold: Aktivitet Emne Klassetrin Side Vejledning til Talrækker 2-4 Elevaktiviteter til Talrækker 3.1 Talrækker (1) M-Æ 5-9 3.2 Hanoi-spillet
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Projekt 3.1 Fjerdegradspolynomiets symmetri
 Projekt 3.1 Fjerdegradspolynomiets symmetri I kapitel 3 har vi set at grafen for et andengradspolynomiet p x a x x c () altid er symmetrisk omkring den lodrette akse x. a Tilsvarende er grafen for tredjegradspolynomiet
Projekt 3.1 Fjerdegradspolynomiets symmetri I kapitel 3 har vi set at grafen for et andengradspolynomiet p x a x x c () altid er symmetrisk omkring den lodrette akse x. a Tilsvarende er grafen for tredjegradspolynomiet
Tilsvarende har vbi i kapitel 3 set, at grafen for tredjegradspolynomiet
 Projekt 3 Fjerdegradspolynomiets symmetri Indledning: Symmetri for polynomier I kapitel har vi set at grafen for et andengradspolynomiet altid er symmetrisk omkring den lodrette akse x a p x a x x c ()
Projekt 3 Fjerdegradspolynomiets symmetri Indledning: Symmetri for polynomier I kapitel har vi set at grafen for et andengradspolynomiet altid er symmetrisk omkring den lodrette akse x a p x a x x c ()
Matematik for stx C-niveau
 Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
Thomas Jensen og Morten Overgård Nielsen Matematik for stx C-niveau Frydenlund Nu 2. reviderede, udvidede og ajourførte udgave Nu 2. reviderede, udvidede og ajourførte udgave Matema10k Matematik for stx
Studieretningsopgave
 Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Virum Gymnasium Studieretningsopgave Harmoniske svingninger i matematik og fysik Vejledere: Christian Holst Hansen (matematik) og Bodil Dam Heiselberg (fysik) 30-01-2014 Indholdsfortegnelse Indledning...
Stx matematik B maj 2009
 Ib Michelsen Svar stxb maj 2009 1 Stx matematik B maj 2009 Opgave 1 Bestem f ' ( x), idet f (x )=2 x 3 +4 x 2 f ' ( x)=(2 x 3 +4 x 2 )'=(2 x 3 )'+(4 x 2 )'=2 ( x 3 )' +4 ( x 2 )'=2 3 x 3 1 +4 2 x 2 1 =6
Ib Michelsen Svar stxb maj 2009 1 Stx matematik B maj 2009 Opgave 1 Bestem f ' ( x), idet f (x )=2 x 3 +4 x 2 f ' ( x)=(2 x 3 +4 x 2 )'=(2 x 3 )'+(4 x 2 )'=2 ( x 3 )' +4 ( x 2 )'=2 3 x 3 1 +4 2 x 2 1 =6
Eksponentielle funktioner
 Eksponentielle funktioner http://en.wikipedia.org/wiki/rabbits_in_australia 4. udg. 2011 12-12-2011 Eksponentielle funktioner Vækst Udfyld tabellen ved: at skrive begyndelsesværdien b = f(0) = 30 under
Eksponentielle funktioner http://en.wikipedia.org/wiki/rabbits_in_australia 4. udg. 2011 12-12-2011 Eksponentielle funktioner Vækst Udfyld tabellen ved: at skrive begyndelsesværdien b = f(0) = 30 under
4. Snittets kædebrøksfremstilling og dets konvergenter
 Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Dette er den fjerde af fem artikler under den fælles overskrift Studier på grundlag af programmet SKALAGENERATOREN (forfatter: Jørgen Erichsen) 4. Snittets kædebrøksfremstilling og dets konvergenter Vi
Opsætte f.eks. en rejsebeskrivelse med tekst og billede i Draw side 1
 side 1 Hvis man vil lave en opsætning af rejsebeskrivelse og billeder, kan man også gøre det i DRAW. Denne vejledning vil vise hvordan man indsætter hjælpelinjer så man laver en pæn opstilling med billede
side 1 Hvis man vil lave en opsætning af rejsebeskrivelse og billeder, kan man også gøre det i DRAW. Denne vejledning vil vise hvordan man indsætter hjælpelinjer så man laver en pæn opstilling med billede
Matematik Grundforløbet
 Matematik Grundforløbet Mike Auerbach (2) y 2 Q 1 a y 1 P b x 1 x 2 (1) Matematik: Grundforløbet 2. udgave, 2015 Disse noter er skrevet til matematikundervisning i grundforløbet på stx og kan frit anvendes
Matematik Grundforløbet Mike Auerbach (2) y 2 Q 1 a y 1 P b x 1 x 2 (1) Matematik: Grundforløbet 2. udgave, 2015 Disse noter er skrevet til matematikundervisning i grundforløbet på stx og kan frit anvendes
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter (især for B- og A-niveau)
 Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
På opdagelse i Mandelbrot-fraktalen En introduktion til programmet Mandelbrot
 Jørgen Erichsen På opdagelse i Mandelbrot-fraktalen En introduktion til programmet Mandelbrot Hvad er en fraktal? Noget forenklet kan man sige, at en fraktal er en geometrisk figur, der udmærker sig ved
Jørgen Erichsen På opdagelse i Mandelbrot-fraktalen En introduktion til programmet Mandelbrot Hvad er en fraktal? Noget forenklet kan man sige, at en fraktal er en geometrisk figur, der udmærker sig ved
Matema10k. Matematik for hhx C-niveau. Arbejdsark til kapitlerne i bogen
 Matema10k Matematik for hhx C-niveau Arbejdsark til kapitlerne i bogen De følgende sider er arbejdsark og opgaver som kan bruges som introduktion til mange af bogens kapitler og underemner. De kan bruges
Matema10k Matematik for hhx C-niveau Arbejdsark til kapitlerne i bogen De følgende sider er arbejdsark og opgaver som kan bruges som introduktion til mange af bogens kapitler og underemner. De kan bruges
Tilfældige rektangler: Et matematikeksperiment Variable og sammenhænge
 Tilfældige rektangler: Et matematikeksperiment Variable og sammenhænge Baggrund: I de senere år har en del gymnasieskoler eksperimenteret med HOT-programmet i matematik og fysik, hvor HOT står for Higher
Tilfældige rektangler: Et matematikeksperiment Variable og sammenhænge Baggrund: I de senere år har en del gymnasieskoler eksperimenteret med HOT-programmet i matematik og fysik, hvor HOT står for Higher
Projekt 6.7. Beviser for Pythagoras sætning - og konstruktion af animationer
 Projekt 6.7. Beviser for Pythagoras sætning - og konstruktion af animationer Flere beviser for Pythagoras sætning 1 Bevis for Pythagoras sætning ved anvendelse af ensvinklede trekanter... 1 Opgave 1 Et
Projekt 6.7. Beviser for Pythagoras sætning - og konstruktion af animationer Flere beviser for Pythagoras sætning 1 Bevis for Pythagoras sætning ved anvendelse af ensvinklede trekanter... 1 Opgave 1 Et
Differential- ligninger
 Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Differential- ligninger Et oplæg 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der kan gennemgås før man går i gang med en lærebogs fremstilling af emnet differentialligninger Læreren skal
Kapital- og rentesregning
 Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Rentesregning Rettet den 28-12-11 Kapital- og rentesregning Kapital- og rentesregning Navngivning ved rentesregning I eksempler som Niels Oles, hvor man indskyder en kapital i en bank (én gang), og banken
Differentialligninger med TI-Interactive!
 Differentialligninger med TI-Interactive! Jan Leffers (2008) Indholdsfortegnelse Indholdsfortegnelse...3 1. ordens differentialligninger... 4 Den fuldstændige løsning... 4 Løsning med bibetingelse...4
Differentialligninger med TI-Interactive! Jan Leffers (2008) Indholdsfortegnelse Indholdsfortegnelse...3 1. ordens differentialligninger... 4 Den fuldstændige løsning... 4 Løsning med bibetingelse...4
