Numerisk. differentiation. Erik Vestergaard
|
|
|
- Rikke Holmberg
- 7 år siden
- Visninger:
Transkript
1 Numerisk differentiation Erik Vestergaard
2 2 Erik Vestergaard Erik Vestergaard, 25. Billeder: Forside: istock.com/iunewind Side 5: istock.com/cienpies Desuden egne illustrationer
3 Erik Vestergaard 3 Numerisk differentiation I en del situationer har man ikke en forskrift for en funktion. Det kunne for eksempel være et forsøg, hvor man har en række målepunkter. Man kunne da tro, at man er afskåret fra at differentiere, altså finde tangenthældninger. Det er heldigvis ikke tilfældet: man kan benytte numerisk differentiation. For at det skal kunne lykkes på en fornuftig måde, skal datapunkter helst ligge ret tæt og ikke være behæftet med for store usikkerheder eller støj. Lad os tage udgangspunkt i en funktion og forsøge at udvikle en teknik, som giver tilnærmede værdier for differentialkvotienterne i en række punkter. Af definitionen på differentiabilitet ved vi, at en funktion er differentiabel, hvis differenskvotienten har en grænseværdi for x, og differentialkvotenten er da lig med den pågældende grænseværdi: y f ( x+ x) f ( x) () = f '( x) for x x x Sætning Hvis f er en funktion, som er differentiabel i x, så gælder følgende: f ( x+ x) f ( x x) (2) 2 x f '( x ) for x Bevis: Fra definitionen af differentiabilitet ved vi, at grænseværdien af differenskvotienten skal være den samme, uanset om x nærmer sig til fra højre eller fra venstre. I stedet for at sige at x går mod fra venstre, kan vi lige så godt udskifte x med x i (), uden at det ændrer på grænseværdien. Vi har altså: f ( x x) f ( x) (3) x og lægger sammen, så får vi umiddel- Hvis vi ganger () med og ganger (3) med 2 2 bart (2). Detaljerne overlades til læseren. f '( x ) for x Grunden til at vi i det følgende vil bruge grænseværdien (2) fremfor grænseværdien () er, at (2) normalt konvergerer hurtigst af de to. Hermed menes, at udtrykket på venstre side i (2) normalt nærmer sig hurtigere til differentialkvotienten, når x, end den normale differenskvotient gør. Situationen kan ses på grafen på næste side. Vi ønsker en tilnærmet værdi for differentialkvotienten f ( x) i x, dvs. en værdi for hældningen af den røde tangent. Her vil udtrykket på venstre side i (2), som grafisk er hældningen af den grønne sekant, normalt være en bedre tilnærmelse til tangentens hældning, end differenskvotienten er. Denne påstand virker også sandsynlig, når man kigger på grafen på næste side.
4 4 Erik Vestergaard (4) f ( x ) = hældning af den røde linje (5) f ( x+ x) f ( x) = hældning af den blå linje x (6) f ( x) f ( x x) = hældning af den gule linje x f ( x + x) f ( x x) 2 x (7) hældning af den grønne = linje f( x) x x x x x Øvelse 2 Forklar hvorfor (7) er rigtigt, dvs. at udtrykket er lig hældningen af sekanten gennem de to punkter på hver side af x. Vi vil i vore metoder kræve, at datapunkternes x-værdier ligger ligeligt fordelt hen ad x- aksen, dvs. at der er samme skridtlængde overalt. Den vil vi betegne med h. Den kommer til at svare til x ovenfor. For at gøre det mere overskueligt, vælger man ofte at ændre notationen: x-koordinaten for det punkt, vi er i færd med at betragte, vil vi betegne med x. Punkterne til højre for skal have x-koordinater x, x 2,..., mens dem til venstre for skal have x-koordinater x, x 2,... f f f - x -4 x -3 x -2 x - x x x 2 x 3 x 4 h
5 Erik Vestergaard 5 Vi vil endvidere lade f betegne differentialkvotienten i x. Med disse nye betegnelser kommer (5), (6) og (7) til at give anledning til følgende numeriske metoder til bestemmelse af tilnærmede værdier for differentialkvotienten i x : f f (8) f (Forward difference) h f f (9) f (Backward difference) h f f () f (Central difference) 2h Metodernes respektive navne på engelsk er angivet i parentes. Vi ser, at forward difference involverer det betragtede punkt og det næste punkt. Backward difference involverer det betragtede punkt og det forrige punkt. Central difference involverer både det næste og det forrige punkt, men ikke det aktuelle punkt selv. Central difference metoden er normalt klart den mest nøjagtige af de tre. I det næste afsnit vil vi i programmet Excel teste metoderne forward difference og central difference på data fra en kendt funktion. I det efterfølgende afsnit vil vi se på numeriske metoder anvendt på rigtig data fra et forsøg i programmet Logger Pro. Endelig vil vi i sidste afsnit med titlen "Taylorpolynomier og andet godt" otale andre numeriske metoder og hvordan man kan vurdere, hvor nøjagtige metoderne er. Sidste afsnit er ikke specielt rettet mod gymnasieelever, da sværhedsgraden er ret høj.
6 6 Erik Vestergaard Eksperiment i Excel med data fra kendt funktion I denne øvelse skal du teste forskellen på, hvor god metoden central difference er sammenlignet med metoden forward difference i tilfældet, hvor data følger funktionsværdierne for en kendt funktion. Det sætter os nemlig i stand til at sammenligne de numeriske værdier for differentialkvotienterne med de rigtige. Programmet Microsoft Excel er meget velegnet til opgaven. Nedenfor vil jeg give detaljer til, hvordan det udføres for de læsere, som ikke er så rutinerede i brugen af Excel. Vi vil undersøge funktionen f ( x) = x sin( x). Det er et mere eller mindre tilfældigt valg. Vi betragter funktionen i intervallet [,7] og vælger en skridtlængde på,. a) Åben et regneark og skriv i felterne, så det ser ud nogenlunde som nedenfor. Baggrundsfarverne hjælper til at give overblik. b) Vi ønsker at alle tal, som står i kolonnerne fra B til og med G skal vises med 6 decimaler. Det klares ved at markere de seks kolonner i den grå vandrette linje med kolonne bogstaverne og derefter højreklikke, mens cursoren befinder sig et sted over det markerede område. I den fremkomne kontekstmenu vælges Formater celler.
7 Erik Vestergaard 7 c) Under fanen Tal og kategorien Tal vælges antal decimaler til 6. Afslut med OK. d) I kolonne A gør du det samme, bortset fra at antal decimaler sættes til 2. e) Startværdien for x'erne står i felt B3 og skridtlængden står i felt B4. Grunden til at de er skrevet ovenfor det egentlige regneark er, at det så bliver nemmere at foretage ændringer i disse værdier, hvis vi senere vil foretage andre undersøgelser. Start med at skrive =B3 i feltet A8 og tryk Enter. Husk at når man skriver et lighedstegn som det første i et felt, så ved Excel, at man er i gang med at skrive en formel. f) I felt B9 skrives formlen =A8+$B$4 og der afsluttes med Enter.
8 8 Erik Vestergaard g) Vi skal nu til at nedkopiere. Det betyder, at vi sparer arbejdet med at gentage formlerne i hvert felt fra A til A78. Bemærk, at det var vigtigt, at vi i formlen i felt A9 anbragte dollartegn, da det sikrer at feltet B4 ikke ændrer sig ved nedkopiering. Derimod skal feltet A8 i formlen ændres til A9, A, etc. når vi nedkopierer. Derfor ingen dollartegn her! Man nedkopierer ved at lade cursoren vandre ned i højre hjørne af feltet indtil cursoren bliver til et sort plus-tegn. Når cursoren ser således ud, trækker du nedad ind til og med felt A78. h) Du har nu tallene fra til 7 i skrift på, i kolonne A. Vi skal derefter til kolonne B. Her ønsker vi de tilhørende funktionsværdier for funktionen f ( x) = x sin( x). Anbring cursoren i feltet B8 og skriv formlen =A8*sin(A8) og afslut med Enter. Husk at feltet A8 indeholder x-værdien. i) Nedkopier feltet B8 indtil felt B78. j) Vi skal have de korrekte differentialkvotienter i kolonne C. Vi har på forhånd regnet ud, at f ( x) = sin( x) + x cos( x). Derfor skriver du i feltet C8 følgende formel: =sin(a8)+a8*cos(a8), trykker Enter og nedkopierer derefter til feltet C78. k) Vi skal nu have udregnet værdierne for differentialkvotienterne beregnet ved hjælp af forward difference metoden. I felt D8 skriver du formlen =(B9-B8)/$B$4, trykker Enter og nedkopierer derefter til feltet D77 (ikke D78!).
9 Erik Vestergaard 9 l) Bemærk lige fra forrige punkt, at formlen =(B9-B8)/$B$4 er logisk: Den tilnærmede værdi for differentialkvotienten i en given x-værdi er forskellen mellem funktionsværdien et skridt længere fremme og funktionsværdien i den aktuelle x-værdi og så divideret med skridtlængden, som står i feltet B4. Men vi skal have beregnet afvigelsen i forhold til den rigtige værdi for differentialkvotienten. Derfor skriver du i feltet E8 formlen =D8-C8, trykker Enter og nedkopierer ned til E77. m) Vi er nu klar til den numeriske metode kaldet central difference, som vi formoder e r mere nøjagtig end forward difference metoden. Bemærk i øvrigt, at der er tilføjet et 3-tal i navnet. Det skyldes, at der findes en central difference metode for hvert ulige tal. I de metoder med højere nummer medtages blot flere funktionsværdier på højre og venstre side af den aktuelle x-værdi. I feltet F9 (ikke F8!) skriver du følgende formel: =(B-B8)/(2*$B$4), trykker på Enter og nedkopierer til feltet F77. Grunden til, at du skal starte i feltet F9 og ikke allerede i felt F8 er naturligvis, at der ikke er nogen funktionsværdi før den første x-værdi, og det kræves jo af metoden. Så vi starter altså i næste x-værdi! n) Tilsvarende som under punkt l), kan du nu bestemme afvigelserne ved i feltet G9 af skrive formlen =F9-C9 og derefter nedkopiere
10 Erik Vestergaard o) Nu kan du inspicere og sammenligne fejlene i de to numeriske metoder i tilfældet med denne funktion ved at kigge i tallene i kolonne E og G. Det kan dog give et større overblik, hvis man laver en graf over fejlene som funktion af x-værdien. Det kan du gøre ved at markere alle felterne fra A9 til og med A77, holde Ctrl-tasten nede, mens du også markerer felterne fra E9 til og med E77 og felterne G9 til og med G77 og derefter vælge menuen Indsæt > Punktdiagram (kun med datamærker). Så får du en meget visuel indikation, at metoden central difference 3 er meget mere nøjagtig end forward difference. Efter lidt formatering og retten til, kan det komme til at se ud som nedenfor Afvigelse i differentialkvotient,3,25,2,5,,5, -,5 -, -,5 -,2 Fejl i de to numeriske metoder Forward difference Central difference x p) Man kan naturligvis også ønske at tegne grafen for de numeriske differentialkvotienter som funktion af x-værdien. Det kan gøres på lignende måde som under punkt o). Detaljerne overlades til læseren.
11 Erik Vestergaard Analyse af eksperimentel data med støj i Logger Pro I mange anvendelser af numerisk differentiation har man blot en liste af datapunkter fra et forsøg. Udover at disse datapunkter ikke nødvendigvis behøver følge en teoretisk kurve, er de desuden ofte behæftet med støj/usikkerhed. Vi kan dog gøre brug af numerisk differentiation alligevel. Hvilken metode, der er mest velegnet, afhænger dog af datapunkternes forløb og graden af støj. Der findes i øvrigt adskilligt flere metoder til bestemmelse af numeriske værdier for differentialkvotienter end de tre, der er omtalt tidligere i dette dokument. Lad os sige, at vi har optaget målinger af PH-værdien under en titreringsøvelse, hvor vi løbende tilsætter dråber af NaOH til en opløsning af H 3 PO 4. Vi ønsker at bestemme ækvivalenspunktet så nøjagtigt som muligt. Dette punkt findes, hvor hældningskoefficienten på kurven er størst mulig. Man indser, at det svarer til at finde det sted, hvor differentialkvotienten har maksimum. I det følgende antages, at data er optaget ved hjælp af for eksempel en PH-elektrode og en dråbetæller tilsluttet en LabQuest, samt at data er registreret i de to første søjler i software programmet Logger Pro. Logger Pro har indbygget faciliteter til numerisk differentiation: a) Vælg menuen Data > Ny beregnet kolonne I den fremkommende dialogboks anfører du navne. Dernæst trykkes på knappen Funktioner.
12 2 Erik Vestergaard b) I funktionsmenuen vist nedenfor vælges punktet regning > derivative. Sidstævnte er det engelske ord for differentialkvotient. c) Efter punkt b) er der skrevet følgende i feltet Udtryk i dialogboksen: derivative(). Mens cursoren står midt mellem parenteserne, skal du have fortalt, hvad der skal differentieres. Det kan gøres ved at trykke på knappen Variabler, hvorefter der vælges "PH" i dropdown-menuen da det jo er navnet på vore funktionsværdier! Herefter skulle det gerne se således ud i feltet Udtryk:
13 Erik Vestergaard 3 d) Vi skal have valgt det antal decimaler, som tallene i vores nye kolonne skal vises med. Tryk på fanen Indstillinger og vælg mindst 4, som vist nedenfor. Afslut ved at trykke på knappen Udført. e) Du skal nu vælge hvilken numerisk metode, som du vil bruge til at differentiere med. Det gøres i menuen Filer > Indstillinger for efterfuldt af navnet på filen.
14 4 Erik Vestergaard f) Hvis du som nedenfor vælger 3 i dropdown-menuen for Antal punkter for afledt beregning, så anvendes faktisk metoden central difference 3, som vi har behandlet tidligere i denne note. Hvis du gerne vil overbevise dig om rigtigheden heri, kan du jo for eksempel kopiere værdierne fra de to første søjler i Logger Pro over i et Excel regneark og så selv udregne differentialkvotienterne ved hjælp af central difference 3 metoden for at se, at det giver det samme som Logger Pro giver i tredje kolonne - som omtalt i afsnittet Eksperiment i Excel med data fra kendt funktion. g) Du mangler at få vist grafen for differentialkvotienterne. Det gøres meget nemt i Logger Pro ved at klikke et sted på anden-aksen. Herved får du adgang til en lille menu, hvor du vælger punktet Mere. I den nye dialogboks skal du afkrydse feltet Diff, som jo er navnet på vores kolonne med differentialkvotienter!
15 Erik Vestergaard 5 h) Når du har afsluttet med OK, får du grafen for differentialkvotienterne vist sammen med grafen for PH værdierne. i) Datapunkterne i den nye graf kan synes noget store. Det kan heldigvis ændres ved at dobbeltklikke på overskriften i kolonne 3. Herved popper en dialogboks op, hvor du kan indstille datapunkterne til en rund cirkel og størrelsen af punkterne som Meget lille. Afslut med at trykke på knappen Udført.
16 6 Erik Vestergaard j) Ækvivalenspunkterne kan nu nemmere aflæses, ved at kigge på den differentierede graf. Bemærk, at du sagtens kan ombestemme dig og vælge en anden numerisk metode ved at gå ind i menuen Filer > Indstillinger for k) Hvis støjen er så stor, at man ikke synes de numeriske metoder er tilstrækkelige, kan man også foretage udglatning. Man kan for eksempel lave en ny beregnet kolonne og kalde den "Udglat". Tryk på knappen Funktioner og vælg smoothave. Tryk derefter på Variabler knappen og vælg Diff var det er navnet på den kolonne, vi ønsker udglattet. l) Bemærk, at du kan styre graden af udglatning via menuen Filer > Indstillinger for under punktet Antal punkter for smoothing beregning:
17 Erik Vestergaard 7 m) Herefter kan du nemt få vist den udglattede graf ved at klikke på anden-aksen Lad os stoppe databehandlingen i Logger Pro her.
18 8 Erik Vestergaard Taylorpolynomier og flere differensmetoder Dette afsnit og de følgende er dedikeret til folk, som vil have et lidt større overblik over området med numerisk differentiation. Stoffet er nok i overkanten af, hvad de fleste elever i gymnasiet med rimelighed kan tilegne sig. Det er derfor for viderekomne. Lad f være en funktion, som er differentiabel i x. Fra gymnasiet kender vi ligningen for tangenten til grafen for f i punktet x : () y= f ( x) ( x x) + f ( x) Vi ved, at tangenten til grafen for f i x tilnærmer funktionen omkring dette punkt. Hvis vi kigger på det fra et funktionssynspunkt, så kan vi definere følgende funktion: ( ) ( ) ( ) ( ) (2) P x = f x + f x x x som er et førstegradspolynomium i x husk at x er konstant! Men som nævnt er P ( x ) kun en tilnærmelse til f ( x ). Forskellen mellem f ( x ) og P ( x ) vil vi betegne R ( x ). Det betegnes også restleddet. Vi har dermed: f ( x) = f ( x ) + f ( x ) ( x x ) + R ( x) (3) Vi er interesseret i at få lidt mere styr på dette restled. Kan vi sætte en øvre grænse for, hvor stor det kan være? Svaret er bekræftende, hvis vi antager, at funktionen er to gange kontinuert differentiabel i et interval omkring x. Vi skal have fat i den anden afledede af funktionen. Men før vi ser på den, skal vi formulere og bevise en berømt og smuk sætning, som ofte viser sig velegnet i beviser. Sætning 3 (Rolles sætning) Lad f være en funktion, som er kontinuert i det lukkede interval [ a, b ], differentiabel i det tilsvarende åbne interval ] a, b [ og som opfylder at f ( a) = f ( b) =. Så findes der et c ] a, b[, så f ( c) =. Bevis: Rent intuitivt virker sætningen indlysende, når man kigger på en figur. Hvis grafen for f har endepunkter på x-aksen, så må der være mindst et sted imellem, hvor der er vandret tangent. I tilfældet på figuren er der endda to mulige valg for c. a c b
19 Erik Vestergaard 9 Vi vil dog alligevel give et formelt bevis. Hvis funktionen er identisk nul i hele det lukkede interval [ a, b ], så er f ( x) lig med for alle x ] a, b[. I det tilfælde kan ethvert punkt i det åbne interval vælges som c. Hvis f ikke er konstant lig med i det lukkede interval, så bruger vi kontinuiteten af f til at konkludere, at der må findes et maksimum og et minimum for f i [ a, b ]. De kan ikke begge være, eftersom f ikke er konstant lig med. Det punkt på x-aksen, hvori der er et maksimum eller et minimum, som er forskellig fra, kan bruges som c. Dels er der klart vandret tangent i dette punkt og dels er det et indre punkt i intervallet. Det sidste følger af, at funktionsværdien er her, mens funktionsværdierne i endepunkterne er. Sætning 4 (Taylors formel for n= 2 ) Antag at funktionen er to gange kontinuert differentiabel i et interval I, hvor x I. For ethvert x I findes da et c mellem x og x, så (4) f ( x) = f ( x ) + f ( x ) ( x x ) + f ( c) ( x x ) 2 2 Bevis: Ifølge (2) kan (4) også udtrykkes ved (5) f ( x) = P ( x) + f ( c) ( x x ) 2 hvor P er det approksimerende førstegradspolynomium. Lad x og x være givet. Vi vil da definere en størrelse K ved f ( x) P ( x) (6) K = 2 ( x x ) Dermed haves: (7) Vi indfører nu en hjælpefunktion: f ( x) = P ( x) + K ( x x ) 2 2 (8) H ( t) = f ( t) P ( t) K ( t x ) 2 For det første ser vi, at K ikke afhænger af t, så den vil fungere som en konstant i hjælpefunktionen. Lad os differentiere hjælpefunktionen et par gange: (9) H ( t) = f ( t) P ( t) 2 K ( t x) (2) H ( t) = f ( t) P ( t) 2 K = f ( t) 2K I (2) har vi udnyttet, at P er et førstegradspolynomium og derfor giver, når den differentieres to gange. Lad os indsætte x i både H og H : (2) 2 H ( x ) = f ( x ) P ( x ) K ( x x ) = f ( x ) P ( x ) = H ( x ) = f ( x ) P ( x ) 2 K ( x x ) = f ( x ) P ( x ) = (22) Af (7) og (8) får vi at H( x ) =. Da hjælpefunktionen er i både x og x, kan vi bruge Rolles sætning til at konkludere, at der findes et c mellem x og x, så H ( c ) =.
20 2 Erik Vestergaard Vi kan gentage successen med H. Den er nemlig nul i både c og x ifølge (22). Dermed kan Rolles sætning bruges igen. Vi slutter at der findes et c mellem c og x, så H ( c) =. Ifølge (2) betyder det, at f ( c) 2K = K = 2 f ( c). Dnne værdi 2 kan indsættes i (7), hvoraf vi får f ( x) = P ( x) + 2 f ( c) ( x x) og dermed (4), som ønsket. Værdien c ligger desuden klart mellem x og x. Den bør bemærkes, at c normalt afhænger af x og x. At sætningen alligevel er meget brugbar kan demonstreres ved et eksempel. Eksempel 5 Betragt funktionen f ( x) = sin( x). Når vi differentierer et par gange, får vi umiddelbart følgende: f ( x) = cos( x) og f ( x) = sin( x). Vi ønsker at udregne det approksimerende. gradspolynomium i punktet x = π 4 : som giver: f ( x ) = f ( ) = sin( ) = f ( x ) = f ( ) = cos( ) = π π 2 π π , P ( x) = f ( ) + f ( ) ( x ) = + ( x ) = x+ ( ),77x+,57 π π π 2 2 π 2 2 π Spørgsmålet er hvor præcis approksimationen er, hvis man ønsker at indsætte en x værdi i P ( x ) fremfor at indsætte i f ( x ) selv? Lad os sige, at x ligger stykket h fra x, dvs. at h= x x. Vi kan vurdere restleddets numeriske størrelse idet vi bemærker, at sinus altid ligger mellem - og ( ) 2 max ( ) = 2 max sin( ) = 2 c mellem x og x c mellem x og x R x f c x x c h h Fejlen er altså højest af størrelsen 2 2 h. Situationen er illustreret på figuren nedenfor. P( x) f ( x) /4 h x Det er klart at matematikere ikke stiller sig til tåls med at approksimere en funktion med et. gradspolynomium. De vil automatisk tage skridtet videre: Kunne vi ikke approksimere funktionen med et polynomium af højere grad? Det leder os frem til den generelle formel for Taylorpolynomiet.
21 Erik Vestergaard 2 Sætning 6 (Taylors formel) Lad f være en funktion, som er n+ gange kontinuert differentiabel i et interval I, hvor x I. For ethvert x I findes da et c mellem x og x, så ( n) f ( x) f ( x) 2 f ( x) f ( x) = f ( x) + ( x x) + ( x x) + + ( x x)! 2 n! ( n+ ) f ( c) + ( x x ) ( n+ )! n+ n Bevis: Sætningen kan bevises analogt til den måde vi beviste sætning 4 på. Vi vil ikke give detaljer her. Vi kan dele udtrykket i sætning 6 op i to dele: f ( x) = P ( x) + R ( x), hvor n n (23) (24) ( n) f ( x) f ( x) 2 f ( x) Pn ( x) = f ( x) + ( x x) + ( x x) + + ( x x)! 2 n! ( n+ ) f ( c) n+ Rn ( x) = ( x x) ( n+ )! n Her kaldes Pn ( x ) for Taylorpolynomiet af orden n for f ( x ), med udviklingspunkt x. Størrelsen kan også betegnes det approksimerende polynomium af højst n'te grad for f ( x ) i punktet x. Leddet Rn ( x ) kaldes for restleddet. Vi skal kigge på et eksempel. Eksempel 7 I eksempel 5 tilnærmede vi sinus-funktionen med et approksimerende. gradspolynomium i punktet x = π 4. Nu vil vi bestemme det approksimerende 3. gradspolynomium til f ( x) = sin( x) i punktet x =. Vi differentierer fire gange: (4) f ( x) = cos( x), f ( x) = sin( x), f ( x) = cos( x), f () = sin( x) Hvilket med x = indsat giver følgende værdier: f () = sin() =, f () = cos() =, f () = sin() =,, f () = cos() = Vi har dermed: f () f () f () P3 ( x) = f () + ( x ) + ( x ) + ( x )! 2! 3! 2 3 = + x+ x + x! 2! 3! = x 6 x 3 2 3
22 22 Erik Vestergaard f ( x) - P x 3( ) Figuren viser, at det approksimerende tredjegradpolynomium giver en meget fin tilnærmelse til sinus-funktionen, især i nærheden af udviklingspunktet x =. Afvigelsen er bestemt ved restleddet, som vi kan vurdere lidt på samme måde som i eksempel 5: R x f c x x c h h (4) ( ) max ( ) = max sin( ) = ! c mellem og x c mellem og x Vi slutter eksemplet her. Grunden til, at vi har gennemgået teorien for Taylorpolynomierne ovenfor er, at vi kan bruge dem til at udvikle nye metoder til numerisk differentiation. Lad os kigge på Taylorpolynomiet for funktionen f i punktet x og indsætte forskellige værdier for x omkring x, nærmere bestemt x 2 h, x h, x, x+ h og x+ 2h. Det giver følgende: (4) f ( x) f ( x) 2 f ( x) 3 f ( x) 4 f ( x 2 h) = f ( x) + ( 2 h) + ( 2 h) + ( 2 h) + ( 2 h) +! 2! 3! 4! (4) f ( x) f ( x) 2 f ( x) 3 f ( x) 4 f ( x h) = f ( x) + ( h) + ( h) + ( h) + ( h) +! 2! 3! 4! (4) f ( x ) f ( x ) f ( x) 3 f ( x) 4 = ! 2! 3! 4! 2 ( ) f ( x) f x (4) f ( x) f ( x) 2 f ( x) 3 f ( x) 4 f ( x+ h) = f ( x) + h+ h + h + h +! 2! 3! 4! (4) f ( x) f ( x) 2 f ( x) 3 f ( x) 4 f ( x+ 2 h) = f ( x) + (2 h) + (2 h) + (2 h) + (2 h) +! 2! 3! 4! Man kunne nu få den gode idé at gange den første ligning med a 2, den næste ligning med a, den midterste ligning med a og de to efterfølgende ligninger med henholdsvis a og a 2 og derefter lægge alle ligningerne sammen! Derefter kunne man forsøge at bestemme koefficienterne a 2, a, a, a, a2, så funktionsværdien i x, og alle afledede i x op til og med 4. orden går ud, med undtagelse af den første afledede, hvis koefficient vi vil have til at give h. Vi ønsker altså at finde koefficienter a 2, a, a, a, a2, så følgende er opfyldt:
23 Erik Vestergaard 23 (25) a f ( x 2 h) + a f ( x h) + a f ( x ) + a f ( x + h) + a f ( x + 2 h) 2 2 = f ( x ) + h f ( x ) + f ( x ) + f ( x ) + f ( x ) + rest (4) Størrelsen rest er en linearkombination af de restled, der ifølge sætning 6 med n= 4, er på følgende form, hvor c i ligger mellem x og x+ i h for alle i= 2,,,, 2 : (26) (5) (5) (5) f ( c 2) 5 f ( c ) 5 f ( c) 5 2 ( 2 ) ( ) rest = a h + a h + a 5! 5! 5! (5) (5) f ( c) 5 f ( c2) 5 2 (2 ) + a h + a h 5! 5! 5 h 5 (5) 5 (5) 5 (5) = ( 2) a 2 f ( c 2) + ( ) a f ( c ) + a f ( c) 5! 5 (5) 5 (5) + a f ( c) + 2 a2 f ( c2) Lad os vende tilbage til ligningssystemet. Opgaven består i at løse 5 lineære ligninger med 5 ubekendte. Ligningssystemet kan meget overskueligt skrives på matrix-form på følgende måde, hvor koefficienterne a 2, a, a, a, a2 altså er de ubekendte: (27) a 2 ( 2) 2 a ( 2) ( ) 2 a = ( 2) ( ) 2 a ( 2) ( ) 2 a 2 Detaljerne overlades til læseren. Vi regner videre og får: (28) a a 4 4 a = 8 8 a 6 6 a 2 Det viser sig, at ligningssystemet har følgende løsning: a =, a =, a =, a =, a = 2 2 (29) Lad os vende tilbage til leddet rest fra (26). Vi ved nu hvad koefficienterne er lig med. (3) 5 h 5 (5) 5 2 (5) 5 (5) rest = ( 2) 2 f ( c 2) + ( ) ( 3) f ( c ) + f ( c) 5! 5 2 (5) 5 (5) + 3 f ( c ) + 2 ( 2) f ( c2)
24 24 Erik Vestergaard 5 Lad os skrive rest på formen rest= k h, hvor k er en konstant, for at fremhæve afhængigheden af skridtlængden h. Hvis vi benytter den korte notation f i for f ( x+ i h) og f for f ( x), så bliver (25) til følgende: f + f f + f = f h k h Ved at dividere med h på begge sider og flytte restleddet over, får vi det endelige udtryk for den metode, som går under navnet 5-point Central difference, fordi den involverer fem punkter (hvor det ene godt nok er ): (3) som også kan skrives: (32) f 2 3 f 3 f 2 f2 f + + = + k h h f f + 8 f 8 f + f 2h 2 2 = + k h Bemærkning Desværre afhænger leddet rest i (3) af den femte afledede i fem forskellige i øvrigt ukendte punkter. Det viser sig imidlertid, at man kan udskifte alle de fem afledede med en femte afledet evalueret i det samme punkt. Det omtalte fælles punkt vil vi 5 (5) betegne c. Derved bliver restleddet til: rest= 3 h f ( c). Det fælles punkt er også ukendt, men vi ved, at det skal ligge imellem x 2h og x+ 2h. Derved får vi den kortfattede formel: (33) f 2 8 f 8 f f2 4 (5) f + + = + h f ( c) 3 2h hvor c ] x 2 h, x+ 2 h[ eller c ] x 2, x2 [, hvis man foretrækker notationen fra side 4 tidligere i denne note. Forudsætningen for ovenstående er, at funktionen f skal være 5 gange kontinuert differentiabel i et interval I, som indeholder de fem punkter, som vi benytter: x 2, x, x, x, x2. Med det mere præcise restled i (33) fremfor (32) kan vi nemmere foretage vurderinger af den begåede fejl, lidt som vi gjorde tidligere i eksempel 5 og eksempel 7. At restleddet kan skrives på formen 4 (5) 3 h f ( c) i (33) fremgår ikke direkte af ovenstående. Restleddet kan imidlertid fås frem, hvis man tager et helt andet udgangspunkt end vi har taget ovenfor: Hvis man i stedet for Taylorpolynomier bruger interpolationspolynomier på Newtons form, kan man udlede det. Det vil føre for vidt at komme ind på det her. Man kan læse om metoden i [2] fra side 35. På side 79 omtales restleddet. Central Difference formler Vi har allerede set eksempler på to af den slags, som betegnes Central difference metoder. Den første er () side 5 og den anden er (33) ovenfor. Ordet "central" går på, at man benytter funktionsværdier i punkter, som ligger symmetrisk omkring det punkt x, hvori man ønsker den numeriske differentialkvotient. Det giver den bedste tilnærmelse.
25 Erik Vestergaard 25 I Wikipedia (se linket [3]), kan man finde en række central difference-formler. Omskrevet og med restled ser de således ud: f f 2 f = 6 h f ( c) 2h f 2 8 f 8 f f2 4 (5) f + + = + 3 h f ( c) 2h f 3 9 f 2 45 f 45 f 9 f2 f3 6 (7) f = 4 h f ( c) 6h 3 f 4 32 f 3 68 f f 672 f 68 f2 32 f3 3 f4 8 (9) f = + h f ( c) 63 84h I nævnte rækkefølge har de navnene 3-punkt central difference, 5-punkt central difference, 7-punkt central difference og 9-punkt central difference. På samme hjemmeside kan man også finde ikke-centrerede differensmetoder, og endda også formler for højere afledede. Savitsky-Golay filtre Alle de metoder, som blev udviklet med Taylorpolynomier i forrige afsnit, har de egenskaber, at de er eksakte for alle polynomier af grad op til og med ordenen af metoden. Således er 3-punkt central difference eksakt for polynomier med grad op til og med punkt central difference er eksakt for polynomier af grad op til og med 4, etc. Denne påstand ses direkte af restleddets udseende. Det er det maksimalt opnåelige for det antal punkter, som er involveret i de enkelte metoder. Man skulle derfor tro, at man havde at gøre med i enhver henseende optimale numeriske metoder. Det viser sig imidlertid, at metoderne er temmelig følsomme, når de anvendes på hurtigt oscillerende funktioner. Derfor er der blevet udviklet numeriske metoder, som har en bedre egenskab her. En familie af disse er de såkaldte Savitsky-Golay filtre. Vi skal ikke gå i detaljer med dem her, blot henvise til Wikipedia i [4], hvor nedenstående metoder kan findes. Begge er punktsmetoder. Den første har orden O( h ), mens den anden har orden O( h ) : f 3 f 2 f f + f + 2 f + 3 f 28h f 22 f 67 f 58 f + 58 f+ 67 f 22 f 252h Disse filter har desuden ofte en udglattende virkning på data. Løst sagt er de blevet udledt ved at anvende foldning og tilnærme et antal datapunkter med et polynomium af relativ lav grad under anvendelse af mindste kvadraters metode.
26 26 Erik Vestergaard Glatte støj-robuste differentiatorer Nogle andre metoder, jeg er faldet over, er metoder udviklet af Pavel Holoborodko. De kan findes på hans hjemmeside [5]. Jeg vil give hans bud på to 7-punktsmetoder, den 2 4 første af orden O( h ), den anden af orden O( h ) : f f 6 f 4 f + 4 f + 6 f + f 28h f 5 f 2 f 39 f + 39 f + 2 f 5 f 96h Der kan siges meget mere om dette emne med numerisk differentiation. Vi afslutter dog diskussionen af emnet her. Litteratur [] Helge Elbrønd Jensen m. fl. Matematisk analyse. 4. udgave. Institut for matematik, Danmarks Teknisk Universitet, 2. [2] Ward Cheney, David Kincaid. Numerical Mathematics and Computing. Fourth Edition. Brooks/Cole Publishing Company, 999. Links [3] Wikipedia om Finite Differences: [4] Wikipedia on Savitsky-Golay filter: [5] Pavel Holoborodko om Smooth noise-robust differentiators:
Excel tutorial om lineær regression
 Excel tutorial om lineær regression I denne tutorial skal du lære at foretage lineær regression i Microsoft Excel 2007. Det forudsættes, at læseren har været igennem det indledende om lineære funktioner.
Excel tutorial om lineær regression I denne tutorial skal du lære at foretage lineær regression i Microsoft Excel 2007. Det forudsættes, at læseren har været igennem det indledende om lineære funktioner.
Matematik og samfundsfag Gini-koefficienten
 Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Erik Vestergaard www.matematikfysik.dk Matematik og samfundsfag Gini-koefficienten Den såkaldte Gini-koefficient, introduceret i 92 i en artikel af den italienske statistiker, demograf og sociolog Corrado
Excel tutorial om indekstal og samfundsfag 2008
 Excel tutorial om indekstal og samfundsfag 2008 I denne note skal vi behandle data fra CD-rommen Samfundsstatistik 2008, som indeholder en mængde data, som er relevant i samfundsfag. Vi skal specielt analysere
Excel tutorial om indekstal og samfundsfag 2008 I denne note skal vi behandle data fra CD-rommen Samfundsstatistik 2008, som indeholder en mængde data, som er relevant i samfundsfag. Vi skal specielt analysere
Introduktion til differentialregning 1. Jens Siegstad og Annegrethe Bak
 Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Introduktion til differentialregning 1 Jens Siegstad og Annegrete Bak 16. juli 2008 1 Indledning I denne note vil vi kort introduktion til differentilregning, idet vi skal bruge teorien i et emne, Matematisk
Noter til Computerstøttet Beregning Taylors formel
 Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
Noter til Computerstøttet Beregning Taylors formel Arne Jensen c 23 1 Introduktion I disse noter formulerer og beviser vi Taylors formel. Den spiller en vigtig rolle ved teoretiske overvejelser, og også
i x-aksens retning, så fås ). Forskriften for g fås altså ved i forskriften for f at udskifte alle forekomster af x med x x 0
 BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
BAndengradspolynomier Et polynomium er en funktion på formen f ( ) = an + an + a+ a, hvor ai R kaldes polynomiets koefficienter. Graden af et polynomium er lig med den højeste potens af, for hvilket den
Differentialregning. Ib Michelsen
 Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Differentialregning Ib Michelsen Ikast 2012 Forsidebilledet Tredjegradspolynomium i blåt med rød tangent Version: 0.02 (18-09-12) Denne side er (~ 2) Indholdsfortegnelse Introduktion...5 Definition af
Taylorudvikling I. 1 Taylorpolynomier. Preben Alsholm 3. november Definition af Taylorpolynomium
 Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Taylorudvikling I Preben Alsholm 3. november 008 Taylorpolynomier. Definition af Taylorpolynomium Definition af Taylorpolynomium Givet en funktion f : I R! R og et udviklingspunkt x 0 I. Find et polynomium
Pointen med Differentiation
 Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Pointen med Differentiation Frank Nasser 20. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Matematisk modellering og numeriske metoder. Lektion 16
 Matematisk modellering og numeriske metoder Lektion 16 Morten Grud Rasmussen 6. november, 2013 1 Interpolation [Bogens afsnit 19.3 side 805] 1.1 Interpolationspolynomier Enhver kontinuert funktion f på
Matematisk modellering og numeriske metoder Lektion 16 Morten Grud Rasmussen 6. november, 2013 1 Interpolation [Bogens afsnit 19.3 side 805] 1.1 Interpolationspolynomier Enhver kontinuert funktion f på
1. Installere Logger Pro
 Programmet Logger Pro er et computerprogram, der kan bruges til at opsamle og behandle data i de naturvidenskabelige fag, herunder fysik. 1. Installere Logger Pro Første gang du installerer Logger Pro
Programmet Logger Pro er et computerprogram, der kan bruges til at opsamle og behandle data i de naturvidenskabelige fag, herunder fysik. 1. Installere Logger Pro Første gang du installerer Logger Pro
Funktioner. 3. del Karsten Juul
 Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
PeterSørensen.dk : Differentiation
 PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
PeterSørensen.dk : Differentiation Betydningen af ordet differentialkvotient...2 Sekant...2 Differentiable funktioner...3 Bestemmelse af differentialkvotient i praksis ved opgaveløsning...3 Regneregler:...3
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 35-del 1, 2010 Redigeret af Jessica Carter efter udgave af Hans J. Munkholm 1 Nogle talmængder s. 4 N = {1,2,3, } omtales som de naturlige tal eller de positive heltal. Z =
MM501 forelæsningsslides uge 35-del 1, 2010 Redigeret af Jessica Carter efter udgave af Hans J. Munkholm 1 Nogle talmængder s. 4 N = {1,2,3, } omtales som de naturlige tal eller de positive heltal. Z =
Differential- regning
 Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Differential- regning del f(5) () f f () f ( ) I 5 () 006 Karsten Juul Indhold 6 Kontinuert funktion 7 Monotoniforhold7 8 Lokale ekstrema44 9 Grænseværdi5 Differentialregning del udgave 006 006 Karsten
Erik Vestergaard 1. Opgaver. i Lineære. funktioner. og modeller
 Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Erik Vestergaard www.matematikfsik.dk Opgaver i Lineære funktioner og modeller Erik Vestergaard www.matematikfsik.dk Erik Vestergaard, Haderslev. www.matematikfsik.dk Teknik. Aflæse forskrift fra graf...
Differential- regning
 Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
Differential- regning del () f () m l () 6 Karsten Juul Indhold Tretrinsreglen 59 Formler for differentialkvotienter64 Regneregler for differentialkvotienter67 Differentialkvotient af sammensat funktion7
En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby
 24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
24 En differentiabel funktion hvis afledte ikke er kontinuert Søren Knudby Det er velkendt for de fleste, at differentiabilitet af en reel funktion f medfører kontinuitet af f, mens det modsatte ikke gælder
For at få tegnet en graf trykkes på knappen for graftegning. Knap for graftegning
 Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Graftegning på regneark. Ved hjælp af Excel regneark kan man nemt tegne grafer. Man åbner for regnearket ligger under Microsoft Office. Så indtaster man tallene fra tabellen i regnearkets celler i en vandret
Taylor-polynomier. John V Petersen
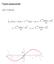 Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Taylor-polynomier John V Petersen Taylor-polynomier 2018 John V Petersen art-science-soul Indhold 1. Indledning... 4 2. Udledning af Sætning om Taylor polynomiet... 4 3. Sætning og Definition af Taylor
Newton-Raphsons metode
 Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Newton-Raphsons metode af John V. Petersen Indhold Indledning: Numerisk analyse og Newton-Raphsons metode... 2 Udlede Newtons iterations formel... 2 Sætning 1 Newtons metode... 4 Eksempel 1 konvergens...
Taylor s approksimationsformler for funktioner af én variabel
 enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
enote 4 1 enote 4 Taylor s approksimationsformler for funktioner af én variabel I enote 19 og enote 21 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier i
Differentiation. Frank Nasser. 11. juli 2011
 Differentiation Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Differentiation Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Taylor s approksimationsformler for funktioner af én variabel
 enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
enote 17 1 enote 17 Taylor s approksimationsformler for funktioner af én variabel I enote 14 og enote 16 er det vist hvordan funktioner af én og to variable kan approksimeres med førstegradspolynomier
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
MM50 forelæsningsslides uge 36, 2009 Produceret af Hans J. Munkholm Nogle talmængder s. 3 N = {, 2, 3, } omtales som de naturlige tal eller de positive heltal. Z = {0, ±, ±2, ±3, } omtales som de hele
En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau)
 Matematik i WordMat En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau) Indholdsfortegnelse 1. Introduktion... 3 2. Beregning... 4 3. Beregning med brøker...
Matematik i WordMat En lille vejledning til lærere og elever i at bruge matematikprogrammet WordMat (begynderniveau) Indholdsfortegnelse 1. Introduktion... 3 2. Beregning... 4 3. Beregning med brøker...
Analyse af en lineær regression med lav R 2 -værdi
 Analyse af en lineær regression med lav R 2 -værdi Denne gennemgang omhandler figur 13 i Regn med biologi. Man kan sagtens lave beregninger på egne data. Forsøgsmæssigt kræver det bare en tommestok tapet
Analyse af en lineær regression med lav R 2 -værdi Denne gennemgang omhandler figur 13 i Regn med biologi. Man kan sagtens lave beregninger på egne data. Forsøgsmæssigt kræver det bare en tommestok tapet
matx.dk Differentialregning Dennis Pipenbring
 mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
Differentialregning Infinitesimalregning
 Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Udgave 2.1 Differentialregning Infinitesimalregning Noterne gennemgår begreberne differentialregning, og anskuer dette som et derligere redskab til vækst og funktioner. Noterne er supplement til kapitel
Matematisk modellering og numeriske metoder. Lektion 17
 Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Matematisk modellering og numeriske metoder Lektion 1 Morten Grud Rasmussen. december 16 1 Numerisk integration og differentiation 1.1 Simpsons regel Antag, at vi har en funktion f på intervallet I = [a,
Projekt 2.2 Omvendt funktion og differentiation af omvendt funktion
 ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
ISBN 978877664974 Projekter: Kapitel. Projekt. Omvendt funktion og differentiation af omvendt funktion Projekt. Omvendt funktion og differentiation af omvendt funktion Vi har i Bbogens kapitel 4 afsnit
Differentiation af sammensatte funktioner
 1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
1/7 Differentiation af sammensatte funktioner - Fra www.borgeleo.dk En sammensat funktion af den variable x er en funktion, vor x først indsættes i den såkaldte indre funktion. Resultatet fra den indre
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
er den radioaktive kildes aktivitet til tidspunktet t= 0, A( t ) er aktiviteten til tidspunktet t og k er henfaldskonstanten.
 Fysikøvelse Erik Vestergaard www.matematikfysik.dk Radioaktive henfald Formål Formålet i denne øvelse er at eftervise henfaldsloven A( t) = A0 e kt, hvor A 0 er den radioaktive kildes aktivitet til tidspunktet
Fysikøvelse Erik Vestergaard www.matematikfysik.dk Radioaktive henfald Formål Formålet i denne øvelse er at eftervise henfaldsloven A( t) = A0 e kt, hvor A 0 er den radioaktive kildes aktivitet til tidspunktet
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Andengradsligninger. Frank Nasser. 12. april 2011
 Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Andengradsligninger Frank Nasser 12. april 2011 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter (især for B- og A-niveau)
 Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
Projekt 2.9 Sumkurver som funktionsudtryk anvendt til Lorenzkurver og Ginikoefficienter En sumkurve fremkommer ifølge definitionen, ved at vi forbinder en række punkter afsat i et koordinatsystem med rette
Bedste rette linje ved mindste kvadraters metode
 1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
1/9 Bedste rette linje ved mindste kvadraters metode - fra www.borgeleo.dk Figur 1: Tre datapunkter og den bedste rette linje bestemt af A, B og C Målepunkter og bedste rette linje I ovenstående koordinatsystem
Taylors formel. Kapitel Klassiske sætninger i en dimension
 Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Kapitel 3 Taylors formel 3.1 Klassiske sætninger i en dimension Sætning 3.1 (Rolles sætning) Lad f : [a, b] R være kontinuert, og antag at f er differentiabel i det åbne interval (a, b). Hvis f (a) = f
Andengradsligninger. Frank Nasser. 11. juli 2011
 Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Andengradsligninger Frank Nasser 11. juli 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Løsninger til eksamensopgaver på A-niveau 2016
 Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Løsninger til eksamensopgaver på A-niveau 2016 24. maj 2016: Delprøven UDEN hjælpemidler Opgave 1: Da trekanterne er ensvinklede, er forholdene mellem korresponderende linjestykker i de to trekanter det
Excel regneark. I dette kapitel skal I arbejde med noget af det, Excel regneark kan bruges til. INTRO EXCEL REGNEARK
 Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
Excel regneark Et regneark er et computerprogram, der bl.a. kan regne, tegne grafer og lave diagrammer. Regnearket kan bruges i mange forskellige sammenhænge, når I arbejder med matematik. Det kan gøre
2 Erik Vestergaard www.matematikfysik.dk
 Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
Erik Vestergaard www.matematikfysik.dk Erik Vestergaard www.matematikfysik.dk 3 Lineære funktioner En vigtig type funktioner at studere er de såkaldte lineære funktioner. Vi skal udlede en række egenskaber
Mandags Chancen. En optimal spilstrategi. Erik Vestergaard
 Mandags Chancen En optimal spilstrategi Erik Vestergaard Spilleregler denne note skal vi studere en optimal spilstrategi i det spil, som i fjernsynet går under navnet Mandags Chancen. Spillets regler er
Mandags Chancen En optimal spilstrategi Erik Vestergaard Spilleregler denne note skal vi studere en optimal spilstrategi i det spil, som i fjernsynet går under navnet Mandags Chancen. Spillets regler er
Brugervejledning til Graph
 Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Graph (brugervejledning) side 1/17 Steen Toft Jørgensen Brugervejledning til Graph Graph er et gratis program, som ikke fylder meget. Downloades på: www.padowan.dk/graph/. Programmet er lavet af Ivan Johansen,
Introduktion til EXCEL med øvelser
 Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
Side 1 af 10 Introduktion til EXCEL med øvelser Du kender en almindelig regnemaskine, som kan være til stort hjælp, når man skal beregne resultater med store tal. Et regneark er en anden form for regnemaskine,
1. Opbygning af et regneark
 1. Opbygning af et regneark Et regneark er et skema. Vandrette rækker og lodrette kolonner danner celler, hvori man kan indtaste tal, tekst, datoer og formler. De indtastede tal og data kan bearbejdes
1. Opbygning af et regneark Et regneark er et skema. Vandrette rækker og lodrette kolonner danner celler, hvori man kan indtaste tal, tekst, datoer og formler. De indtastede tal og data kan bearbejdes
Betydningen af ordet differentialkvotient...2. Sekant...2
 PeterSørensen.dk Differentiation Indold Betydningen af ordet differentialkvotient... Sekant... Differentiable funktioner...3 f (x) er grafens ældning i punktet med første-koordinaten x....3 Ikke alle grafpunkter
PeterSørensen.dk Differentiation Indold Betydningen af ordet differentialkvotient... Sekant... Differentiable funktioner...3 f (x) er grafens ældning i punktet med første-koordinaten x....3 Ikke alle grafpunkter
Introduktion til den afledede funktion
 Introduktion til den afledede funktion Scenarie: Rutsjebanen Tilsigtede viden Bredere kompetencemål Nødvendige matematiske forudsætninger Tid Niveau Materialer til rådighed At give en forståelse for konceptet
Introduktion til den afledede funktion Scenarie: Rutsjebanen Tilsigtede viden Bredere kompetencemål Nødvendige matematiske forudsætninger Tid Niveau Materialer til rådighed At give en forståelse for konceptet
Jævn cirkelbevægelse udført med udstyr fra Vernier
 Fysikøvelse - Erik Vestergaard www.matematikfysik.dk 1 Jævn cirkelbevægelse udført med udstyr fra Vernier Formål Formålet med denne øvelse er at eftervise følgende formel for centripetalkraften på et legeme,
Fysikøvelse - Erik Vestergaard www.matematikfysik.dk 1 Jævn cirkelbevægelse udført med udstyr fra Vernier Formål Formålet med denne øvelse er at eftervise følgende formel for centripetalkraften på et legeme,
Opvarmningsopgaver. Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3. Forkort brøken. Gang parentesen ud: (x 0 + x) 3
 eks. Intro til differentialregning side 1 Opvarmningsopgaver 10. november 2012 12:58 Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3 Gang parentesen ud: Forkort brøken (x
eks. Intro til differentialregning side 1 Opvarmningsopgaver 10. november 2012 12:58 Gang parentesen ud: Forkort brøken: Gang parentesen ud: (1.5 + x) 2 (1 + x) 3 Gang parentesen ud: Forkort brøken (x
Analyse af måledata II
 Analyse af måledata II Usikkerhedsberegning og grafisk repræsentation af måleusikkerhed Af Michael Brix Pedersen, Birkerød Gymnasium Forfatteren gennemgår grundlæggende begreber om måleusikkerhed på fysiske
Analyse af måledata II Usikkerhedsberegning og grafisk repræsentation af måleusikkerhed Af Michael Brix Pedersen, Birkerød Gymnasium Forfatteren gennemgår grundlæggende begreber om måleusikkerhed på fysiske
MATEMATIK A-NIVEAU-Net Forberedelsesmateriale
 STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
STUDENTEREKSAMEN SOMMERTERMIN 13 MATEMATIK A-NIVEAU-Net Forberedelsesmateriale 6 timer med vejledning Forberedelsesmateriale til de skriftlige prøver sommertermin 13 st131-matn/a-6513 Forberedelsesmateriale
Mike Vandal Auerbach. Differentialregning (2) (1)
 Mike Vandal Auerbach Differentialregning f () www.mathematicus.dk Differentialregning. udgave, 208 Disse noter er skrevet til matematikundervisningen på stx A- og B-niveau efter gymnasiereformen 207. Noterne
Mike Vandal Auerbach Differentialregning f () www.mathematicus.dk Differentialregning. udgave, 208 Disse noter er skrevet til matematikundervisningen på stx A- og B-niveau efter gymnasiereformen 207. Noterne
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Om at finde bedste rette linie med Excel
 Om at finde bedste rette linie med Excel Det er en vigtig og interessant opgave at beskrive fænomener i naturen eller i samfundet matematisk. Dels for at få en forståelse af sammenhængende indenfor det
Om at finde bedste rette linie med Excel Det er en vigtig og interessant opgave at beskrive fænomener i naturen eller i samfundet matematisk. Dels for at få en forståelse af sammenhængende indenfor det
Integralregning Infinitesimalregning
 Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Udgave 2.1 Integralregning Infinitesimalregning Noterne gennemgår begreberne integral og stamfunktion, og anskuer dette som et redskab til bestemmelse af arealer under funktioner. Noterne er supplement
Matematik A. Studentereksamen. Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet
 Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Matematik A Studentereksamen Forberedelsesmateriale til de digitale eksamensopgaver med adgang til internettet st131-matn/a-6513 Mandag den 6 maj 13 Forberedelsesmateriale til st A Net MATEMATIK Der skal
Differentialkvotient af cosinus og sinus
 Differentialkvotient af cosinus og sinus Overgangsformler cos( + p ) = cos sin( + p ) = sin cos( -) = cos sin( -) = -sin cos( p - ) = - cos sin( p - ) = sin cos( p + ) = -cos sin( p + ) = -sin (bevises
Differentialkvotient af cosinus og sinus Overgangsformler cos( + p ) = cos sin( + p ) = sin cos( -) = cos sin( -) = -sin cos( p - ) = - cos sin( p - ) = sin cos( p + ) = -cos sin( p + ) = -sin (bevises
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk
 Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
Numeriske metoder - til løsning af differentialligninger - fra borgeleo.dk Eksakte løsninger: fuldstændig løsning og partikulær løsning Mange differentialligninger kan løses eksakt. Fx kan differentialligningen
OPGAVER 1. Approksimerende polynomier. Håndregning
 OPGAVER 1 Opgaver til Uge 4 Store Dag Opgave 1 Approksimerende polynomier. Håndregning a) Find for hver af de følgende funktioner deres approksimerende polynomiumer af første og anden grad med udviklingspunkt
OPGAVER 1 Opgaver til Uge 4 Store Dag Opgave 1 Approksimerende polynomier. Håndregning a) Find for hver af de følgende funktioner deres approksimerende polynomiumer af første og anden grad med udviklingspunkt
Matematik opgave Projekt afkodning Zehra, Pernille og Remuss
 Matematik opgave Projekt afkodning Zehra, Pernille og Remuss Opgave A Sæt de overstående symboler ind i en matematisk sammenhæng der gør dem forståelige. Det kan være som en sætning eller med tal og bogstaver
Matematik opgave Projekt afkodning Zehra, Pernille og Remuss Opgave A Sæt de overstående symboler ind i en matematisk sammenhæng der gør dem forståelige. Det kan være som en sætning eller med tal og bogstaver
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
lineær regression er en metode man bruger for at finde den mindste afstand mellem bestemte punkter ved at bruge denne formel: a= n i=1 i=1
 Linær regression lineær regression er en metode man bruger for at finde den mindste afstand mellem bestemte punkter ved at bruge denne formel: a= (Xi Yi) n * Xi 2 n * x 2 x * y Figur 1. Nu vil vi løse
Linær regression lineær regression er en metode man bruger for at finde den mindste afstand mellem bestemte punkter ved at bruge denne formel: a= (Xi Yi) n * Xi 2 n * x 2 x * y Figur 1. Nu vil vi løse
Introduktion til Calc Open Office med øvelser
 Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Side 1 af 8 Introduktion til Calc Open Office med øvelser Introduktion til Calc Open Office... 2 Indtastning i celler... 2 Formler... 3 Decimaler... 4 Skrifttype... 5 Skrifteffekter... 6 Justering... 6
Disposition for kursus i Excel2007
 Disposition for kursus i Excel2007 Analyse af data (1) Demo Øvelser Målsøgning o evt. opgave 11 Scenariestyring o evt. opgave 12 Datatabel o evt. opgave 13 Evt. Graf og tendens o evt. opgave 10 Subtotaler
Disposition for kursus i Excel2007 Analyse af data (1) Demo Øvelser Målsøgning o evt. opgave 11 Scenariestyring o evt. opgave 12 Datatabel o evt. opgave 13 Evt. Graf og tendens o evt. opgave 10 Subtotaler
APPENDIX A INTRODUKTION TIL DERIVE
 APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
APPENDIX A INTRODUKTION TIL DERIVE z x y z=exp( x^2 0.5y^2) CAS er en fællesbetegnelse for matematikprogrammer, som foruden numeriske beregninger også kan regne med symboler og formler. Det betyder: Computer
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Matematisk modellering og numeriske metoder. Lektion 13
 Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 3. november 206 Numerisk metode til Laplace- og Poisson-ligningerne. Finite difference-formulering af problemet I det følgende
Matematisk modellering og numeriske metoder Lektion 3 Morten Grud Rasmussen 3. november 206 Numerisk metode til Laplace- og Poisson-ligningerne. Finite difference-formulering af problemet I det følgende
Tilpas: Hurtig adgang
 Tilpas: Hurtig adgang Genveje, Se skærmtips Se tips Hold alt tasten nede. Og brug bogstaver Word Fanen Filer PDF dokument Brug skabelon Visninger Husk Luk ved fuldskærmsvisning Brug zoom skyder Marker,
Tilpas: Hurtig adgang Genveje, Se skærmtips Se tips Hold alt tasten nede. Og brug bogstaver Word Fanen Filer PDF dokument Brug skabelon Visninger Husk Luk ved fuldskærmsvisning Brug zoom skyder Marker,
Skabelon til funktionsundersøgelser
 Skabelon til funktionsundersøgelser Nedenfor en angivelse af fremgangsmåder ved funktionsundersøgelser. Ofte vil der kun blive spurgt om et udvalg af nævnte spørgsmål. Syntaksen i løsningerne vil være
Skabelon til funktionsundersøgelser Nedenfor en angivelse af fremgangsmåder ved funktionsundersøgelser. Ofte vil der kun blive spurgt om et udvalg af nævnte spørgsmål. Syntaksen i løsningerne vil være
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå
 qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå Polynomier Kort gennemgang af polynomier og deres asdfghjklæøzxcvbnmqwertyuiopåasd
qwertyuiopåasdfghjklæøzxcvbnmqw ertyuiopåasdfghjklæøzxcvbnmqwert yuiopåasdfghjklæøzxcvbnmqwertyui opåasdfghjklæøzxcvbnmqwertyuiopå Polynomier Kort gennemgang af polynomier og deres asdfghjklæøzxcvbnmqwertyuiopåasd
MODELSÆT 2; MATEMATIK TIL LÆREREKSAMEN
 MODELSÆT ; MATEMATIK TIL LÆREREKSAMEN Forberedende materiale Den individuelle skriftlige røve i matematik vil tage udgangsunkt i følgende materiale:. En diskette med to regnearks-filer og en MathCad-fil..
MODELSÆT ; MATEMATIK TIL LÆREREKSAMEN Forberedende materiale Den individuelle skriftlige røve i matematik vil tage udgangsunkt i følgende materiale:. En diskette med to regnearks-filer og en MathCad-fil..
Residualer i grundforløbet
 Erik Vestergaard www.matematikfysik.dk 1 Residualer i grundforløbet I dette lille tillæg til grundforløbet, skal vi kigge på begreberne residualer, residualplot samt residualspredning. Vi vil se, hvad
Erik Vestergaard www.matematikfysik.dk 1 Residualer i grundforløbet I dette lille tillæg til grundforløbet, skal vi kigge på begreberne residualer, residualplot samt residualspredning. Vi vil se, hvad
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Newtons afkølingslov
 Newtons afkølingslov miniprojekt i emnet differentialligninger Teoretisk del Vi skal studere, hvordan temperaturen i en kop kaffe aftager med tiden. Lad T ( t ) betegne temperaturen i kaffen til tiden
Newtons afkølingslov miniprojekt i emnet differentialligninger Teoretisk del Vi skal studere, hvordan temperaturen i en kop kaffe aftager med tiden. Lad T ( t ) betegne temperaturen i kaffen til tiden
Projekt 3.5 faktorisering af polynomier
 Projekt 3.5 faktorisering af polynomier Hvilke hele tal går op i tallet 60? Det kan vi få svar på ved at skrive 60 som et produkt af sine primtal: 60 3 5 Divisorerne i 60 er lige præcis de tal, der kan
Projekt 3.5 faktorisering af polynomier Hvilke hele tal går op i tallet 60? Det kan vi få svar på ved at skrive 60 som et produkt af sine primtal: 60 3 5 Divisorerne i 60 er lige præcis de tal, der kan
Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen
 Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen Microsoft Excel har en del standard anvendelsesmuligheder i forhold til den beskrivende statistik og statistisk
Bilag til Statistik i løb : Statistik og Microsoft Excel tastevejledning / af Lars Bo Kristensen Microsoft Excel har en del standard anvendelsesmuligheder i forhold til den beskrivende statistik og statistisk
Mat H /05 Note 2 10/11-04 Gerd Grubb
 Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Mat H 1 2004/05 Note 2 10/11-04 Gerd Grubb Nødvendige og tilstrækkelige betingelser for ekstremum, konkave og konvekse funktioner. Fremstillingen i Kapitel 13.1 2 af Sydsæters bog [MA1] suppleres her med
Funktion af flere variable
 Funktion af flere variable Preben Alsolm 24. april 2008 1 Funktion af flere variable 1.1 Differentiabilitet for funktion af én variabel Differentiabilitet for funktion af én variabel f kaldes differentiabel
Funktion af flere variable Preben Alsolm 24. april 2008 1 Funktion af flere variable 1.1 Differentiabilitet for funktion af én variabel Differentiabilitet for funktion af én variabel f kaldes differentiabel
Grafværktøjer til GeoMeter Grafværktøjer Hjælp Grafværktøjer.gsp Grafværktøjer
 Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Grafværktøjer til GeoMeter Bjørn Felsager, Haslev Gymnasium & HF, 2003 Når man installerer GeoMeter på sin maskine følger der en lang række specialværktøjer med. Men det er også muligt at skræddersy sine
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Regneark Excel fortsat
 Regneark Excel fortsat Indhold SÅDAN TEGNES GRAFER I REGNEARK EXCEL... 1 i Excel 97-2003... 1 I Excel 2007... 1 ØVELSE... 2 I Excel 97-2003:... 2 I Excel 2007... 3 OM E-OPGAVER 12A... 4 Sådan tegnes grafer
Regneark Excel fortsat Indhold SÅDAN TEGNES GRAFER I REGNEARK EXCEL... 1 i Excel 97-2003... 1 I Excel 2007... 1 ØVELSE... 2 I Excel 97-2003:... 2 I Excel 2007... 3 OM E-OPGAVER 12A... 4 Sådan tegnes grafer
Matematik og IT Anton Vilhelm Wiinstedt Clausen 3.b Studieretningsprojekt Numeriske metoder Frederiksberg Tekniske gymnasium 13/12 2010
 Indholdsfortegnelse Abstract...2 Indledning...3 Konvergens...3 Konvergenskriterier...3 Konvergensorden...3 Fejlestimater...3 Stopkriterier...4 Taylor's Theorem...4 Numeriske metoder...4 Newtonsmetode...4
Indholdsfortegnelse Abstract...2 Indledning...3 Konvergens...3 Konvergenskriterier...3 Konvergensorden...3 Fejlestimater...3 Stopkriterier...4 Taylor's Theorem...4 Numeriske metoder...4 Newtonsmetode...4
1 monotoni & funktionsanalyse
 1 monotoni & funktionsanalyse I dag har vi grafregnere (TI89+) og programmer på computer (ex.vis Derive og Graph), hvorfor det ikke er så svært at se hvordan grafen for en matematisk funktion opfører sig
1 monotoni & funktionsanalyse I dag har vi grafregnere (TI89+) og programmer på computer (ex.vis Derive og Graph), hvorfor det ikke er så svært at se hvordan grafen for en matematisk funktion opfører sig
Lineære sammenhænge, residualplot og regression
 Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Lineære sammenhænge, residualplot og regression Opgave 1: Er der en bagvedliggende lineær sammenhæng? I mange sammenhænge indsamler man data som man ønsker at undersøge og afdække eventuelle sammenhænge
Tak for kaffe! 17-10-2004 Tak for kaffe! Side 1 af 16
 Tak for kaffe! Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004 Tak for kaffe! Side 1 af 16 Tak
Tak for kaffe! Jette Rygaard Poulsen, Frederikshavn Gymnasium og HF-kursus Hans Vestergaard, Frederikshavn Gymnasium og HF-kursus Søren Lundbye-Christensen, AAU 17-10-2004 Tak for kaffe! Side 1 af 16 Tak
π can never be expressed in numbers. William Jones og John Machins algoritme til beregning af π
 can never be expressed in numbers. William Jones og John Machins algoritme til beregning af. Oprindelsen til symbolet Første gang vi møder symbolet som betegnelse for forholdet mellem en cirkels omkreds
can never be expressed in numbers. William Jones og John Machins algoritme til beregning af. Oprindelsen til symbolet Første gang vi møder symbolet som betegnelse for forholdet mellem en cirkels omkreds
Åbn Paint, som er et lille tegne- og billedbehandlingsprogram der findes under Programmer i mappen Tilbehør. Åbn også Word.
 75 Paint & Print Screen (Skærmbillede med beskæring) Åbn Paint, som er et lille tegne- og billedbehandlingsprogram der findes under Programmer i mappen Tilbehør. Åbn også Word. 1. Minimer straks begge
75 Paint & Print Screen (Skærmbillede med beskæring) Åbn Paint, som er et lille tegne- og billedbehandlingsprogram der findes under Programmer i mappen Tilbehør. Åbn også Word. 1. Minimer straks begge
Partielle afledede og retningsafledede
 Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Partielle afledede og retningsafledede 1 Partielle afledede, definitioner og notationer Bertragt en funktion af to reelle variable f : D R, hvor D R 2 er et åbent område Med benyttelse af tilvækstfunktionen
Indhold Forelæsning Dat-D1: Regneark Matematik og databehandling 2012
 Indhold Forelæsning Dat-D1: Regneark Matematik og databehandling 2012 Henrik L. Pedersen Institut for Matematiske Fag henrikp@life.ku.dk 1 Forberedelsesopgaverne Dat-D-1 og Dat-D-2 2 Regnearks grundprincipper
Indhold Forelæsning Dat-D1: Regneark Matematik og databehandling 2012 Henrik L. Pedersen Institut for Matematiske Fag henrikp@life.ku.dk 1 Forberedelsesopgaverne Dat-D-1 og Dat-D-2 2 Regnearks grundprincipper
Projekt 4.6 Løsning af differentialligninger ved separation af de variable
 Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Projekt 4.6 Løsning af differentialligninger ved separation af de variable Differentialligninger af tpen d hx () hvor hx ()er en kontinuert funktion, er som nævnt blot et stamfunktionsproblem. De løses
Graph brugermanual til matematik C
 Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Graph brugermanual til matematik C Forord Efterfølgende er en guide til programmet GRAPH. Programmet kan downloades gratis fra nettet og gemmes på computeren/et usb-stik. Det betyder, det også kan anvendes
Microsoft Excel - en kort introduktion. Grundlag
 Microsoft Excel - en kort introduktion Grundlag Udover menuer og knapper - i princippet som du kender det fra Words eller andre tekstbehandlingsprogrammer - er der to grundlæggende vigtige størrelser i
Microsoft Excel - en kort introduktion Grundlag Udover menuer og knapper - i princippet som du kender det fra Words eller andre tekstbehandlingsprogrammer - er der to grundlæggende vigtige størrelser i
Elementær Matematik. Funktioner og deres grafer
 Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Elementær Matematik Funktioner og deres grafer Ole Witt-Hansen 0 Indhold. Funktioner.... Grafen for en funktion...3. grafers skæring med koordinat akser...4. To grafers skæringspunkter...4 3. Egenskaber
Seriediagrammer - Guide til konstruktion i LibreOffice Calc
 Seriediagrammer - Guide til konstruktion i LibreOffice Calc På forbedringsvejlederuddannelsen anvender vi seriediagrammer til at skelne mellem tilfældig og ikketilfældig variation. Med et seriediagram
Seriediagrammer - Guide til konstruktion i LibreOffice Calc På forbedringsvejlederuddannelsen anvender vi seriediagrammer til at skelne mellem tilfældig og ikketilfældig variation. Med et seriediagram
Indholdsfortegnelse. Regneark for matematiklærere
 Indholdsfortegnelse Forord... 3 Diskettens indhold... 4 Grafer i koordinatsystemet... 5 Brug af guiden diagram... 5 Indret regnearket fornuftigt... 9 Regneark hentet på Internettet... 15 Læsevenlige tal
Indholdsfortegnelse Forord... 3 Diskettens indhold... 4 Grafer i koordinatsystemet... 5 Brug af guiden diagram... 5 Indret regnearket fornuftigt... 9 Regneark hentet på Internettet... 15 Læsevenlige tal
