2 Lektion Opgave C Opgave Opgave Opgave Opgave a b...
|
|
|
- Birgit Lund
- 7 år siden
- Visninger:
Transkript
1
2 .
3 Indhold 1 Lektion Opgave A Opgave a b Opgave Opgave Opgave Bonus Opgave Bonus Lektion 5.1 Opgave C Opgave Opgave Opgave Opgave a b Lektion Opgave D D D Bestem p i r- og p-rum Lektion Opgave Bonus Opgave E E E E Opgave a b I
4 II INDHOLD 5 Lektion Opgave F F F F F Lektion Opgave H Lektion Opgave I Opgave J Lektion Opgave O Opgave O Opgave P Opgave Opgave L Lektion Opgave 7.3c Opgave Q Opgave R Lektion Opgave regning nr Opgave regning nr Opgave S Lektion Opgave U Opgave V Opgave W Lektion Opgave X Opgave a b c Opgave Bonus
5 INDHOLD III 13 Lektion Opgave Y Opgave Opgave 10.3a Lektion Opgave Lektion Opgave Z Eksamens spørgsmål Opgave Partikel-bølge-dualiteten Bølgefunktioner, bølgepakker Schrödingerligningen Opgave Position og bevægelsesmængde Forventningsværdier og usikkerheder Heisenbergs usikkerhedsrelation Opgave Hamiltonoperatoren Den tidsuafhængige Schrödingerligning Overlejringer af egentilstande for Hamiltonoperatoren Opgave Kvantebrønde Potentialbarrierer Tunneleffekten Opgave Den harmoniske oscillator Vibrationer i to-atomige molekyler Opgave Operatorrepræsentanter og disses egenskaber, fuldstændige sæt. 85. Samtidigt målbare observable, kommutatorrelationer Opgave Bevægelsesmængdemoment Egentilstande for ˆL og ˆL z, radiale bølgefunktioner og sfærisk harmoniske Spin
6 IV INDHOLD 4 Opgave Centralpotentialer, herunder reduceret masse Den radiale Schrödingerligning Brintatomet, kvantetal Opgave Uskelnelige partikler, herunder udvekslingssymmetri Bosoner og fermioner Opgave Atomer og molekyler, herunder centralfelttilnærmelsen Elektronkonfiguration og det periodiske system Bindingslængden i en H + -ion A Definitioner og andre nice ting 107 A.1 Plank s konstant - h A. Elektronvolt - ev A.3 Rydberg - Ry A.4 Bølgefunktionen / Egenfunktionen - Ψ A.5 Egentilstand A.6 Den generelle Schrödingerligning A.7 Delta funktioner - δ A.7.1 Dirac delta funktion A.7. Kronecker delta funktion A.8 Hamilton operator - Ĥ A.9 Nulpunkts energi A.10 Hermitisk opperator - O A.11 Paritet A.1 Dispersions relationen B Maple for opgave Z 111
7 Kapitel 1 Lektion Opgave A Vis, at middelværdien for sandsynlighedsfordelingen P (E) = 1 k B T e E k B T er givet ved: < E >= EP (E)dE = k 0 B T. Det eneste man blot skal gøre er at sætte P (E) ind og løse udtrykket. < E >= 0 = 1 k B T = 1 k B T = 1 k B T =k B T E 1 k B T e E k B T de (1.1) 0 Ee E k B T de [ Ek B T e E k B T ] (k B T ) e E k B T 0 ( ( (kb T ) ) ) Man har nu bevist at start argumentet gælder. 1. Opgave 1. En elektron kan exciteres fra en skal ved at tilføre et atom en energi, som fx lys a Hvis der findes en minimums løsrivelsesenergi, energien af en elektron er givet ved: E = hν, ses det, da E og ν er proportiunelle, at følgende glæder: E min = hν min. 1
8 KAPITEL 1. LEKTION b For at løsrive en elektron fra magnesium (Mg) kræves at følgende gælder: E min 3, 68[eV ], hvor E min er den energi man tilfører atomet. Hvis man anvender det man fandt i forrige delopgave får man: E min = hν min ν min = E min h Man kender h fra afsnit A.1 og E min er givet ved den minimums energi man har fået givet ganget med værdien for en elektronvolt. Dette kan nu anvendes til at finde den minimale løsrivelsesfrekvenz, ν min. ν min = 3, 68 1, [J] 6, [Js] = 8, [Hz] (1.) Dette betyder at den minimale værdi for løsrivelsesfrekvenz af Mg er: ν 8, [Hz]. 1.3 Opgave 1.5 En elektron har en bane rundt omkring en atom kerne, dette kan betrages med klassisk mekanisk, hvis det angulere moment, L, er meget større en h. Vis at dette tilfælde er opfyldt ar hvis radiusen for banen er meget større end Bohr radiusen, altså at følgende er opfyldt: r a 0 L h a 0 = 4πɛ 0 e h m e Dette kan man gøre ved at omskrive på det angulere moment (L = r m v = rm e v): L(r; v) v(r) L(r) For at finde hastigheden som funktion af radiusen r kan man benytte sig af den resulterende kraft og Coulomb kraften: m e a = m e v r = e 4πɛ 0 r Dette kan nu omskrives til at finde hastigheden v: v e e = v = 4πɛ 0 rm e 4πɛ 0 rm e Dette udtryk kan nu indsættes i det man kender om det angulere moment: e L = rm e e = rm e 4πɛ 0 rm e 4πɛ 0
9 1.4. OPGAVE Dette er det generelle tilfælde for det angulere moment, hvis man nu antager at r = a 0 og indsætter finder man: ( ) e 4πɛ 0 h e L = m e m e = h 4πɛ 0 Hvis man nu antager at r a 0 må man også antage at L h, da når r = a 0 gælder L = h. 1.4 Opgave 1.9 Forklar hvorfor elektroner som sendes ind imod en plade nikkel bliver kastet tilbage med en vinkel på 50. Man kan anvende formel (1.7) på side 5 i KM bogen. Denne er formel er en afledning af Louis de Broglie s formel: λ = h me Hvis man nu indsætter det man kender får man følgende, E = νh. λ = 6, [Js] = 0, 168[nm] (9, [kg]) (54 1, [J]) Nu da man har bølgelængden, λ, kan man udregne vinklen, θ. ( ) nλ d sin(θ) = nλ θ = arcsin d Dette giver: θ = arcsin ( ) n 0,168[nm] 0,15[nm] 1.5 Opgave Bonus 1 Vis at følgende gælder: lim ν 0 n = 1, θ =, 85 n =, θ = 50, 96 n = 3, θ =ikke defineret hν e hν k B T 1 = k B T Man kan løse problemet for dette udtryk ved at udvikle over og under brøken omkring ν 0 = 0, løsninger findes ved at Taylor udvikle hhv. over og under brøken: hν = hν ! ν (hν)(ν ν 0) = h (hν)(ν 0) = hν 1! ν ) + 1 ) (e hν k B T 1 (ν ν 0 ) = h 1! ν k B T e hν k B T ν = e hν k B T 1 = (e hν k B T 1 hν k B T
10 4 KAPITEL 1. LEKTION 1 Disse resultater kan nu indsættes for at verificerer resultatet: lim ν 0 hν e hν k B T 1 = lim ν 0 hν lim ν 0 Man kan se at resultatet stemmer! 1.6 Opgave Bonus Vis at følgende gælder: lim ν hν hν k B T e hν k B T 1 = hν hν k B T = 0 = k B T Den anden formel er er ligetil, hvis man indsætter på ν s plads og regner får man at nævneren går hurtigere imod uendelig end tælleren og derved går hele brøken imod nul. Den første brøk er dog lidt mere besværlig, her skal man Taylor række udvikle for at komme frem til det resultat der søges:
11 Kapitel Lektion.1 Opgave C Vis, at Schrödingerligningen opfylder linearitetsbetingelsen. Schrödingerligningen er beskrevet i afsnit A.6, og er givet ved: i h Ψ t = h m Ψ. Det man gr er at antage at aψ 1 ( r, t) og bψ ( r, t) er lsninger. Disse indsttes nu i Schrödingerligningen og udregnes. aψ 1 ( r, t) : ai h Ψ 1 t = a h m Ψ 1 bψ ( r, t) : bi h Ψ = b h t m Ψ Hvis man lgger disse to lsninger sammen fr man: ai h Ψ 1 t + bi h Ψ t = a h m Ψ 1 b h m Ψ (.1) Det man skal vise er at dette resultat fundet i formel.1 er korrekt, det kan verificeres ved at gre flgende: Ψ = aψ 1 + bψ ; i h (aψ 1 + bψ ) t = h m (aψ 1 + bψ ) ai h Ψ 1 + bi h Ψ = a h t t m Ψ 1 b h m Ψ (.) Man kan se at formel.1 er lig formel... Opgave.1 Bølger i vandet har en sinus agtig bevægelse, ω er givet ved: T k ω = 3 ρ 5
12 6 KAPITEL. LEKTION Hvor T er overflade spændingen, ρ er vands densitet og k er bølgenummeret. Find et udtryk for fase hastigheden for en sinus bølge af vand (1) og find et udtryk for gruppe hastighed for en gruppe bølger med bølgenummer tæt på k (). (1) Fase hastighed er givet ved ligningen på side 6 i KM bogen: v fase = ω k = g k Dette kan bruges til at finde hastigheden for os: T k 3 ρ v fase = = k T k k k ρ = T k ρ (.3) () Gruppe hastighed er givet ved ligningen på side 6 i KM bogen: v gruppe = dω dk = 1 g k Vi har flere bølger hvor bølgetalle ligger meget tæt på hinanden. Vi benytter os af fase udtrykke fra den generelle Bølgefunktion, som udledes til følgende udtryk da der er konstruktiv interference. k x ωt = (k + dk) x (ω + dω)t = kx + dkx ωt dωt Forkortes der ud får man følgende udtryk som man man bruge til at finde gruppe hastigheden: 0 = dkx dωt dωt = dkx dωt dk = x dω dk = x t = v gruppe nu indsætter man det man kender og finder resultatet: ( ) T k d 3 ρ v gruppe = dk = 1 T k 3 ρ 3k T ρ = 3k T T k 3 ρ = 3T ρ T k = 3 ρ T k (.4).3 Opgave. Følgende er givet på forhånd: Ψ(x, t) = k+ k k k A cos(k x ω t)dk
13 .3. OPGAVE. 7 ω = ck Dette bruges ved at man indsætter det andet argument i det første og udregner dette: Ψ(x, t) = k+ k k k A cos(k x ck t)dk A antages at være konstant og sættes derfor udenfor integralet og k sættes udenfor en ( ) i cosinusen. Dette udregnes: Ψ(x, t) = A [ sin(k (x ct)) Ψ(x, t) =A x ct ] k+ k k+ k k k k k cos(k (x ct))dk (.5) = A (sin((k + k)(x ct)) sin((k k)(x ct))) x ct = A (sin(k(x ct) + k(x ct)) sin(k(x ct) k(x ct))) x ct Nu anvendes en trigonometrisk additions formel for at komme videre: (sin(u± v) = sin(u) cos(v) ± cos(u) sin(v), hvor u = k(x ct) og v = k(x ct)) Ψ(x, t) = A ((sin(k(x ct)) cos( k(x ct)) + cos(k(x ct)) sin( k(x ct))) x ct (.6) (sin(k(x ct)) cos( k(x ct)) cos(k(x ct)) sin( k(x ct)))) = A cos(k(x ct)) sin( k(x ct)) x ct Man kan se at man bevæger sig i +x retningen da x ct skal være konstant for at man holder sig på samme punkt på bølgen, så hvis tiden t siger skal x ligelides stige. Forlænger man hele dette udtryk med k får man det udtryk som der står man skal frem til: k sin( k(x ct)) S(x ct) = A k k(x ct) (.7) Plotter man denne funktion får man: Figur.1 viser en sinc funktion, hvor afstanden hen til første 0 gennemgang svare til hvor lokaliseret den er, dvs. des større k des større lokalisering.
14 8 KAPITEL. LEKTION Figur.1: Dette er en sinc funktion sin(x). Afstanden hen til første 0 gennemgang x svare til hvor lokaliseret den er, dvs. des større k des større lokalisering..4 Opgave.3 Schr øligningen for fri partikler er givet ved følgende da potentialet er 0: i h Ψ t = h m Ψ Man indsætte de to Bølgeligningen man har og udregner ligningen og det man kommer frem til er at der er en imaginær del på den ene side og ikke på den anden, hvilket vil sige at disse Bølgefunktioner ikke opfylder Schröligningen..5 Opgave a Vis at Ψ(x, t) = Ae i(kx ωt) Ae i(kx+ωt) er en lsning til Schrödingerligningen. Det man gr for at lse dette problem er at indstte den opgivede lsning for Ψ i Schrödingerligningen og lse denne. Husk at hω = h k m ; i h ( Ae i(kx ωt) Ae i(kx+ωt)) t = h m ( Ae i(kx ωt) Ae i(kx+ωt)) (.8) i h (A( iω)e i(kx ωt) A( iω)e i(kx+ωt)) = (A(ik) h e i(kx ωt) A( ik) e i(kx+ωt)) m (e i(kx ωt) e i(kx+ωt)) = h k i ha( iω) haω ( e i(kx ωt) e i(kx+ωt)) = hωa Man kan se at ligningen glder! ( m A ( 1)e i(kx ωt) ( 1) e i(kx+ωt)) (e i(kx ωt) e i(kx+ωt))
15 .5. OPGAVE b Vis at Ψ(x, t) = Ae i(kx ωt) Ae i(kx+ωt) kan skrives som Ψ(x, t) = Ai sin(kx)e iωt. Det man gr er at benytte sig af de generelle regneregler for e funktioner. Ae i(kx ωt) Ae i(kx+ωt) = A ( e ikx e iωt e ikx e iωt) (.9) = Ae iωt ( e ikx e ikx) = Ae iωt i sin(kx) = Ai sin(kx)e iωt Man benytter sig af denne regneregel: eiγ e iγ i = sin(γ) e iγ e iγ = i sin(γ). Resultatet stemmer fint da det er stende monokromatisk blge som vi har med at gre. Det trix som vi anvender, kan bruges da de har samme frekvens.
16 10 KAPITEL. LEKTION
17 Kapitel 3 Lektion Opgave D D1 Find bølgefunktionen Ψ(x, t) for en kvantepartikel i en 1D kvantebrønd kendetegnet ved potentialet U(x). Figur 3.1: Her ses en skitsering af en kvantebrønd, hvor potentialet udenfor brønden er uendeligt og bølgefunktionen udenfor er nul, hvorimod inden i brønden er begge defineret. Først opstilles Schrödingerlingingen: i h Ψ t = h Ψ + U(x)Ψ(x, t) (3.1) m x Hvor, når man er udenfor kvantebrønden, Ψ(x, t) = 0 da der ingen bølge er. Man tager nu og gætter en løsning til bølgeligningen: Ψ(x, t) = Ae i(kx ωt) + Be i(kx+ωt) Nu kan gættet for Ψ(x, t) indsættes i Schrödingerlingingen, formel 3.1, for 11
18 1 KAPITEL 3. LEKTION 3 at finde en løsning til denne. i h ( iωae i(kx ωt) iωbe i(kx+ωt)) ( = h k Ae i(kx ωt) k Be i(kx+ωt)) + 0 m (3.) hω (Ae i(kx ωt) + Be i(kx+ωt)) = h k (Ae i(kx ωt) + Be i(kx+ωt)) m ω(k) = hk m Nu kan man finde A og B ud fra de grænse betingelser man kender og det man ved om bølgefunktionen udenfor kvantebrønden, altså kan man finde A og B ud fra: Ψ(0, t) = 0 og Ψ(L, t) = 0. Ψ(0, t) = 0 = Ae iωt + Be iωt A + B = 0 A = B Ψ(L, t) = 0 = Ae i(kl ωt) + Be i(kl+ωt) Ud fra det man kom frem til før ved man at A = B: A(e i(kl ωt) e i(kl+ωt) ) = 0 (3.3) L = nπ k e i(kl ωt) = e i(kl+ωt) kl ωt = kl ωt + nπ kl = nπ k n = nπ L L = nλ Da man nu kender en funktion for k n kan dette indsættes i dispationsrelationen: ω n (k n ) = hk m = hn π ml Det man er kommet frem til som bølgefunktionen, kan dette omskrives til noget lettere? Ja, hvis man anvender Euler s formel (sin(γ) = eiγ e iγ i )! ( Ψ(x, t) = A e i(kl ωt) e i(kl+ωt)) (3.4) ( e ikx e iωt e ikx e iωt ) = A i = A (e iωt eikx e ikx ) i = Ae iωt sin(kx) = Ae iωt sin(kx)i
19 3.. BESTEM P I R- OG P -RUM 13 Dette resultat kan nu indsættes i et integrale fra 0 til L, som skal give 1 inden i kvantebrønden. L 0 L x=0 4 A L 4 A [ x x=0 4 A ( L Ae iωt sin(kx)i dx = 1 (3.5) Ae iωt sin(kx)i A e iωt sin(kx)( i)dx = 1 sin (kx)dx = 1 cos(kx) sin(kx) k cos(kl) sin(kl) k ] L = 1 x=0 ) = 1 Der er en trigonomitri formel der siger cos(x) sin(x) = sin(x), og i og med at sin til et helt antal π er 0 udgår dette af ligningerne, det er dog skrevet med af notationsmæssige årsager første gang. ( L 4 A sin(kl) ) ( ) kl = 1 4 A = 1 4k 4k 4 A = 4k 1 kl A = L A = 1 1 i L Nu kan man udtrykke bølgefunktionen fra formel 3.4 ved hjælp af A. Først den harmoniske og dernæst den superponerede: ( nπx ) Ψ n (x, t) = L sin e iωnt (3.6) L Ψ(x, t) = a ( nπx L sin L ) ( nπx ) e iωnt + b L sin e iωnt (3.7) L Det superponerede resultat stemmer også fint, da hvis man kommer flere stående bølger ned i brønden, som svinger med den samme n så bliver bølgerne blot større! 3.1. D Skitser sandsynlighedstætheden Ψ 5 (x, t), altså er n = 5. Se figur Bestem p i r- og p-rum Matematisk er ˆ p i r-rummet givet ved: ˆ p = h i ˆp = h ) ( h i i = h ( ) = h (3.8)
20 14 KAPITEL 3. LEKTION 3 Figur 3.: Som antallet af n antyder er der fem toppe. Som blot skal fordeles over længden L. ˆp skal ikke have en vektor streg da det er en skalar. Matematisk er ˆ p i p-rummet givet ved: ˆ p = p ˆp = p (3.9)
21 Kapitel 4 Lektion Opgave Bonus 4.1 Løs egenværdiproblemet for operatoren d dx. Man starter med egenværdiproblemet for systemet: d dx φ k(x) = cφ k (x) Dette gælder da man kan benytte disse standart regne regler: ˆx = x og = c. Løser man får man følgende: ˆ x 4. Opgave E 4..1 E1 φ k (x) = Ae cx (4.1) Find de tilladte energiniveauer for en kvantepartikel i en 1D kvantebrønd kendetegnet ved potentialet V (x) = { 0 for 0 x L. for ellers Man starter med at opstille den fuldstændige løsning for Schrödingerligning jf. vores specifikke problem: Ψ(x, t) = n c n L sin(k nx)e iωnt Denne ligning kan deles op i tre forskellige funktioner, startende med en egentilstand som kan deles op i en egenfunktion og et tidsled: Ψ n (x, t) = L sin(k nx)e i En h t Bliver til: φ n (x) = ( nπx ) L sin L 15
22 16 KAPITEL 4. LEKTION 4 T (t) = e En i h t Man ved fra opgave D, afsnit 3.1, af følgende gælder: ω n = n π h ml, k n = nπ L og E n = hω n. Nu benytter man egenværdiproblemet på egenfunktionen, φ n, hørende til egenværdien, E n. Man husker Hamilton operatoren afsnit A.8: ( h L m h m ( nπx L ) x ( sin ) ( sin Ĥφ n = E n φ n (4.) ( nπx )) ( nπx ) = E n L L sin L ( nπx )) ( nπx ) = E n sin L L E n = h n π ml, n Z 4.. E Hvordan kan man alene ud fra graferne for φ m (x) og φ n (x) afgøre, hvilken af de tilhørende energiniveauer E m og E n, der er størst? Energien kan vurderes på antallet at 0-gennemgange for bølgefunktionen. Antallet af 0-gennemgange afhænger af vinkelfrekvenzen af bølgefunktionen, i vores tilfælde er vinkelfrekvenzen proportional med n, dermed jo større n des større vinkelfrekvenz des større energi! Første afledet af en funktion er tangenten. Anden afledt af en funktion er krumningen E3 Hvad bliver monstro de harmoniske løsninger Ψ nx,n y,n z ( r, t) med tilhørende energiniveauer E nx,n y,n z for en 3D kvantebrønd med V (x) = { 0 for 0 x L x og 0 x L y og 0 x L z for ellers Man starter med at opstille Hamilton operatoren og lader denne virke på den 3D egenfunktion. Den 3D egenfunktion er: φ nx,n y,n z (x, y, z) = L x L y L z sin ( nx πx L x ) sin ( ny πy L y ) ( ) nz πz sin L z
23 4.3. OPGAVE ( n Anvender man Hamilton operatoren på denne funktion får man (γ = sin xπx for at gøre notationen overskuelig): L x ) sin Ĥφ nx,n y,n z (x, y, z) = E nxn yn z φ nx,n y,n z (x, y, z) (4.3) ( ( ) ( ) ( ) Ĥφ nx,n y,n z (x, y, z) = h 8 nx π ny π nz π γ γ γ) m L x L y L z L x L y L z 8 E nxn yn z φ nx,n y,n z (x, y, z) = E nxn yn z γ L x L y L z ( ( E nxn yn z = h π ) ( ) ( ) ) nx ny nz + + m L x L y L z ( ) ( nyπy n L y sin zπz L z ), 4.3 Opgave 4.6 To stadier for en partikel med tilhørende energier E 1 og E er repræsenteret ved følgende normaliserede orthogonal løsninger til Schrödingerligningen: Ψ 1 (x, t) = φ 1 (x)e i E 1 h t Ψ (x, t) = φ (x)e i E 1 h t (4.4) (4.5) a Lav en liner superposition af de to bølgefunktioner Ψ 1 (x, t) og Ψ (x, t), som repræsenterer det stadie hvor den forventede energi er < E 1 >= 1 4 E E. Man starter med at opstille den linere superpositions ligning: Ψ super = Aφ 1 (x)e i E 1 h t + Bφ (x)e i E 1 h t Det man altså mangler er de to konstanter A og B. Disse findes ved at benytte sig af det man kender for < E 1 > og vores standart formler, < E >= n E n c n, dette viser at man skal tage absolut kvadratet af de konstanter der står foran hvert E i ligningen. Altså bliver konstanterne: A = c 1 = og B = c = 4 Dette gør at den endelige forskrift for den linere superponerede funktion bliver: 1 Ψ super = 4 φ 1(x)e i E 1 3 t h + 4 φ (x)e i E 1 h t (4.6)
24 18 KAPITEL 4. LEKTION b Find usikkerheden i energien for stadiet der er fundet i den forrige del opgave, Ψ super. Det man gør er at udregne < E >, < E > og E. < E >= 1 4 E E < E >= 1 4 E E (1 E = 4 E ) ( 1 4 E 16 E E 3 ) 16 E 1E 4 = 16 E E E 9 16 E E 1E 3 = E1 4 E + E 1E (4.7)
25 Kapitel 5 Lektion Opgave F F1 Find, på nær normering, bølgefunktionen Ψ(x, t) for en bunden kvantepartikel i en 1D kvantebrønd kendetegnet ved potentialet: V (x) = { for < x < 0 V 0 for 0 x L, V for L < x < N.B.: At kvantepartiklen er i en bunden tilstand, betyder at V 0 E 0. Læs paragraf to og tre på side 85 i Kvant bogen. Først tegnes problemet for at man kan finde ud af hvad der sker! Se figur 5.1. Man starter med at definerer egenfunktionerne i de tre områder, dette gøres ved at anvende den generelle Schrödingerligning som givet ved: Ψ(x, t) i h = h t m Ψ(x, t) + V (x)ψ(x, t) Ψ(x, t) = φ(x)e i Ē h t Man indsætter bølgefunktionen i Schrödingerligningen og udregner denne: ) (φ(x)e i Ē h t i h = h t Eφ E (x) = Ĥφ E(x) m ( φ(x)e i Ē h t) + V (x) ( φ(x)e i Ē h t) (5.1) 19
26 0 KAPITEL 5. LEKTION 5 Figur 5.1: Her ses en skitsering af opgavens kvantebrønd. Kvantebrønden er givet ved et uendeligt højt potentiale barriare ved x = 0 og et potentiale mellem 0 og V 0 ved x = L. Område 1 og 3 (pastel grøn) er udenfor og område er indeni kvantebrønden. Område 1 I område 1 på figur 5.1 er potentialet for en kvantepartikel uendeligt højt, dette medfører at egenfunktionen for en kvantepartikel vil være: Område x < 0, V (x) = φ E1 = Ψ(x, t) = 0 (5.) I område på figur 5.1, indenfor området 0 x L. Man løser egenværdiproblemet i område, for at kunne bestemme egenfunktionen i område. Dette gøres ved at anvende ligning 5.1. Den hedder V 0 da der gælder at V (x, t) = V 0. Eφ E (x) = h m φ E (x) V 0 φ E (x) (5.3) (E + V 0 )φ E (x) = h m φ E (x) Man gætter nu en løsning for funktionen φ E (x). φ E (x) = Ae Kx Dette gæt gør at man nu skal finde en funktion for K. Dette finder man ved at videre udvikle på ligning 5.3: m(e + V 0) h φ E (x) = φ E (x)
27 5.1. OPGAVE F 1 k = m(e + V 0) h (5.4) Det skal være k da man senere regner på. Nu kan man indsætte gættet for funktionen og regner K. k Ae Kx = Ae Kx (5.5) k Ae Kx = K Ae Kx k = K K = ±ik Man må lave trikket med at fjerne Ae Kx da de aldrig bliver lig nul nogle af dem! Nu kan man ved at anvende superposition finde en ligning for φ E (x). Område 3 φ E (x) = A 1 e ikx + A e ikx (5.6) I område 3 på figur 5.1, indenfor området L x. Man løser egenværdiproblemet i område 3, for at kunne bestemme egenfunktionen i område 3. Altså præcis det samme som for område, dog her skal man huske at V (x) 0 hvilket gør at E er strengt negativ. Dette gøres ved at anvende ligning 5.1. Eφ E 3 (x) = h m φ E 3 (x) 0φ E 3 (x) (5.7) (E + 0)φ E 3 (x) = h m φ E 3 (x) Man gætter nu en løsning for funktionen φ E 3 (x). φ E 3 (x) = Ae Kx Dette gæt gør at man nu skal finde en funktion for K. Dette finder man ved at videre udvikle på ligning 5.7: m(e + 0) h φ E 3 (x) = φ E 3 (x) κ = me h (5.8) Det skal være κ da man senere regner på og det skal være minus da E er strengt negativ. Nu kan man indsætte gættet for funktionen og regner K. κ Ae Kx = Ae Kx (5.9) κ Ae Kx = K Ae Kx κ = K K = ±κ
28 KAPITEL 5. LEKTION 5 Man må lave trikket med at fjerne Ae Kx da de aldrig bliver lig nul nogle af dem! Nu kan man ved at anvende superposition finde en ligning for φ E 3 (x). φ E 3 (x) = A 3 e iκx + A 4 e iκx (5.10) Foreløbig gaffelfunktion for bølgefunktionen φ: φ(x) = { 0 for < x < 0 A 1 e ikx A 1 e ikx for 0 x L A 3 e κx + A 4 e κx for L < x < Hvad er forholder mellem k og κ? Man kender ligningerne for κ og k, ligning 5.4 og ligning 5.8. Med disse ligninger kan man finde forkoldet mellem disse to, altså en funktion for den ene beskrevet med den anden. giver: mv 0 h E(k) = E(κ) h k m V 0 = h κ m κ = k + mv 0 h er en generel dybde perimeter som er beskrevet ved w. Dette indsat κ = k + w og k = κ + w (5.11) Hvad er konstanterne A 1, A, A 3 og A 4? Man finder forholdet mellem disse to konstanter ved at undersøge i grænse områderne. Først findes for grænsen x = 0, hvilket kun gør sig gældende for ligning 5.6: 0 = A E 1 + A E A E 1 = A E Dette vil medføre at ligning 5.6 kan omskrives til: φ E (x) = A 1 e ikx A 1 e ikx. Dernæst findes for grænsen x = L, denne grænse gør sig gældende for både ligning 5.6 og ligning I dette tilfælde gælder følgende: φ E = φ E 3, da disse er kontinuerte kan de omskrives til: φ E x x=l = φ E 3 x x=l (5.1) ia 1 ke ikl + ia 1 ke ikl = κa 3 e κl κa 4 e κl Nu kan man isolere sinus og cosinus. C sin(kl) = A 3 e κl + A 4 e κl kc cos(kl) = κa 3 e κl κa 4 e κl sin(kl) = A 3 C eκl + A 4 C e κl
29 5.1. OPGAVE F 3 cos(kl) = κ A 3 k C eκl κ A 4 k C e κl Nu kan κ og k indsættes for at finde konstanterne A 1, A, A 3 og A 4. Man ved fra tidligere at A = A 1 og nu indfører man at A 3 = 0 da for x må udtrykket ikke gå imod uendelig, derfor skal dette led var lige 0, derfor skal man kun finde A 1 og A 4. Endelig gaffelfunktion for bølgefunktionen φ: Hvor om der gælder: 5.1. F φ(x) = { 0 for < x < 0 A 1 e ikx A 1 e ikx for 0 x L A 4 e κx for L < x < w = k + κ og κ = k cot(kl) Se figur 5. i bogen side 87. Den siger at hvis man er imellem 0,5 og 1,5 er der en mulighed og hvis man er imellem 1,5 og,5 er der to muligheder for et resultat osv.. For at der overhovedet eksistere bundne tilstande skal w = 0.5π/L F3 Energierne er kvantiserede så længe at der er bundne tilstande, E skal altså være imellem 0 og V 0. Hvis energien er over 0 så kan den lige så vel være fri som den kan være bundet, i dette tilfælde F4 Forskellen er at i D og E er den 100 % begrænset og i dette tilfælde er den kun begrænset af en barriere. Klassisk vil partiklen bare falde ned og befinde sig i bunden af brønden, kvatemekanisk vil partiklen ikke befinde sig ET sted men smurt ud over en bølge, denne bølge kan være over alt, hvilket gør at den godt kan findes uden for barriern også selvom den er bundet af barrieren.
30 4 KAPITEL 5. LEKTION 5
31 Kapitel 6 Lektion Opgave H Løs egenværdiligningen for en 1D harmonisk oscillator: ( h d m dx + 1 ) mω x φ E (x) = Eφ E (x) (6.1) Man starter med at omskrive formel 6.1 til en tilsvarende egenværdiligning: Ĥqφ ɛ (q) = ɛφ ɛ (q) (6.) Hvor i den dimensionsløse position q x mω h og energie ɛ Ē hω E = hωɛ. Man skal finde ligningen for Ĥq, dette gør man ved at benytte sig af d kædereglen der udtrykker dx = d dq dq dx. Hvis man sammensætter de sidste to linjer får man: dq dx = mω d h som medfører at dx = d mω dq h. Disse informationer indsættes nu i en Hamilton operator funktion og denne udregnes. ( ) Ĥ q = h mω d + 1 m h dq mω q h mω = h mω m h = hω d dq + hω q = hω dq + 1 mω q h mω d ( d dq + q ) (6.3) For at kunne lave det næste skridt, behøver man først at bevise at denne regneregel gælder: (( q d ) ( q + d ) ) ) + 1 f(q) = ( d dq dq dq + q f(q) 5
32 6 KAPITEL 6. LEKTION 6 q f(q) d f(q) dq d(qf(q)) dq + q df(q) dq + f(q) = d f(q) dq Nu kan man anvende en denne differantions regneregel: d(qf(q)) dq f(q) dq dq. Anvendes denne regel, finder man at alt går ud! + q f(q) = q df(q) dq + Med denne viden kan man omskrive formel 6.1 for at komme lidt videre. Ĥ q φ E (q) = Eφ E (q) hω ) ) ( d dq + q φ ɛ (q) = hωɛφ ɛ (q) ( d dq + q φ ɛ (q) = ɛφ ɛ (q) Dette resultat kan man bruge sammen med den regneregel som vi netop har bevist gælder: ) ( d dq + q φ E (q) = ɛφ E (q) (( q d ) ( q + d ) ) + 1 φ ɛ (q) = ɛφ ɛ (q) (6.4) dq dq (( q d ) ( q ± d )) φ ɛ (q) = (ɛ 1)φ ɛ (q) dq dq Som det næste skal man bevise at formel 6.4 gælder for og ɛ = 1. Dette problem løses via seperation af de variable. ( q + d ) φ ɛ (q) = 0 dq ( ) q ± d dq φ ɛ (q) = 0 qφ ɛ (q) + dφ ɛ(q) = 0 dq dφ ɛ (q) = qφ ɛ (q) dq 1 φ ɛ (q) dφ ɛ(q) = qdq (6.5) ln(φ ɛ (q)) = 1 q + C φ ɛ (q) = e 1 q +C = Ae 1 q = φ 0 Man benytter sig af den sinrigt logaritmiske regneregel: ln(a) = ln( A e iθ ) = ln( A ) + ln(e iθ ) = ln( A ) + iθ Man får altså φ 0 (q) = Ae 1 q og indsætter man grundtilstanden for ɛ i dennes funktion fra starten får man E 0 = hω, desuden fik vi også en sammenhæng imellem q og x, denne sammenhæng giver: φ 0 (x) = Ae x mω h. Energien er altså E 0, som kan tænkes som grundtilstanden.
33 6.1. OPGAVE H 7 Som det næste tages der udgangspunkt i formel 6.4, hvor man opstiller en egenværdiligning for den n de exciterede tilstand. ( q d ) ( q + d ) (( q d ) ) (( φ n (q) = (ɛ n 1) q d ) ) φ n (q) (6.6) dq dq dq dq Formel 6.6 er skrevet ud fra formel 6.4 (+ +), hvis man nu sammenligner formel 6.6 med formel 6.4 ( + ) ser man at følgende gælder. Ved at sammenligne egenværdiligningen i ligning 6.4 og udtrykket fra ligning 6.6 identificeres ( ) (( ) ( )) q d dq φ ɛ (q), som en egenfunktion til operatoren q + d dq q d dq. Den generelle egenfunktion til dette udtryk er ɛ 1. Egenværdien tilhørende egenfunktionen ( q d dq ) φ ɛ (q) er ɛ n + 1 og dermed opstille følgende: ɛ 1 = ɛ n + 1 ɛ = ɛ n + ɛ = ɛ n + 1 ɛ n+1 = ɛ n + 1 ( ) Man ser at når q d dq operere på egenfunktionen øger den energien tilhørende egenfunktionen. Nu kan man opskrive egenfunktionen for den første exciterede tilstand for hhv. x og q, og deres tilhørende energier. Altså φ 1 (q) plus ɛ 1 og φ 1 (x) plus E 1. Man starter med energierne (husk at ɛ 0 = 1 ): ɛ 1 = ɛ ɛ 1 = = 3 (6.7) E n ɛ n hω E 1 = 3 hω Som det næste kan man nu opstille ligningerne for hhv. φ 1 (q) og φ 1 (x). Vi starter med q som vi beregner ud fra formel 6.5: ( φ 1 (q) = q d ) ( A 0 e 1 q = A 0 q d ) ( e 1 q = A 0 qe 1 q ( qe 1 q)) = qa 0 e e 1 q dq dq Man husker helt fra starten at q x mω h mω φ 1 (x) = x (6.8) (6.9), dette indsat i formel 6.9 giver: mω h A 0e e x h (6.10) Endeligt kan den generelle egentilstand for en 1D harmonisk oscillator φ n (x) udtrykkes ved hjælp af det såkaldte Hermite polynomium af n te orden. Det Hermite polynomium af nte orden er givet ved: ( H n e 1 x x d ) e 1 x dx
34 8 KAPITEL 6. LEKTION 6 Den generelle egentilstand er altså: ( ) mω φ n (x) = A n H n h x e 1 mω h x (6.11) Endeligt kan φ 0 normeres. φ 0 er givet ved formel = Ae x mω h dx = π h π h = A mω = A i mω A e x mω h dx π h π h mω = i A A = i mω (6.1)
35 Kapitel 7 Lektion Opgave I Udregn positions-matrixelementet φ m q φ n. Man benytter sig af Dirac-notation og skabelses- og annihilationsoperatorerne samt ortonormeringsbetingelsen. Skabelses- og annihilationsoperatorerne opstilles nu og q isoleres fra disse: ( q d ) φ n = a n φ n qφ n = a n φ n+1 + dφ n (7.1) dq dq ( q + d ) φ n = b n φ n dφ n dq dq = b nφ n 1 qφ n (7.) Hvis man nu starter med at indsætte skabelsesoperatoren, formel 7.1: φ m a n φ n+1 + dφ n = φ m a n φ n+1 + φ m dφ n dq dq Man indsætter nu annihilationsoperatorerne, formel 7., i det man lige har fundet: φ m a n φ n+1 + φ m b n φ n 1 qφ n = φ m a n φ n+1 + φ m b n φ n 1 φ m q φ n Tænker man nu lidt tilbage ser man at følgende gælder: φ m q φ n = φ m a n φ n+1 + φ m b n φ n 1 φ m qφ n (7.3) φ m q φ n = φ m a n φ n+1 + φ m b n φ n 1 φ m q φ n = 1 ( φ m a n φ n+1 + φ m b n φ n 1 ) φ m q φ n = 1 (a nδ m,n+1 + b n δ m,n 1 ) 9
36 30 KAPITEL 7. LEKTION 7 7. Opgave J Vis, at forventningsværdien af positionen x(t) oscillerer med vinkelfrekvensen ω. Man kan bruge resultatet fra opgave I. Først opstiller man den generelle formel for x(t) : x(t) = Ψ (x, t)xψ(x, t)dx (7.4)
37 Kapitel 8 Lektion Opgave O Løs egenværdiligningen for bevægelsesmængdeoperatoren (ˆp x ) i 1D. Først opstilles ligningen for bevægelsesmængdeoperatoren: ˆp x = h i d dx (8.1) Nu kan man opstille egenværdiligninge for formel 8.3. HUSK NOTATIONEN φ p0,x(x), hvor index x betyder egenværdi for p i x og IKKE en egenværdi for p og x. ˆp x φ p0,x(x) =p 0,x φ p0,x(x) (8.) h dφ p0,x(x) =p 0,x φ p0,x(x) i dx dφ p0,x(x) = h dx i p 0,xφ p0,x(x) 1 φ dφ = h p 0,x(x) p0,x(x) i p 0,xdx 1 φ dφ = h p 0,x(x) p0,x(x) i p 0,x dx ln(φ p0,x(x)) + C = ip 0,xx h e ln(φp 0,x(x))+C =e ip 0,x x h φ p0,x(x) =Ae ip 0,x x h 31
38 3 KAPITEL 8. LEKTION 8 8. Opgave O Løs egenværdiligningen for bevægelsesmængdeoperatoren i 1D. Der er fire ligninger man skal løse for disse ligninger er: ( ˆL x R(r) = L x R(r) = x y z z ) R(r) = 0 (8.3) y ( ˆL y R(r) = L y R(r) = y x z z x ( ˆL z R(r) = L z R(r) = z y ( ( ˆL R(r) = L R(r) = (ˆx y z z )) + y x x y ( ŷ ) R(r) = 0 (8.4) ) R(r) = 0 (8.5) ( x z z x Til at løse disse problemer kan man med fordel anvende følgende formler: ˆ L = ˆ r ˆ p (8.7) ˆ L = h i r ˆL x = h ( i ˆx y z z ) y (8.8) ˆL = ˆL x + ˆL y + ˆL z (8.9) Til at starte med kan man anvende kædereglen for at regne for de tre første ligninger: formel 8.3 til formel 8.5. Vi regner den første og tænker os om for at få de sidste to, hint anvend Lynge note fra tavle R z = dr r dr z hvor r = x + y + z. ( x y R(r) z R(r) ) = 0 y R(r) = z R(r) z y z y y dr(r) dr r z = z dr(r) r dr y y r z = z r y y z x + y + z = z y x + y + z yz = zy = niice (8.10) )) ( ( + ẑ y x x )) ) R(r) = 0 y (8.6) Det samme gøres nu for ˆL y og ˆL z og man får at de giver hinanden hver gang. Hvis man nu udleder formel 8.6: ( ( 0 =ˆx y ) ( + z ) ) ( ( yz R(r) + ŷ z ) ( + x ) ) zx R(r) z y z y x z z x ( ( + ẑ x ) ( + y y x = (y + z z y yz ) ) xy R(r) x y + z + x y z x z + xz x z (8.11) + x + y y x xy x y ) R(r)
39 8.3. OPGAVE P Opgave P Vis, at [ˆx, ŷ] = [ˆp x, ˆp y ] = [ˆx, ˆp y ] = 0 [ˆx, ŷ] ψ = ˆxŷψ ŷˆxψ = xyψ yxψ = 0 (8.1) [ˆp x, ˆp y ] ψ = h x y ψ + h y x ψ = h x y ψ + h y x ψ = 0 (8.13) ( [ˆx, ˆp y ] ψ = ˆxˆp z ψ ˆp z ˆxψ = ˆx h i ) z ψ ˆp z xψ = h i x ψ+ h z i Vi har nu gennem formel 8.1 til formel 8.14 bevist at de gælder. z xψ = hx ( x z ψ h (8.14) Find nu de samtidige egentilstande for x, y og p z. Man starter med at opskrive de tre funktioner man skal bruge. ˆxφ x0,y 0,p z,0 = x 0 φ x0,y 0,p z,0 δ(x x 0 ) (8.15) z ψ x ψ z ) = 0 ŷφ x0,y 0,p z,0 = y 0 φ x0,y 0,p z,0 δ(y y 0 ) (8.16) ˆp z φ x0,y 0,p z,0 = p z,0 φ x0,y 0,p z,0 φ x0,y 0,p z,0 Ae ip z,0 z h (8.17) Formel 8.15 og formel 8.16 blev gennemgået i undervisningen og formel 8.17 re lige blevet regnet i den første del af denne opgave. Disse tre resultater kan nu samles til en samlet funktion, da: når opperatorene kommutere er den samtidige egentilstande givet ved produktet af de enkelte egentilstande. φ x0,y 0,p z,0 8.4 Opgave 7.1 = δ(x x 0 )δ(y y 0 )Ae ip z,0 z h (8.18) En partikel bevæger sig i et 1D potentiale energi felt V (x). Vis at opperatorene som beskriver positionen, momentum og energi opfylder disse tre betingelser: [ˆx, ˆp x ] 0, [ˆx, Ĥx] 0, [ˆp x, Ĥx] 0 Vi starter med at bevise at den første betingelse gælder: ) ( h ψ [ˆx, ˆp x ]ψ =ˆx h (xψ) (8.19) i x i x =x h ψ i x h ( ) x i x ψ + x ψ x = h i ψ = i hψ
40 34 KAPITEL 8. LEKTION 8 Formel 8.19 viser altså at [ˆx, ˆp x ] = i h dette gør så også at start argumentet for denne udregning gælder: i h 0. Som det næste regnes start argument to. [ˆx, Ĥx]ψ =ˆx (( h m x + V (x) =x ( h ψ m x + V (x)ψ = h m = h ψ m x ) ) ψ h + xv (x)ψ xv (x)ψ + x m Formel 8.0 viser altså at [ˆx, Ĥx] = h m for denne udregning gælder: h m 0. ) ψ ( h ) m x + V (x) (ˆxψ) (8.0) ( (xv (x)ψ(x) h )) (xψ) m x ( ψ x + ψ x x dette gør så også at start argumentet Den tredje og sidste vil blot blive stillet op, den vil ikke blive regnet, da det er ALT for mongol! [ˆp x, Ĥx]ψ =ˆp x Ĥ x ψ Ĥx ˆp x ψ (8.1) ) (( ( h = h ) ) i x i x + V (x) ψ ( h ) ) ) (( h m x + V (x) ψ i x 8.5 Opgave L Vis, at, og r??p??h er lineære operatorer. Vis dernæst, at den tænkte operator B defineret ved B??= ikke kan repræsentere en observabel. )
41 Kapitel 9 Lektion Opgave 7.3c [ˆL Vis at, ˆL ] z = 0 ved at anvende: [ˆLx, ˆL ] y = i hˆl z, [ˆLy, ˆL ] z = i hˆl x og [ˆLz, ˆL ] x = i hˆl y. Vi ved desuden at følgende gælder ˆL = ˆL x + ˆL y + ˆL z. Der gives et lille hint som gør det usigeligt lettere at regne. [Â, ˆB] = ÂÂ ˆB ˆBÂÂ = ÂÂ ˆB Â ˆBÂ ˆBÂÂ + Â ˆBÂ Dette hint anvender vi nu til at udregne opgaven: [ˆL, ˆL z ] = [ˆL x + ˆL y + ˆL z, ˆL ] z (9.1) =ˆL x ˆLx ˆLz ˆL x ˆLz ˆLx ˆL z ˆLx ˆLx + ˆL x ˆLz ˆLx + ˆL y ˆLy ˆLz ˆL y ˆLz ˆLy ˆL z ˆLy ˆLy + ˆL y ˆLz ˆLy + ˆL z ˆLz ˆLz ˆL z ˆLz ˆLz ˆL z ˆLz ˆLz + ˆL z ˆLz ˆLz =ˆL x [ˆLx, ˆL ] z + [ˆLx, ˆL ] z ˆLx + ˆL y [ˆLy, ˆL ] z + [ˆLx, ˆL ] z ˆLy + ˆL z [ˆLz, ˆL ] z ( ) ) =ˆL x i hˆl y + ( i hˆl y ˆLx + ˆL ) ( ) y ( i hˆl x + i hˆl x ˆLy =i h ( ˆL x ˆLy ˆL y ˆLx + ˆL y ˆLx + ˆL ) x ˆLy 9. Opgave Q Vis, at R(r) er en samtidig egenfunktion for ˆL x, ˆL y, ˆL z og ˆL med tilhørende egenværdier ˆL x = ˆL y = ˆL z = ˆL = 0. For en sfærisk symmetrisk funktion gælder der at værdien af R er den samme i en giver afstand r fra origo uafhængigt af φ og θ. Derved vil det være muligt at betragte et vilkårligt punkt i r, og derefter genereliseres det for samtlige punkter 35
42 36 KAPITEL 9. LEKTION 9 på kugleoverfladen. ( ˆL x = i h y z z ) y ( ˆL y = i h z x x ) z ( ˆL z = i h x y y ) x ˆL = ˆL x + ˆL y + ˆL z (9.) Først evalueres ˆL x, men da der er tale om en sfærisk symmetri kan ˆL y og ˆL z opnås ved at navngiveakserne anderledes, hvilket kan gøres uden tab af generelitet. Opgavens problem kan nu opstilles ˆL x R(r) = L x R(r) hvor dette skal munde ud i at vise at L x = 0. i h ( y z z y ) R(r) = i h ( y R(r) z R(r) ) z y = i h (y z R(r) z y R(r)) = 0 (9.3) Dermed er det vist af R(r) er egenfunktion for ˆL x, med egenværdi L x = 0. Det tilsvarende kan vises at gælde for hhv. ˆL y og ˆL z. Endelig vises, at R(r) er en egenfunktion for ˆL, med tilhørende egenværdi 0, da man ved at ˆL = ˆL x + ˆL y + ˆL z og at vi just har vist at ˆL x,y,zr(r) = 0. Dermed vises det nu at ˆL R(r) = 0: ˆL R(r) = ˆL xr(r) + ˆL yr(r) + ˆL zr(r) = ˆL x (ˆL x R(r)) + ˆL y (ˆL y R(r)) + ˆL z (ˆL z R(r)) = ˆL x 0 + ˆL y 0 + ˆL z 0 = 0 (9.4) 9.3 Opgave R Vis, at R(r) z r ikke er egenfunktion for ˆL x og ˆL y, men er samtidig egenfunktion for ˆL z og ˆL med tilhørende egenværdier L z = 0 og L = h. Først vises det at R(r) z r ikke er en egenfunktion for ˆL x og ˆL y, at de altså ikke virker! Idet at funktionen R(r) z r ikke skelner om det er x eller y, udregnes der kun for x og resultatet kan overføres til y da man bare drejer sit koordinatsystem. ( ˆL x = i h y z z ) (9.5) y
43 9.3. OPGAVE R 37 Man undersøger omkring R(r) z r er egenfunktion for ˆL x. Derfor er det denne funktion man skal differentiere omkring. For at kunne regne på R(r) z r skal man anvende hintet fra opgaven: R(r)z = R(r) z (9.6) r Ligning 9.6 indsættes nu i ligning 9.5, dette giver: ( ˆL x (R(r)z) = i h y (R(r)z) z (R(r)z) ) z y ( ( = i h y R(r) + z R(r) ) ( z z R(r) )) z y = i h ( y (R(r) + z z R(r)) z y R(r) ) = i hyr(r) Resultatet for ligningerne 9.7 kan overføres til y, som giver: (9.7) ˆL y (R(r)z) = i hxr(r) (9.8) Så R(r)z er ikke egenfunktionen til ˆL x og /eller ˆL y. Nu prøves R(r)z som egenfunktion til ˆL z : ( ˆL z (R(r)z) = i h x (R(r)z) y (R(r)z) ) y x ( ( = i h x z R(r) ) ( + 0 y z R(r) )) (9.9) y x = i h (x z y (R(r) y z x R(r)) = 0 Det vises nu at ˆL (R(r)z) = h (R(r)z). Man ved at der gælder: ˆL = ˆL x + ˆL y + ˆL z. Man har lige udregnet både ˆL x (R(r)z), ˆL y (R(r)z) og ˆL z (R(r)z). På ˆL x (R(r)z) og ˆL y (R(r)z) lader man ˆL x og ˆL y virke på igen. Man indsætter altså den første gangs virkende i en ny funktion: ˆL x (ˆL x (R(r)z)) = ˆL x ( i hr(r)y) ( = i h ( i h) y (R(r)y) z (R(r)y) ) z y = h (y z R(r) z R(r) y z R(r)) = h (R(r)z) (9.10) Ud fra resultatet af ligning 9.10 kan der ses at R(r)z er en egenfunktion for ˆL x. Det samme gør sig gældende for ˆL y, altså: ˆL y(r(r)z) = h R(r)z (9.11)
44 38 KAPITEL 9. LEKTION 9 For ˆL z kan man udregne det således: ˆL z = ˆL z (ˆL z (R(r)z)) = ˆL z 0 = 0 (9.1) Nu kan man finde ˆL da man kender alle de andre ˆL nere: ˆL (R(r)z) = ˆL x(r(r)z) + ˆL y(r(r)z) + ˆL z(r(r)z) = h R(r)z + h R(r)z + 0 = h R(r)z (9.13) Derved er det vist at R(r)z er samtidig egenfunktion for ˆL og ˆL z egenværdier for L = h og L z = 0. med
45 Kapitel 10 Lektion Opgave regning nr. 1 Man ved at følgende gælder: φ l,ml = R l (r)y (θ, φ) (10.1) Hvor R l (r) er den symmetriske og Y l,ml er den harmoniske egenfunktion. Desuden kender man to egenværdiligninger: ˆL φ l,ml = l(l + 1) h φ l,ml (10.) ˆL z φ l,ml = m l hφ l,ml (10.3) Vis, at Y l,ml opfylder samme egenværdiligninger for ˆL og ˆL z som φ l,ml. Dvs. man kan gå fra ˆL (R l (r)y l,ml ) til R(r)ˆL Y l,ml (θ, φ). Man begynder nu med at sammensætte ligning 10.1 og ligning 10. for at den bliver til: ˆL R l (r)y (θ, φ) = l(l + 1) h R l (r)y (θ, φ) (10.4) Vi ved fra sidste gang at en L virkende på en sfærisk symmetrisk funktion giver 0 (ˆL R(r) = 0). Man kan omskrive L virkende på φ til følgende: ˆL (R l (r)y l,ml (θ, φ)) = R l (r)ˆl Y l,ml (θ, φ) + Y l,ml ˆL R l (r) (10.5) = R l (r)ˆl Y l,ml (θ, φ) Dette kan man nu sætte sammen med det vi fandt tidligere, altså sammensættes ligning 10.4 og ligning 10.5: R l (r)ˆl Y l,ml (θ, φ) = l(l + 1) h R l (r)y (θ, φ) (10.6) ˆL Y l,m,l (θ, φ) = l(l + 1) h Y l,ml (θ, φ) Dette resultat viser at Y l,ml opfylder samme egenværdiligning som φl, m l for ˆL og ˆL z. 39
46 40 KAPITEL 10. LEKTION Opgave regning nr. Vis, at φ 1, 1 φ 1,1 er egenfunktion for ˆL, men ikke for ˆL z. Hvilke(n) operator(er) er φ 1, 1 φ 1,1 egenfunktion for? DENNE MAGTER VI IKKE LIGE NU, DERFOR STOPPER VI HER OG GåR OVER TIL OPG. S Opgave S I egentilstandene φ l,ml (r, θ, φ) = R l (r)y l,ml (θ, φ) er den sfærisk symmetriske R l (r) og den tilhørende sfærisk harmoniske Y l,ml (θ, φ) normeret særskilt mht. hhv. r og θ, φ. Bestem de normerede sfærisk harmoniske Y 0,0 (θ, φ) og Y 1,0 (θ, φ). Man må genre lave særskilt normering af det følgende volumen integral. 1 = = π π r=0 r=0 φ=0 θ=0 R(r) r dr Y l,ml R(r) r sin(θ)dθdφdr (10.7) π π φ=0 θ=0 Y l,ml sin(θ)dθdφ Man ved at begge led skal være 1 derfor kan man gøre følgende:
47 Kapitel 11 Lektion Opgave U dr + d R d (rr) dr. Vis, at r dr dr = 1 r Dette er ren matematik. Vi starter med at udregne højre siden af ligningen: 1 d (rr) r dr = 1 ( d r dr(r) + R(r) dr ) (11.1) r dr dr dr = 1 ( dr dr(r) + r d R(r) r dr dr dr + dr(r) ) dr = 1 ( dr(r) ) + r d R(r) r dr dr = r dr dr + d R dr Og dette var jo præcis det vi skulle vise at det skulle give! 11. Opgave V Find såvel de frie (E > 0) som de bundne (E < 0) reelle 1 løsninger til, d u dr = me h u (11.) og overvej i forbindelse med de bundne tilstande betydningen af normeringskravet. Først opstiller vi et gæt for u som vi kan benytte til at udregne ligningerne: u(r) = Ae kr (11.3) 1 Da koefficienterne i differentialligningen er reelle, er den komplekskonjugerede af enhver løsning også en løsning, og derfor kan løsningerne jf. superpositionsprincippet vælges reelle. 41
48 4 KAPITEL 11. LEKTION 11 Man benytter nu ligning 11.3 sammen med det fakt at E > 0: u(r) = Ae kr m E E > 0 k = ±i h (11.4) Ligning 11.4 opskrives nu som en fuldstændig løsning: q u fri = Ae i m E h q r + Be i m E h r (11.5) Man ser at A = B, dette kan nu anvendes til at omskrive ligning 11.4: A = B (11.6) A = A e iθ A = A e iθ (11.7) Ligning 11.6 indsættes nu i ligning 11.5, og der regnes videre: q u fri (r) = A e iθ e i m E h ( u fri (r, θ) = A ( = A = A cos q e iθ e i m E h q r + A e iθ e i m E h r ) q e i m E h r+iθ + e i m E h q r + e iθ e i m E h r q m E h «) r iθ r + θ, A, θ R (11.8) Nu kan man indsætte u(0) = 0 i ligning 11.8: u(0) = A cos(θ) = 0 (11.9) For de bundne gælder der følgende: m E E < 0 k bund = ± h u bund = Ae q m E h q r + Be m E h r (11.10) Hvis man nu benytter sig af grænsebetingelserne u(0) = 0 og lim r u(r) = 0 A = 0 får man: q u(r) = Be m E h r (11.11) Pga. normeringsbetingelsen befaler at u er aftegende får man at følgende gælder: q 1 = Be m E h r dr (11.1) 0
49 11.3. OPGAVE W Opgave W Løs det radiale egenværdiproblem for brintatomet: h d [ u nr,l l(l + 1) h ] m e dr + m e r e u nr,l = E nr,lu nr,l (11.13) 4πɛ 0 r u nr,l(0) = lim r u n r,l(r) = 0 Hint 1 Indfør q r a 0, hvor a 0 = 4πɛ0 h e m e, og γ E e Ry, hvor Ry = 8πɛ 0a 0 = e 4 m e, og omskriv ligning 11.13, dette gøres ved at bruge kædereglen: 3πɛ 0 h h 1 d [ u l(l + 1) h m e a 0 dq + m e q a 0 e 4πɛ 0 qa 0 ] u = Ryγ u (11.14) Ganger igennem med 1 og indsætter det som lige er blevet givet: h e 4 m e d [ u m e 16π ɛ 0 h4 dq + e 4 m e 16π ɛ l(l + 1) h e 4 m ] e u = e4 m e 0 q h 3m e q π ɛ 0 h4 3π ɛ γ u (11.15) 0 h opnås følgende ud- Hvis man dividerer ligning igennem med tryk: e 4 m e 3π ɛ 0 h d [ ] u dr + l(l + 1) q q u = γ u (11.16) u(0) = lim q u(q) = 0 Hint Løse ligning for lille værdi q og større værdi q. Først opstilles ligning med små q, hvor kun de dominerende led bliver bibeholdt: d u l(l + 1) = dq q (11.17) Der gættes på en løsning for u til ligning u(q) = Aq k, dette gæt indsættes nu i ligning og udregnes: Ak(k 1)q k = k(k 1)q k = l(l + 1)q k k = l + 1 l(l + 1) q Aq k (11.18) altså for små q er u(q) Aq l+1. Som det næste kan man regne for store q. Dette gøres ved at opstille en differentialligning, der medtager de to dominerende led for store q. d u dq = γ u (11.19)
50 44 KAPITEL 11. LEKTION 11 Der gættes på en løsning for u til ligning u(q) = Bq kq, dette gæt indsættes nu i ligning og udregnes: Bk e kq = γ Be kq (11.0) k = ±γ løsning til ligning er u(q) = Ce γq + De γq, men da lim q = 0 er C = 0 så u(q) De γq (11.1) Hint 3 Da ovenstående potens- og eksponentialfunktioner dominerer for hhv. numerisk små og numerisk store q-værdier, vil produktet af ovenstående have den rigtige q-afhængighed for såvel q 0 som q. Indføres endvidere faktoren f(q), opnås et udtryk for en generel løsning u(q), der opfylder grænsebetingelserne: u(q) = f(q)q l+1 e γq (11.) Indsæt ligning 11. i ligning og find derved flg. differentialligning for f(q). Men først udregnes d dq (f(g)g l+1 e γq ): f = f(q) og g = q l+1 og h = e γq f = df dq og g = (l + 1)q l og h = γe γq f = d f dq og g = l(l + 1)q l 1 og h = γ e γq (11.3) sammensætter man nu det man har fundet i ligningerne 11.3 finder man: d dq (fgh) = d ( ) d dq dq (fgh) = d dq (f(g h + gh ) + f (gh)) = (f(g h + gh + g h ) + f (g h + gh ) + f (g h + gh ) + f (gh)) = ( l(l + 1)q l 1 e γq + q l+1 γ e γq (l + 1)q l γe γq) f + ( (l + 1)q l e γq q l+1 γe γq) df dq + ( q l+1 e γq) d f dq (11.4) Det endelige udtryk man får i ligning 11.4 kan nu indsættes i ligning 11.16: (l(l + 1)q l 1 e γq + q l+1 γ e γq (l + 1)q l γe γq + q l e γq l(l + 1)q l 1 e γq γ q l+1 e γq )f + ( (l + 1)q l e γq q l+1 γe γq) df dq + ( q l+1 e γq) d f dq = 0 (11.5)
51 11.3. OPGAVE W 45 Forkorter man de led væk som går ud med hinanden får man: g l+1 d f dq + ((l + 1)gl q l+1 γ) df dq + (ql (l + 1)q l γ)f = 0 (11.6) dividerer man ligning 11.6 igennem med q l får man: q d f df + ((l + 1) qγ) + (1 γ(l + 1))f = 0 (11.7) dq dq Ligning 11.7 var præcis det vi gerne ville frem til igennem dette hint. Hint 4 Opskriv f(q) som et polynomium af orden n r. Først opstiller man de tre f(q) er: n r f(q) = a s q s (11.8) s=0 n r n r n r f (q) = sa s q s 1 = sa s q s 1 = (m + 1)a m+1 q m s=0 n r s=1 m=0 (11.9) = (s + 1)a s+1 q s s=0 n r n r f (q) = s(s + 1)a s+1 q s 1 = s(s + 1)a s+1 q s 1 s=0 n r s=1 n r (11.30) = (m + 1)(m + )a m+ q m = (s + 1)(s + )a s+ q s m=0 Ligningerne 11.8 til indsættes nu i ligning 11.7:, dette gøres en af gange for overskuelighedens skyld: For alle hvor det bare er f(q) skal den ganges ind på, men for de andre er det lidt mere trikky, vi tage udgangspunkt i den første udregning og ikke i resultatet. γq df nr dq = γsa s q s s=0 (l + 1) df nr dq = (l + 1)sa s q s 1 = s=0 q d nr f dq = s=0 s(s 1)a s q s 1 = n r m=0 n r m=0 s=0 n r (l + 1)(m + 1)a m+1 q m = (l + 1)(s + 1)a s+1 q s s=0 (11.31) n r m(m + 1)a m+1 q m = s(s + 1)a s+1 q s s=0 (11.3)
52 46 KAPITEL 11. LEKTION 11 Det sindrige som er blevet gjort er at nu står alle summerne som noget med q s dette gør at de kan samles under samme sum tegn, igennem ligning Dem med a s for sig og dem med a s+1 for sig: n r s=0 [{(s(s + 1) + (l + 1)(s + 1))a s+1 + (s(1 γ(l + 1)) γs)a s }q s ] = 0 (11.33) ligning kan omskrives via finten: (1 γ(l + 1)) γs = γ(l + 1) γs = γ(l s) = (γ(l + s + 1) ): n r s=0 [{(s(s + 1) + (l + 1)(s + 1))a s+1 (γ(l + s + 1) )a s }q s ] = 0 (11.34) Nu kan man finde en løsning for a s+1 med en a s faktor: a s+1 = ligning kan nu benyttes til at bestemme γ: γ(l + s + 1) s(s + 1) + (l + 1)(s + 1) a s (11.35) 0 = γ(l + n r + 1) n r (n r + 1) + (l + 1)(n r + 1) γ = 1 n r + l + 1 (11.36) Nu hvor man kender γ kan man opskrive funktionerne for U(q), U(r) og E nr,l: U(q) = p nr,l(q)q l+1 e γq U(r) = Np nr,l(r)q l+1 e Ry E nr,l = (n r + l + 1) r (nr +1+1)ao (11.37)
53 Kapitel 1 Lektion Opgave X Udregn, i enheder af frielektronmasser m e, de reducerede masser af alm. brint, deuterium og tritium. Man starter med at finde den reduceret masse for almindelig brint: 1 = = 1 1 1, = µ B m e m p m e 1, 836 m e 1, 836 m e µ B = Dernæst findes den reduceret masse for deuterium: 1 µ D = 1 m e + 1 m kerne = 1 m e + 1, 836 1, 837 m e (1.1) 1 = m e 3671 m e µ D = m e (1.) Sidst findes den reduceret masse for tritium: 1 µ D = 1 m e + 1. Opgave m kerne = 1 m e + 1 = m e 5498 m e µ D = m e (1.3) Der er givet en radial egenfunktion for kvante stadiet af laveste energi for en elektron med et angulart moment L = l(l + 1) h i et Coulomb potentiale: N er en konstant. u 0,l (r) = Nr l+1 e 47 r (l+1)a 0 (1.4)
54 48 KAPITEL 1. LEKTION a Vis at egenfunktionen, ligning 1.4, opfylder normeringebetingelsen (1 = u 0 0,l (r) dr), når følgende gælder: [ ] l+3 N 1 = (1.5) (l + 1)a 0 (l + )! Man starter med at opstille normeringebetingelsen når formel 1.5 gælder: [ ] l+3 1 = u 0,l (r) 1 dr = r l+ e r (l+1)a 0 dr (1.6) (l + 1)a 0 (l + )! 0 Vi ved fra opgave T, afsnit??, at r k e αr dr = k!. I denne opgave kan 0 α k+1 man betragte k = l + og α = (l+1)a 0. Sætter man nu denne viden sammen finder man at følgende gælder: ( ) l+3 1 (l + )! 1 = ( ) (l + 1)a 0 (l + )! l+3 (1.7) (l+1)a 0 Forkorter man ud i ligning 1.7 finder man at der giver 1 = 1 og der er jo sandt :) b Vis at den mest sandsynlige radius for denne tilstand er givet ved: 0 r ms = (l + 1) a o (1.8) Man kan finde radiusen, r, for denne tilstand ved at differentiere den radiale tilstand funktion i forhold til r. d ( u 0,l (r) ) = 0 (1.9) dr Man indsætter nu ligning 1.6, uden integralet, og udregner for r: ( ( 0 = d ) ) l+3 1 dr (l + 1)a 0 (l + )! rl+ e r (l+1)a 0 (1.10) ( ) l+3 1 d ) = (r l+ e r (l+1)a 0 (l + 1)a 0 (l + )! dr ( ) l+3 ( ) 1 = (l + )r l+1 e r (l+1)a 0 rl+ e r (l+1)a 0 (l + 1)a 0 (l + )! (l + 1)a 0 (l + )r l+1 = rl+ (l + 1)a 0 (l + 1)(l + 1)a 0 = rl+ r l+1 r = (l + 1) a 0
55 1.3. OPGAVE BONUS Dette resultat i ligning 1.10 er det samme som ligning 1.8 og det var jo hvad det skulle give. Hvis at r er 0 i origo og i og hvis abosolut kvadratet er positivt. Så, hvis der findes et toppunkt, er dette derfor en maximum c Vis at den gennemsnitlige radius for denne tilstand er givet ved: r = (l + 3)(l + 1)a 0 (1.11) Det eneste der skal ske i denne opgave er at man skal regne lidt matematik: r = 0 r u o,l (r) dr (1.1) ( ) l+3 1 = r 0 (l + 1)a 0 (l + )! rl+ e r ( ) l+3 1 = r l+3 e r (l + 1)a 0 (l + )! 0 ( ) l+3 1 (l + 3)! = ( (l + 1)a 0 (l + )! = (l + 1)a 0 (l + 3) = (l + 3)(l + 1)a Opgave Bonus 1.1 ) l+4 (l+1)a 0 (l+1)a 0 dr (l+1)a 0 dr Løs egenværdiproblemet Ĥφ( r 1, r ) for Ĥ = Ĥ1 + Ĥ, hvor Ȟiφ i ( r i ) = E i φ i ( r i ), i {1, }. Vi gætter på at problemet er nummerbart, vi behøver ikke nogen begrundelse for denne antagelse, men når den nu alligevel er der kan vi lige så godt benytte os af den: Det er vist at Hamilton opperatoren er seperabel i en sum af to opperatorer. Derfor gætter vi på at φ(r 1, r ) kan seppereres til et produkt af to funktioner φ 1 (r r ) og φ (r ). Ĥ 1 (φ 1 (r )φ (r )) + Ĥ(φ 1 (r )φ (r )) = Eφ 1 (r )φ (r ) φ E 1 φ 1 + φ 1 E φ = Eφ 1 (r )φ (r ) E = E 1 + E
56 50 KAPITEL 1. LEKTION 1
57 Kapitel 13 Lektion Opgave Y Vis at: d b c a f(x, y)dxdy = d b c a f(y, x)dydx (13.1) for f(x, y) = x y. Det man gør er at man regner de to sider hver for sig og til sidst sætter disse lig hinanden og forkorter ud for til sidst at se at de giver 0 = 0. d b d [ ] x 3 b d ( b 3 a 3 c a f(x, y)dxdy = c 3 y ( b 3 a 3 = 3 dy = a ) [ y c ] d = (b3 a 3 )(d a ) 6 nu kan man lave den anden: d b d [ ] y 3 b f(y, x)dydx = c a c 3 x dx = a ( b 3 a 3 ) [ x = 3 c ) dy (13.) 3 ( b 3 a 3 ) ( d c ) = 3 d c ] d = (b3 a 3 )(d a ) 6 c ( b 3 a 3 ) dx (13.3) 3 ( b 3 a 3 ) ( d c ) = 3 disse to ligninger giver sjovt nok hinanden, se ligning (b 3 a 3 )(d a ) 6 = (b3 a 3 )(d a ) 6 (13.4) 51
58 5 KAPITEL 13. LEKTION Opgave 10. Bølgefunktionen Ψ(x 1, x, t) består af to partikler med massen m og den totale energi E i et 1D harmonisk oscilator potnetiale har formen: Ψ(x 1, x, t) = φ(x 1, x, t)e Ē h t (13.5) hvor φ(x 1, x ) opfylder egenværdiproblemet: ( h m x 1 h m x + 1 mω x ) mω x φ = Eφ (13.6) vis ved udskiftning at den følgende funktionopfylder. Såfremt og hvis E = E n + E n er opfyldt. φ(x 1, x ) = φ n (x 1 )φ n (x ) (13.7) Vi ved at for Ĥ = Ĥ1 + Ĥ er den samlede energi for de to lig med summen af de enkelte for hhv. Ĥ 1 og Ĥ. Ligning 13.7 substiteres ind i ligning 13.6: Ĥ 1 φ n (x 1 )φ n (x ) + Ĥφ n (x 1 )φ n (x ) = (E n + E n )φ n (x 1 )φ n (x ) (13.8) φ n (x )Ĥ1φ n (x 1 ) + φ n (x 1 )Ĥφ n (x ) = (E n + E n )φ n (x 1 )φ n (x ) Man ved ud fra den HELT GENERELLE egenværdi problem (Ĥφ = Eφ), dette anvendes på ligning 13.8 for at få: φ n (x )E n φ n (x 1 ) + φ n (x 1 )E n φ n (x ) = (E n + E n )φ n (x 1 )φ n (x ) (13.9) 13.3 Opgave 10.3a 1 E n + E n = E n + E n
59 Kapitel 14 Lektion Opgave 11.4 Opgaven Forklar hvorfor op til 10 elektroner kan tilskrives 3d orbitaler i et atom og hvorfor 14 kan til skrives en 4f orbital: Grundet Paulies udelukkelses princip kan ingen atomer på en gang have det samme magnetiske bane kvantetal og spin kvantetal, m l og m s. Ved kombinatorik ses det derved at antallet af tilstande kan skrives som [m l ] og [m s ]. Da m l { l, l + 1,..., 0,..., l 1, l} og m s { 1, 1 } for en elektron kan antallet af m l -tilstande skrives som (l + 1), og antallet af m s som. Derfor er antallet af elektroner i en orbital med banetal l givet ved: (l + 1) = 4l + (14.1) ligning 14.1 benyttes til at regne for 3d orbitalen når er l = : ( + 1) = 10 for 4f orbitalen er l = 3, dette giver sammen med ligning 14.1: ( 3 + 1) = 14 Bonus 1 Opskriv de mulige kvantetalskombinationer n, l, m l og m s : Kvantetalskombinationer for 3d orbitalen, l = og n = 3: m l /m s 1 1, 1/, 1/ 1 1, 1/ 1, 1/ 0 0, 1/ 0, 1/ 1 1, 1/ 1, 1/, 1/, 1/ 53
60 54 KAPITEL 14. LEKTION 14 Kvantetalskombinationer for 4f orbitalen, l = 3 og n = 4: m l /m s , 1/ 3, 1/, 1/, 1/ 1 1, 1/ 1, 1/ 0 0, 1/ 0, 1/ 1 1, 1/ 1, 1/, 1/, 1/ 3 3, 1/ 3, 1/ Bonus Beregn antallet af atomare elektroner, der kan være kendetegnet ved et givet hovedkvantetal n: Der findes 4l + muligheder, da n = n r + l + 1 kan l højest være givet ved l = n 1, dette medfører: 4l + = 4(n 1) + = 4n
61 Kapitel 15 Lektion Opgave Z Bestem bindingslængden mellem de to atomkerner i et ioniseret brintmolekyle i sin grundtilstand. H + Figur 15.1: To protoner og en elektron med indbyrdes afstande R, r og R r. Hint 1 Først opskrives Ĥ for H+ -ionen med energier regnet i Ry og afstande regnet i Bohr-radier a 0, idet der ses bort fra den kinetiske energi af atomkernerne. Ĥ = h e + e m e 4πɛ 0 R e 4πɛ 0 r e 4πɛ 0 R r (15.1) h : Plank s afledte konstant kvadret ( 6, π [Js]). e : Laplace opperatoren for en elektron. m e : Elektron massen (9, [kg]). ɛ 0 : Vakuumpermittiviteten (8, [F/m]). e : Elementar ladningen (1, [C]). 55
62 56 KAPITEL 15. LEKTION 15 1 Som det næste forlænger man brøkerne på højre siden af ligning 15.1 med 1 via a 0 : Ĥ = a 0 h e a 0 m e + a 0e a 0 4πɛ 0 R a 0e a 0 4πɛ 0 r a 0 e a 0 4πɛ 0 R r (15.) Dernæst udskifter man =, R = R a 0 a 0 og r = r a 0 i ligning 15. for at få målet i Bohr-radier. Ĥ = h e e a 0 m + e a 0 4πɛ 0 R e a 0 4πɛ 0 r e a 0 4πɛ 0 R r Nu indføres Rydberg Ry = e 8πɛ 0a 0, jf. afsnit A.3 (15.3) Ĥ = h e a 0 m + Ry e R Ry r Ry R r (15.4) Nu kna man indføre Ĥ = Ĥ Ry for i sidste ende at kunne opskrive ligning 15.4 mere simpelt. Ĥ h = e a 0 Ry m e + R r R r (15.5) Som det sidste kan man indføre følgende, hvis man husker at a 0 = 4πɛ0 h e m e Ry = e a 0 8πɛ 0 a = e 4πɛ 0 h 0 e m e 8πɛ 0 a = h 0 m e a 0 Ligning 15.5 kan nu opskrives som, ved at man også fjerner alle mærkerne, så man kommer tilbage til hvor man startede: Ĥ = + R r R r (15.6) Hint Opskriv løsningen til den tidsuafhængige Schrödingerligning som en overlejring af to atomare 1s-orbitaler φ, der er centrerede omkring hver sin atomkerne. Benyt uskelneligheden af de to atomkerner til at finde netop to forskellige fysiske løsninger, som i det flg. kaldes de molekylære orbitaler. Den generelle tidsuafhængige Schrödingerligning er: Ĥφ = Eφ (15.7) Man nu skrive sammen til en overlejring af de to atomare 1s-orbitaler: Ψ( r) = c 1 φ(r) + c φ( R r ) (15.8) 1 F står for Farate som er enheden for kapacitans. De tight-binding-kyndige vil genkende dette som en LCAO-tilgang.
63 15.1. OPGAVE Z 57 De to protoner er uskelnelige derfor er der symmetri, med dette kan man udregne forholdet imellem c 1 og c. Dette kan omskrives til: c 1 = c c 1 = c e iδ og c = c 1 e iδ Om dette ved man at følgende gælder: (e iδ ) = 1 e iδ = ±1. Altså må følgende være gældenden: c 1 = ±c. Med denne viden kan man omskrive ligning 15.8 til: ( ) Ψ( r) = c 1 φ(r) ± φ( R r ) (15.9) Hint 3 Normer de to molekylære orbitaler under indførelse af overlapintegralet S mellem de to (reelle) atomare 1s-orbitaler: S = φ(r)φ ( R r ) d 3 r (15.10) R 3 Den generelle normeringbetingelse er: 1 = Ψ d 3 r (15.11) R 3 Man kender Ψ fra forrige hint, dette anvender man nu til at opskrive en forskrift for Ψ : Ψ = c 1 ( φ (r) + φ ( R r ) ± φ(r)φ( R r ) ) (15.1) Man kan nu indsætte ligning i ligning og pille ved det så det kommer til at ligne ligning 15.9: 1 = c 1 φ (r)d 3 r + R 3 c 1 φ ( R r ) ± S R 3 (15.13) Hvis de to kerne ligger oven i hinanden er normerings betingelsen 0 fordi S = 1, hvis de derimod ligger langt fra hinanden er der ikke noget overlap og derved vil S = 0. Hvis man sætter c 1 udenfor volument integralet i begge tilfælde og udfører integralet vil det altid give 1, derfor får man: 1 = c 1 (1 + 1 ± S) Dette kan omskrives til at givet et resultat for c 1 : c 1 = 1 1 ± S c 1 = ± S 1 1 c 1 = (1 ± S) (15.14) Den er gange 1 da fasefaktoren vælges til at være 1.
64 58 KAPITEL 15. LEKTION 15 Hint 4 Bestem E af en elektron i hver af de to molekylære orbitaler: Hint 4a Bestem forventningsværdien for Ĥ af en elektron i en af de to atomare orbitaler under indførelse af den atomare energi E 1s og Coulombintegralet C = φ (r) R R r d3 r = φ ( R r ) 3 R r d3 r (15.15) 3 Den generelle forventningsværdien for Ĥ Ĥ eller er: Ĥ = Ψ Ĥ Ψ (15.16) Hvis man nu indsætter ligning 15.6 i ligning får man: Ĥ = Ψ( r) + R r R r Ψ( r) (15.17) Ĥ = Ψ( Ψ)d 3 r R 3 =c 1 R 3 r Ψ d 3 r R 3 R r Ψ d 3 r + (φ(r) ± φ( R r ))( (φ(r) ± φ( R r )))d 3 r R 3 c ( 1 φ (r) + φ ( R r R r ) ± φ(r)φ( R r ))d 3 r 3 c 1 R R r (φ (r) + φ ( R r ) ± φ(r)φ( R r ))d 3 r 3 + c 1 R R (φ (r) + φ ( R r ) ± φ(r)φ( R r ))d 3 r 3 (15.18) R 3 R Ψ d 3 r I det sidste integrale led kan man gange R ud og så giver hele integralet 1. Nu kan man udskrive ligning til dets fulde udtryk, man deler altså op i en masse integraler og evaluerer disse hver for sig. Husk at integralerne kun afhænger af r, derfor kan alle de led som KUN afhænger af R ganges ud fra
65 15.1. OPGAVE Z 59 integralerne. Ĥ =(1)c 1 φ(r)( )φ(r)d 3 R 3 () + c 1 φ(r)( )(±φ( R r ))d 3 r R 3 (3) + c 1 (±φ( R r )( )φ(r))d 3 r R 3 (4) + c 1 (±φ( R r )( )φ( R r ))d 3 r R 3 (5) c 1 R r φ (r)d 3 r 3 (6) c 1 R r φ ( R r ))d 3 r 3 (7) c 1 R r (±φ(r)φ( R r ))d 3 r 3 (8) c 1 R R r φ (r)d 3 r 3 (9) c 1 R R r φ ( R r )d 3 r 3 (10) c 1 R R r (±φ(r)φ( R r ))d 3 r 3 (11) + c 1 R (15.19) Liging er forventningsværdien for Hamilton. Denne ligning er MEGET lang og ikke specielt pæn, derfor kan man forkorte denne. Hint 4b Bestem Hamilton-matrixelementet mellem de to atomare orbitaler under indførelse af Ẽ 0 = φ(r)( )φ( R r )d 3 r = φ( R r )( )φ(r)d 3 r R 3 R 3 (15.0) samt resonansintegralet A = φ(r) R r φ( R r )d 3 r = φ(r) 3 R R r φ( R r )d 3 r (15.1) 3 Man begynder med at forkorte ligning 15.19, ved at gøre brug af ligning 15.10, ligning 15.15, ligning 15.0 og ligning Linjerne og 3 benytter sig af ligning Linjerne 6 og 8 benytter sig af ligning Linjerne 7 og 10 benytter sig af ligning Linje 1 sammen med linje 5 og linje 4 sammen med linje 9 giver begge energien for en 1s orbital.
66 60 KAPITEL 15. LEKTION 15 Dette giver altså: Ĥ = c 1 ( E 1s ± Ẽ0 C ± 4A + ) R (15.) Hint 4c Bestem E for hver af de to molekylære orbitaler ved at sammensætte a og b. Forventningsværdien for Hamilton er det samme som forventningsværdien for energien. Ĥ ( = E = c 1 E 1s ± Ẽ0 C ± 4A + ) (15.3) R Ligning 15.3 kan yderligere forsimples ved at skrive c 1 ud. Dette gøres gennem ligning 15.14: ( 1 E = E 1s ± Ẽ0 C 4A + ) (1 ± S) R ) (15.4) = 1 1 ± S Man må bare trække R afhænger af R. 1 = ( E 1s ± Ẽ0 C A + R ud, da det overordnet integral overhovedet ikke E 1s ± Ẽ0 C A + R dr E 1s ± Ẽ0 C Adr + R (15.5) Hint 5 Opskriv φ i form af en atomar 1s-orbital fra et brintatom. Man benytter sig af den teori som er gennemgået i ligning 4.18, og stykket skrevet imellem ligning 4.9 og ligning 4.30, for at få den generelle forskrift for φ. Man husker desuden at l = 0 og m l = 0 for en 1s-orbital: φ 0,0 (r, θ, φ) = u 0,0(r) Y 0,0 (θ, φ) (15.6) r Gennem opslag (side 190 og 170) kan man finde forskrifter for u 0,0 (r) og Y 0,0 (θ, φ): u 0,0 (r) = ( ) r e r a 0 (15.7) a0 a 0 1 Y 0,0 (θ, φ) = (15.8) 4π Man kan se i ligning 15.8 at der ikke er nogen θ, φ, derfor er denne enhedsløs. Hvis man nu indsætter ligning 15.7 og ligning 15.8 i ligning 15.6 får man: (Man skal lige huske at 1 a 0 = 1 ) a 0 φ 0,0 (r) = ( ) r a0 a 0 e r a 0 πr = 1 a0 π 1 a 0 e r a 0 = 1 a 3 0 π e r a 0 (15.9)
67 15.1. OPGAVE Z 61 Hint 6 Find bindingslængden R ved at minimere E : Den atomare orbital φ generaliseres nu på følgende form: a 3 φ(r) = π e ar (15.30) hvor variationsparameteren a ) ( tillader φ at adskille sig fra et brintatom 3. Hint 6a Udregn φ(r). i sfæriske koordinater opskrives kun for r-afhængighed, da φ ikke afhænger af θ og φ. = r r + r φ(r) = r ( a) a 3 π e ar + a a 3 π e ar (15.31) Hint 6b Bestem Ẽ0 udtrykt ved S og A. Først opskrives Ẽ0 og resultatet fra ligning anvendes til at identificerer S og A, husk man ved hvad forskriften for hhv A og S er ud fra ligningerne og Ẽ 0 = φ( R r )( )φ(r)d 3 r R 3 ( ) = φ( R a r ) R r ( a) 3 a π e ar + a 3 π e ar d 3 r 3 = φ( R r ) R r aφ(r)d3 r φ( R (15.3) r )a φ(r)d 3 r 3 R 3 = a φ( R r ) R r φ(r)d3 r a φ( R r )φ(r)d 3 r 3 R 3 = aa a S Hint 6c Bestem lim R 0 C ved at rækkeudvikle e ar til første orden omkring R = 0. Taylor siger at: f n (x 0 ) f(x) = (x x 0 ) i (15.33) i! i=0 Man nøjes med at rækkeudvikle e ar til første orden. Dette giver: e ar = 1 + ( a)(r 0) 1 = 1 ar (15.34) 3 De kyndige ud i variationsregning vil genkende denne tilgang.
68 6 KAPITEL 15. LEKTION 15 Man har opgivet at følgende gælder: A = a(1 + ar)e ar C = ( 1 e ar (1 + ar) ) R S = (1 + ar + 13 ) a R e ar (15.35) Indsætter man nu udtrykket man er kommet frem til for rækkeudviklingen fra ligning i det man kender for C i ligning får man: C = (1 (1 ar)(1 + ar)) R = ( 1 (1 + ar ar a R ) ) R = ( ar + a R ) R (15.36) = a + 4a R Nu kan lim R 0 C bestemmes ud fra resultatet i ligning 15.36: lim C a (15.37) R 0 Hint 6d Brug dette til at bestemme E 1s. Man kan opskrive en generel forskrift for energien E 1s : E 1s = φ(r) φ(r) φ(r) r φ(r) a 3 π e ar (15.38) Man kender noget fra ligning 15.31, hvor = φ(r), dette gør at ligning kan omskrives til: E 1s = φ(r) ( a) + a r φ(r) φ(r) r φ(r) (15.39) = (a 1) φ(r) r φ(r) a φ(r) φ(r) nu ved man noget dejligt om C fra ligning E 1s = (a 1) φ(r) r φ(r) a (15.40) Det som står inden i er det samme som lim R 0 C. Forskriften for C generelt er givet i ligning 15.41, hvor hvis R = 0 så står der præcis det samme som i i ligning C = φ(r) R r φ(r) (15.41)
69 15.1. OPGAVE Z 63 Nu da man har vist at det giver C så kan man indsætte det man kender fra ligning Hvilket gør at energien giver: E 1s = (a 1)a a = a a (15.4) Hint 6e Opskriv E for hver af de to molekylære orbitaler. Man starter med at finde det man fandt for E i ligning 15.4, man kender forskriften for E 1s, Ẽ 0, S og A. E = 1 ( ) E 1s ± 1 ± S Ẽ0 C A + R = 1 ( a a ± (aa a S) C A ) + (15.43) 1 ± S R Da bonding har lavere energi end anti-bonding anvendes den øvereste fra ± og og for anti-bonding anvendes den nederste fra ± og. E B = 1 ( a a + (aa a S) C A ) + (15.44) 1 + S R Hvis man nu indsætter det man kender fra ligningerne får man: ( 1 E B = 1 + ( 1 + ar a R ) a a + (a (1 + ar)e ar a (1 + ar + 13 ) ) e ar a R e ar ( 1 e ar (1 + ar) ) ) 4a(1 + ar)e ar + R R (15.45) Nu opstilles tilsvarende et udtryk for anti-bonding: E A = 1 ( a a (aa a S) C + A ) + 1 S R (15.46) Hvis man nu indsætter det man kender fra ligningerne får man: ( 1 E A = 1 ( 1 + ar a R ) a a (a (1 + ar)e ar a (1 + ar + 13 ) ) e ar a R e ar ( 1 e ar (1 + ar) ) ) + 4a(1 + ar)e ar + R R (15.47) Hint 6f Minimer endelig E mht. a og R vha. en computer, og bestem derved bindingslængden. Man minimerer via Maple og kommer frem til: E = 1, 173[Ry] R =, 0033[a 0 ][Bohrradier] a = 1, 38 Se bilag B for at se maple regnearket. (15.48)
70 64 KAPITEL 15. LEKTION 15 Hint 6g Angiv hvilke af de to molekylære orbitaler, der benævnes hhv. bonding og anti-bonding. Har vi gjort ved at vi har navn givet dem som E A og E B. Hint 6h Bestem lim R E, og bestem herefter ioniseringsenergien for elektronen i enheder af ev, idet a 1 for R. Da e ar 0 og R 0 for R fårs: Vi ved at a 1 for R og dermed bliver Ioniseringsenergien er derfor 1 Ryberg. lim = R a a (15.49) lim = 1 (15.50) R Pointen Pointen med hele opgave er at man kan sige noget begavet om det er i bonding eller om det er i anti-bonding at energien er lavest, dette bliver vist på figur 15. Figur 15.: Pointen med denne opgave er at vise at det er i det symmetriske tilfælde at enerigen er lavest, da det er her at elektronen befinder sig imellem to proton kerner. Man har taget udgangspunkt i ligningerne for bølgefunktionen φ: a 3 φ(r) = π e ar og φ( R a 3 R r r ) = e a π a 3 π (15.51) Der er afstanden r imellem de to kerner og man begynder i oppe af y aksen og den D graf der er vist skal forestilles som værende cirkel symmetrisk omkring y.
71 Kapitel 16 Eksamens spørgsmål Eksamen i kvantemekanik er mundtlig, varer ca. 5 minutter pr. studerende med ca. 5 minutters forudgående forberedelse og vil blive bedømt efter syvtrinskalaen. Ved eksaminationen vil der kunne spørges ind til alt inden for pensum, som er lig det gennemgåede stof med tilhørende opgaver 1, jf. kursusoversigten. Ved eksaminationen vil der blive lagt vægt på, om den studerende demonstrerer forståelse af den teori, der knytter sig til eksamensspørgsmålet, og dette vil blive afdækket gennem en dialog med eksaminator og censor. Den studerendes fremlæggelse vil således i det omfang, det skønnes nødvendigt, blive afbrudt af opklarende spørgsmål. Det vil i forbindelse med selve eksaminationen ikke være muligt at støtte sig til medbragte noter. Den studerende vil ved eksaminationens start trække et af flg. spørgsmål, som er besvaret i de efterkommende ti kapitler. DET ER IKKE EN KONKURENCE I AUTISME. 1 Fraregnet ekstraopgaver. 65
72 66 KAPITEL 16. EKSAMENS SPØRGSMÅL
73 Kapitel 17 Opgave 1 Partikel-bølge-dualiteten. Bølgefunktioner, bølgepakker. Schrödingerligningen. Læst i: 1.; 1.3; 1.4 (sidste halve);.1;. og Lynge noter 1; (starter på L1s9) 17.1 Partikel-bølge-dualiteten En hvilken som helst kvantepartikel kan til en hver tid være beskrevet som enten en partikel i et bestemt punkt eller som en bølge, hvor hele partiklen er smurt ud over hele bølgens udbredelse. Man starter med at sige noget om Louis de Broglie, franskmand fra 193. Han postulerede at en partikel med en masse og bevægelsesmængde p kan fungere som en bølge. Dette postulat fremsatte de Broglie på baggrund af Plank s arbejde vedrørende sort-legmestråling og Einstein s beskrivelse af fotoelektrisk effekt. På det tidspunkt var der nemlig ingen sammenhæng imellem partikel og bølge. De Broglie s postulat mundede ud i et udtryk: p = E c = hν c = hν λν = h λ (17.1) p : Bevægelsesmængden. E : Energien. h : Plank s konstant. c : Lysets hastighed. ν : Frekvensen. λ : Bølgelængden. 67
74 68 KAPITEL 17. OPGAVE Bølgefunktioner, bølgepakker Bølgefunktioner er funktioner der indeholder alle oplsyninger om en kvantepatikels bevægelsesegenskaber. Nu da vi har konstateret at der findes en partikel-bølge-dualiteten introduceres en kvantepartikel der besider begge egenskaber. Vi konstruerer en bølgefunktion: Ψ( r, t) (17.) Bølgefunktionen 17. kan man indsætte i en volumen integrale for at finde ud af om kvantepartiklen befinder sig i et volumen V. P V = Ψ( r, t) dv (17.3) V P V : Sandsynligheden for at kvantepartiklen findes i volumenet V. V : Volumenet V. Ψ : Bølgefunktionen. r : Positionen. t : Tiden. Integralet 17.3 svare til at sandsynligheden for at finde kvantepartiklen er størst der hvor modulus 1 for bølgefunktionen er størst. Fra EM kender man til monokromatiske bølger: f( r, t) = Ae i( k r ωt) (17.4) f : Funktion for en monokromatisk bølge. A : Amplituden af bølgen (en eller anden tilfældig konstant). k : Bølgevektor. r : Positionen. ω : Vinkelfrekvens. t : Tiden. Man indsætter nu ligning 17.4 i ligning 17.3 i stedet for bølgefunktionen, for at undersøge hvordan sandsynlighedsfordelingen er. P V = f( r, t) dv = A V (17.5) V Ud fra ligning 17.5 kommer man frem til at sandsynlighed er lige fordelt over hele rummet. Man har altså konstateret at ligning 17.4 ikke er smart at bruge for alle bølger, derfor konstrueres en anden funktion, hvor man skal huske at alle former for funktioner kan beskrives via Fourie integraler. Derfor vælges ligning 17. til at have formen: Ψ( r, t) = A( k)e i( k r ωt) d 3 k (17.6) R 3 1 M = p (R(a)) + (I(a)) for en partikel, a, som befinder sig i punkt (R, I)
75 17.3. SCHRÖDINGERLIGNINGEN 69 Bølgepakker er en overlegring (eller superpunering) af flere bølgefunktioner. Monokromatiske bølger har skarpt definerede ω og k. Hvis man siger at ω og k IKKE er skarpt defineret og undersøger steder med konstruktiv interference, så får man: k r ωt = ( k + d k) r (ω + dω)t dωt = d k r ( ) dω t = r d k k ωt = r (17.7) k ω = V g Det man rent fysik har gjort i ligningerne 17.7 er at man har taget bølgerne for hvert ω og k og lagt oven i hinanden. De steder hvor fasen er ens er der konstruktiv interference, denne interference bevæger sig med gruppe hastigheden, V g Schrödingerligningen I det herrens år 196 fremsatte Erwin Schrödinger en differential ligning bølgefunktionen opfylder. For en fri kvantepartikel i 1D ser differential ligningen således ud: i h h Ψ(x, t) = t m Ψ(x, t) (17.8) x For at teste for om bølgefunktionen kan bruges for en fri kvantepartikel udregnes dispersions relationen. For at kunne udregne dispersions relationen, se afsnit A.1, skal man bruge kvantepartikel ens hastighed, V = dω dk V = p m dω dk = hk hk hk m dω = m dk ω = m, og dens bevægelsesmængde, p = hk. Ud fra disse to kan man også finde den kinetiske energi E = E kin = p m = h k m. Nu mangler man bare en ny 1D ligning for bølgefunktionen: Ψ(x, t) = Ae i(kx ωt) (17.9) Nu kan man indsætte ligning 17.9 i ligning 17.8, man skal huske det man fandt for ω, når det er en PLAN bølge. i h t (Aei(kx ωt) ) = h m x (Aei(kx ωt) ) ω hae i(kx ωt) = h k m Aei(kx ωt) ω h(ψ(x, t)) = E kin (Ψ(x, t)) (17.10) Det man altså har fundet ud af er at man kan finde den kinetiske energi for en bølge, ved at gange ω h med vores bølge.
76 70 KAPITEL 17. OPGAVE 1 Udtryk kan generaliseres til 3D: i h t (Aei( k r ωt) ) = h m (Ae i( k r ωt) ) (17.11) Dette er dog kun gældende for en fri kvantepartikel. Hvis man vil have for en kvantepartikel i alle potentialer skal det se sådan ud: i h ( ) t Ψ( r, t) = h m + V ( r, t) Ψ( r, t) (17.1) Venstre siden er den totale energi for systemet, på højre siden er det første led den kinetiske energi og den andet led er den potentielle energi.
77 Kapitel 18 Opgave Position og bevægelsesmængde. Forventningsværdier og usikkerheder. Heisenbergs usikkerhedsrelation. Læst i: 1.4; 3.; 3.3; 3.5; Position og bevægelsesmængde I den klassiske mekanik kan man bestemme positionen af et legeme med lige så god præsition, som man har lyst til. Dette kan man IKKE i kvantemekanikken. Det gælder for en kvantepartikel at den har en bølgefunktion, som indeholder alle informationer om dens bevægelses egenskaber, denne kalder man for Ψ( r, t), som er en funktion der afhænger af positionen og tiden. Ud fra denne funktion kan man finde hvor det er mest sandsynligt at finde kvantepartikelen. Dette gøres ved at tage integralet af det ønskede volumen element over absolut kvadratet: P (V ) = V P : Sandsynlighedsfunktionen. V : Volumenet. Ψ : Bølgefunktionen. r : Positionen. t : Tiden. Ψ( r, t) dv (18.1) Som en lille side note kan det bemærkes at når Ψ er en overlegring af alle bølgetal (vektorer for 3D) kan dette skrives som: Ψ( r, t) = V A(k)e i( k r ωt) d 3 k (18.) 71
78 7 KAPITEL 18. OPGAVE Sandsynligheds regning gælder kun så længe at kvantepartikelen ikke er lokaliseret. Dvs. bølgefunktionen er delokaliseret lige indtil man måler på dens position, hvorefter man lokaliserer den. Med andre ord kolapser man bølgefunktionen for at fastslå præcis hvor kvantepartikelen befinder sig. Ved hjælp af bølgefunktionen vil man forvente også at kunne afkode information om bevægelsesmængden. Bevægelsesmængden siger Louise de Broglie er givet ved: p = h k (18.3) Hvis man ser på udtrykket 18. i 1D, kan man anvende ligning 18.3 til at omskrive til den efterfølgen ligning, ved at have gjort dette er man gået fra r- til p-rum. r-rummet er for position og p-rum er for bevægelsesmængdne. Ψ(x, t) = 1 h ( p h) A e i( p h x ωt) dp (18.4) Nu indfører man en bølgefunktion for p-rummet, som man senere kan bruge til at opskrive sammenhængen imellem r- og p-rummet ved hjælp af Fourie transformation. ( ) 3 π ( ( p h)) Ψ(p, t) = φ(p, t) = A e iωt (18.5) h Ψ : Den Fourie transformerede Ψ. p : Bevægelsesmængden i 1D. A : Differnetiations konstant. Hvis ligning 18.5 indsættes i ligning 18.4 får man: 1 Ψ(x, t) = (π h) 3 Ved at Fourie transformere ligning 18.6 får man: 1 φ(p, t) = (π h) 3 φ(p, t)e i p h x dp (18.6) px i Φ(x, t)e h dx (18.7) Her af ses det at ligning 18.6 og ligning 18.7 er hinandens Fourie transformerede. Ligesom det gælder for positionen kan sandsynligheden for at finde p et givet sted i p-rummet beregnes som: (Dette gæler for 3D tilfældet) P (V p ) = φ( p, t) dv p (18.8) V p P : Sandsynlighedsfunktionen. V p : Volumenet i p-rummet. φ : Fourie transformerede bølgefunktionen. p : Bevægelsesmængden i lidt flere D. t : Tiden.
79 18.. FORVENTNINGSVÆRDIER OG USIKKERHEDER Forventningsværdier og usikkerheder Forventningsværdien er gennemsnittet for uendeligt mange målinger af en given variabel. I kvantemekanik kan denne beregnes ved at lade en operator virke på bølgefunktionen og derefter gange denne bølgefunktion men sin egen komplekst konjugerede. Dette skrives som: o = Ψ (x, t)ôψ(x, t)dx o = Ψ ô Ψ (18.9) Der er forskellige operatore for forskellige bevægelsesegenskaber. Disse afkoder hver sin egenskab, fx vil h d i dx virkende på en bølgefunktion afkode p. Usikkerheden på en serie af målinger kan beskrives som kvadratroden på variansen: u = ( u u ) (18.10) Dette kaldes også for spredningen og er et mål for hvor langt ved siden af forventningsværdien man kan forvente at ens målinger er i middel. Dette kan overføres til alle andre paramater notations messigt. Ligning bliver brugt i Heisenbergs usikkerheds relation Heisenbergs usikkerhedsrelation I 197 formulerede Werner Heisenberg usikkerhedsrelationen, han modtog senere i 193 nobel prisen for denne relation. Heisenberg s usikkerhedsrelation er givet ved: x p h (18.11) Usikkerhedsrelationen kan eftervises via kommutation. Hvis at [Â; ˆB] 0 er disse ikke kompatible, hvilket vil sige at de ikke kan observeres nøjagtigt samtidigt: [Â; ˆB] = Â ˆB ˆBÂ (18.1) Ved at evaluere ([ˆx; ˆp x ]Ψ(x, t)) kan man eftervise ligning 18.11: (ˆxˆp x ˆp xˆx)ψ(x, t) = ˆxˆp x Ψ(x, t) ˆp xˆxψ(x, t) = x h ) d ( h d Ψ(x, t) xψ(x, t) i dx i dx d dx Ψ(x, t) x h i [ˆx; ˆp x ] = i h = i hψ(x, t) + x h i = i hψ(x, t) 0 d Ψ(x, t) dx (18.13)
80 74 KAPITEL 18. OPGAVE
81 Kapitel 19 Opgave 3 Hamiltonoperatoren. Den tidsuafhængige Schrödingerligning. Overlejringer af egentilstande for Hamiltonoperatoren. Læst i: Lynge Hamiltonoperatoren Vi ved at enhver kvantepartikel er beskrevet med en bølgefunktion, Ψ( r, t). Af denne bølgefunktion kan man afkode position, bevægelsesmængde og energi. Ved at anvende en Hamiltonoperator som man lade virke på bølgefunktionen kan man afkode energien for en kvantepartikel. Måden problemet vil blive grebet an på er at man tager udgangspunkt i det tilsvarende klassiske tilfælde og overfører så meget man kan til det kvantemekaniske tilfælde. Klassisk set er energien givet ved: E tot/mek/sys = E kin + E pot (19.1) Hvor hhv. den kinetiske og den potnetielle energi er givet ved: E kin = 1 mv = p m E pot = V ( r, t) = p p m (19.) Dette kan overføres til det kvantemekaniske tilfælde ved at anvende de operatorer som man kender for hhv. position, r og bevægelsesmængde, p. Man ved at der gælder ˆ r = r og ˆ p = h i. Anvender man det man kender kan man opskrive 75
82 76 KAPITEL 19. OPGAVE 3 den kinetiske og den potentielle energi som: Ê kin = 1 m (ˆ p)(ˆ p) = 1 m Ê pot = V (ˆ r, t) = V ( r, t) ( h i ) ) ( h i = h m (19.3) E mek = h m + V ( r, t) Hvis man nu sammenligner dette resultat med den generelle Schrödingerligning, som er givet ved: i h Ψ t = h m Ψ + V ( r, t)ψ (19.4) får man en ny måde at skrive Schrödingerligningen på: i h Ψ t Ĥ : Hamiltonoperatoren. Ψ : Bølgefunktionen. = ĤΨ (19.5) Ved første øjekast er ligning 19.5 en grim ligning at løse da den både skal differentieres i forhold til tid og sted, men visse tiltage kan gøres så den bliver mere overskuelig at løse, dette kommer under den tidsuafhængige Schrödingerligning. 19. Den tidsuafhængige Schrödingerligning Hvis potentialet hvori vores kvantepartikel befinder sig er uafhængigt af tiden kan man med fordel skrive Ψ som et produkt af en r afhængig del og en tids afhængig del: Ψ( r, t) = φ( r)t (t) (19.6) φ : Egenfunktion. Ψ : Bølgefunktionen. T : Tidsfunktionen. Ligning 19.6 indsættes i ligning 19.5, dette medfører: i h (φ( r)t (t)) = Ĥ(φ( r)t (t)) t i hφ( r) (19.7) t (T (t)) = T (t)ĥφ( r) Nu samles den tidsafhængige del på venstre siden af lighedstegnet og den r afhængige del på højresiden. Dette giver: i h 1 T (t) T (t) t = φ( r)ĥφ( r) 1 (19.8)
83 19.. DEN TIDSUAFHÆNGIGE SCHRÖDINGERLIGNING 77 Nu er venstre siden KUN afhængig af tiden og højresiden er KUN afhængig af positionen, derfor må højre og venstre siden være lige den samme konstant, kaldet E. Dette giver to seperable differentialligninger: i h 1 T (t) = E T T (t) t t = iē T (t) (19.9) h 1 = E Ĥφ( r) = Eφ( r) (19.10) φ( r)ĥφ( r) Ligning 19.9 kan løses ved at gætte på en løsning af formen T (t) = Ae kt, som indsættes i ligning 19.9; kae kt = i Ē h Aekt k = i Ē h, dette giver altså at T (t) = Ae i Ē h t. Så: Ψ( r, t) = φ( r)e i Ē h t (19.11) Endnu vigtigere er resultatet, der fremkom i ligning 19.10, der lige nøjagtig giver os den tidsuafhængige Schrödingerligning er givet ved: Ĥφ E ( r) = Eφ E ( r) (19.1) Ĥ : Hamiltonoperatoren. φ E : Egenfunktionen hørende til egenværdiligningen, som er hele ligning 19.1 E : Egenværdien. Dette er en egenværdiligning for Ĥ med tilhørende egenværdier E og egenfunktioner φ E ( r). Da Ĥ er uafhængig af tiden kan konstanten e i Ē h t ganges på begge sider, hvorved der opnås: e i Ē h t Ĥφ E ( r) = e i Ē h t Eφ E ( r) ĤΨ E ( r, t) = EΨ E ( r, t) (19.13) som stadig er den tidsuafhængige Schrödingerligning, som stadig er en egenværdiligning for Ĥ med de samme egenværdier E med egentilstande Ψ E( r, t). I Dirac notation skrives den tidsuafhængige Schrödingerligning som; Ĥ Ψ E = E Ψ E. E = Ψ E Ĥ Ψ E = Ψ E E Ψ E = E Ψ E Ψ E = E E = Ψ E Ĥ Ψ E = E E = E + E = 0 (19.14) Husk det er underforstået at den første Ψ er kompleks konjugeret. Dermed er konstanten E rent faktisk energien E, som er egenværdien for Ĥ.
84 78 KAPITEL 19. OPGAVE Overlejringer af egentilstande for Hamiltonoperatoren Det man netop har vist er at Ψ E er en egentilstand til Ĥ med energien E. Men den fulde løsning til egenværdiproblemet er en overlejring af forskellige egentilstande med forskellige vægte c(e): (først regnes i det kontinuerte tilfælde) Ψ( r, t) = c(e)ψ E ( r, t)de (19.15) Det antages nu at E er kvantiseret. Dermed kan c(e) skrives som en sum: c(e) = n c n δ(e E n ) (19.16) c : Vægten af hver af de forskellige egentilstande. c n : Ny vægtningskonstant. Kan først findes når man har en begyndelses værdi. δ : Sikre at hver energi (E n ) er nomeret med sin egen konstant c n. E : Energien. E n : Kvantiserede energi. Ligning sikre at hver energi E n er vægtet særskilt med vægten c n. Ligning indsættes i ligning 19.15: Ψ( r, t) = = n c n δ(e E n )Ψ E ( r, t)de n c n Ψ n ( r, t) (19.17) Dermed kan den tidsuafhængige Schrödingerligning også skrives som: Ĥφ n = E n φ n (19.18) En løsning til Schrödingerligningen er dermed en overlejring af seperable egentilstande for Ĥ, da de enkelte seperable løsning til egenværdiproblemet netop er, de enkelte mulige egentilstande. Spektralsætingen Egentilstandene for et systems Ĥ udgør et fuldstændigt sæt af ortonormerbare basisfunktioner for et systems tilstandsrum. Ortonormerbarbetegnelsen er givet ved: Ψ m Ψ n = δ mn (19.19) Det betyder i dette tilfælde at de enkelte egentilstande er ortonomerbare basisfunktioner, der ved særskilt normering kan udspænde hele systemets tilstandsrum, dvs. alle mulige løsninger til Schrödingerligningen.
85 Kapitel 0 Opgave 4 Kvantebrønde. Potentialbarrierer. Tunneleffekten. Læst i: 4.4; 5.1; 5. og Lynge Kvantebrønde Man kan med fordel tage udgangspunkt i opgave D, afsnit 3.1. En af grund principperne indenfor kvantemekanik er at alle tilladte energier for en begrænset kvantepartikel er kvantiseret. Denne begrænsning kan beskrives som en 1D kvantebrønd. En kvantebrønd er et 1D teoretisk potentialebarrierer, hvor en kvantepartikel kan bevæge sige inden i med forskellige bølgetal. Kvantebrønden er omgivet af to potentialebarrierer. I selve kvantebrønden er potentialet 0 og udenfor barriererne springer potentialet til uendeligt. Figur 0.1: Her ses en skitsering af en kvantebrønd, hvor potentialet udenfor brønden er uendeligt og bølgefunktionen udenfor er nul, hvorimod inden i brønden er begge defineret. 79
86 80 KAPITEL 0. OPGAVE 4 kvantepartikelen kan enten befinde sig liggende stille på bunden af brønden eller bevæger den sig frem og tilbage imellem x = 0 og x = L. Denne bevægelse er bestemt ud fra en bølgefunktion som opfylder Schrödingerligningen: i h Ψ ( t = h m ) x + V (x) Ψ (0.1) h : Plank s reducerede konstant. Ψ : Bølgefunktionen. t : Tiden. x : Afstanden. V : kvantepartikelens potentielle energi. Hvis en partikel har en defineret energi, E, har bølgefunktionen for partikel en helt bestem form: Ψ(x, t) = φ(x)e i Ē h t (0.) Hvor φ opfylder energiegenværdiligningen (tidsuafhængige Schrödingerligning): ( h ) m x + V (x) φ = Eφ Ĥφ = Eφ (0.3) Ser man nu på ligning 0.3 og på figur 0.1 kan man drage den konklusion at uden for brønden er egenfunktionen φ lig 0 og inden i brønden er potentialet V (x) = 0. Ud fra denne viden kan man opstille et simplificeret udtryk for energien: E = h k (0.4) m Hvor k bare er en eller anden tilfældig konstant. Hvis man nu indsætter ligning 0.4 i ligning 0.3 og tager højde for at potentialet ikke længere er der, så får man at k kan skrives som: k φ = d φ dx (0.5) Ud fra denne ligning findes der en fornuftig ligning for φ, med dertilhørende grænser: φ(x) = M cos(kx) + N sin(kx), φ(0) = φ(l) = 0 (0.6) Grænsebetingelserne sikre at der ikke sker en pludselig ændring for funktionen lige ved grænserne af brønden, og M og N er bare konstanter. Dette problem og ligning ligner tilforvekslig problemer for en vibrerende partikel, som er givet ved funktionen: φ n (x) = N sin(k n x), k n = nπ L (0.7) I klassisk fysik bruges φ n til at beskrive vibrationerne for en snor og i kvantemekanik bruges φ til at beskrive de bølgefunktioner som en partikel kan have.
87 0.. POTENTIALBARRIERER 81 Hvis man nu prøver at indsætte det klassiske tilfældes k n, fra ligning 0.7 i den kvantemekaniske ligning for energien, ligning 0.4, får man: E n = n π h ml, n = 1,, 3,... (0.8) En partikel med enerigen E n har bølgefunktionen: (udfra ligning 0. og ligning 0.7) Ψ n (x, t) = N sin (k n x) e i Ē h t (0.9) 0. Potentialbarrierer Man kan med fordel tage udgangspunkt i opgave F, afsnit 5.1, hvor man skal regne på potentiale energi for en partikel. Figur 0.: Til venstre ses det klassiske tilfælde hvor en kugle skal over en bakke og til højre ses det kvantemekaniske tilfælde hvor en partikel skal over/igennem. Potentialebarrierer er hvad omgiver en kvantebrønd. Det er disse som sikre at kvantepartiklen ikke bare smutter ud igennem vægen af kvantebrønden. Man kan tænke på en potentialbarrierer som værende en bakke som en kugle skal rulle over. Hvis der ikke er energi nok til at få kuglen til at rulle over, vil den ikke gøre det. Hvis kuglen kun kan rulle i 1D (altså frem og tilbage) og er omgivet af to bakker er dette et klassiske fysisk problem som minder om en kvantebrønd omgivet af to potentialbarriererere. Energien en kvantepartikel skal have for at kunne komme over en potentialbarrierer kan udregnes via ligning 0.8. Potentialbarriereren behøver ikke altid være uendelig, den kan godt have en veldefineret energi, som kan overkommes ved at tilføre kvantepartikelen energi. Potentialet udenfor en potentialebarriare er 0 og inden for er den V B. Altså for en kvantepartikel til at kunne komme over en potentialebarriare skal der gælde at E n > V B. V (x) = { 0 for < x < 0 V B for 0 x L 0 for L < x <
88 8 KAPITEL 0. OPGAVE Tunneleffekten Tunneleffekter er hvad der sker når et kvantepartikel alligevel beslutter sig for at gå igennem potentialebarrieren. Tunneleffekten er et velkendt og veldefineret fenomen, ved at have kendskab til tunnelegenskaberne for fx elektroner kan man lave apparater som et STM. Det meste vedrørende tunnelering burde blive gennemgået i opgave F, men der kommer nu alligevel en kort matematik forklaring på det. Når en kvantepartikel kommer til en potentialebarriare har en valget om den vil reflekteres eller transmiteres. Transmissionen er det interessante for tunnelering. Transmissionen er givet ved: T = A R A I (0.10) A R : Sandsynligheden for refkeltion fra potentialebarrieren. A I : Spiff.
89 Kapitel 1 Opgave 5 Den harmoniske oscillator. Vibrationer i to-atomige molekyler. Læst i: Lynge 6; 7 og Den harmoniske oscillator For at gøre alt lettere for sig selv gøres dette også i 1D. Først opskrives Hamilton: Dernæst opskrives Schrödingerligningen: i h h Ψ(x, t) = t m Ĥ = h m x + 1 mω x (1.1) x Ψ(x, t) + 1 mω x Ψ(x, t) (1.) Man kan se i ligning 1. at potentialet, V (x), er tids uafhængigt, og derfor kan man opskrive den tids uafhængige Schrödingerligning: Ĥφ E (x) = Eφ E (x) (1.3) Se nu løsningen for opgave H, afsnit Vibrationer i to-atomige molekyler Klassisk set gælder der for to atomer at enerigen er beskrevet ved: E = p p ( 1 m m ) 1 kx = p µ + 1 km (1.4) 83
90 84 KAPITEL 1. OPGAVE 5 ( Hvor der gælder at: x 0 og den reducerede masse: µ = 1 m m ) 1. Det man kender for den reducerede masse samt for potentialet, genanvender man i det kvantemekaniske tilfælde for at kunne opskrive Hamilton for en harmonisk oscillator for to atomer: Ĥ = h µ x + 1 kx (1.5) µ : Den reducerede masse som er givet ved: 1 µ = 1 m m. x : Afstanden fra hvile og til hvor atomet er nu. k : fjeder konstanten, men der findes ingen fjeder. Spørgsmål: Hvad tager det to atomige molekyle ikke højde for? Modellen tager kun højde for vibration og dermed IKKE translation og rotation. Den er kun brugbar ved meget små udsving da tilnærmelsen bliver hurtigt meget dårligere ved større udsving (den divergerer). Kan også siges på den måde at ved energier som er meget højere end grundtilstanden der divergerer modellen også, da den er tilnærmet grundtilstanden.
91 Kapitel Opgave 6 Operatorrepræsentanter og disses egenskaber, fuldstændige sæt. Samtidigt målbare observable, kommutatorrelationer. Læst i: Lynge 3; 8 og 3.5; 7.1; 7.3; Operatorrepræsentanter og disses egenskaber, fuldstændige sæt Enhver målbar observabel, [O], fx ( r, p, E,...) har en operatorrepræsentant, [Ô]. Hver O er en egenværdi til Ô, dvs. man kan opstille egenværdiproblemet for en observabel: ÔΨ O = OΨ O (.1) Forventsningsværdien for en observabel O har formen: O = Ψ 0( r, t)ôψ 0( r, t)d 3 r = Ψ 0 Ô Ψ 0 R 3 (.) Et par eksempler på meget anvendte operatorer (som også er observable) er: ˆ r = r og ˆp = h L og Ê = Ĥ = h m + V ( r, t) ( ˆL = ˆL x + ˆL y + ˆL z = y z z ) ( + z y x x ) ( + x z y y x Hvis en observabel er en egenværdi for Ô, med egenfunktionen Ψ O, så måler man altid O. Ô Ψ O = O Ψ O Dette er snedigt, fordi det er den tidsuafhængige Schrödingerligning der bruges. Ô skal opfylde nogle egenskaber, disse egenskaber er: 85 )
92 86 KAPITEL. OPGAVE 6 Lineært Ô(c 1 Ψ 1 + c Ψ ) = c 1 ÔΨ 1 + c ÔΨ (.3) Hvis ikke Ô er lineær så kan superpositionsprincippet ikke gælde og Ô kan ikke virke for en KP. Hermitisk Til en hver observabel hører der en operator Ô, som er den Hermitiske konjugerede: ) Ψ 1 (Ô Ψ = ( Ψ 1 Ô ) Ψ (.4) Operatoren er Hermitisk når den er sin egen Hermitiske konjugerede Ô = Ô : O = Ψ 0 Ô Ψ O = (Ô Ψ0 ) Ψ O = O Ψ 0 Ψ O = O (.5) Af det foregående ses at såfremt Ô ikke er Hermitisk, så er egenværdierne ikke reelle. Egentilstandende skal være seperable i ( r, t) og udgøre et fuldstændigt sæt: Ψ O ( r, t) = T O (t)φ O ( r) (.6) En tilstand kan skrives som en superpostion af egentilstande: Ψ( r, t) = c(o, t)φ O ( r)d 3 O (.7) R 3 ligning.7 for det kontinuerte tilfælde. Ψ( r, t) = n c n (t)φ n ( r) (.8) ligning.8 for det diskrete tilfælde. Hvis ikke Ô s tilstande udgør et fuldstændigt sæt kan de ikke beskrives med veldefineret sandsynlighed c(o, t) og c n ( r). Hvis ikke de er seperable, så er de ikke lineært uafhængige og kan ikke udspænde HELE løsningsrummet.. Samtidigt målbare observable, kommutatorrelationer Samtidigt målbare observable er letter at forklare efter man har forklaret om kommutatorrelationer, derfor startes med dette.
93 .. SAMTIDIGT MÅLBARE OBSERVABLE, KOMMUTATORRELATIONER87 Kommutatorrelationer Heisenberg siger at x og p x ikke kan måles samtidigt. Dette gælder også for y og p y samt z og p z, og dermed er r og p ikke samtidigt målbare. Hvorvidt to observable er samtidigt målbare afgøres af komutatoren. Komutatorrelationen er givet ved: [Â, ˆB] =  ˆB ˆB (.9) hvis [Â, ˆB] = 0 så er de observable A og B samtidigt målbare ergo gælder  ˆB = ˆBÂ. Et eksempel er komutatoren for ˆx og ˆp x, som opskrives [ˆx, ˆp x ]. Som man har set i ligning.9 er der en højreside og en venstreside, man starter med at udregne disse to og derefter sætte dem sammen: ˆxˆp x Ψ O (x, t) = x h Ψ i x ˆp xˆxψ O (x, t) = h i x (Ψx) = h i Ψ + h i x Ψ x h i Ψ = x h Ψ ( h i x i Ψ + h ) i x Ψ x [ˆx, ˆp x ] = i h (.10) Klassisk er h = 0 hvilket medfører at x og p x samtidig målbare. Samtidigt målbare observable Antag nu at φ x0,p 0 er en egenfunktion for x og p x. Altså en kvantepartikel i x 0 med impuls p x. Jf ligning.10 gælder der at: der gælder altså: ˆxφ x0,p 0 = x 0 φ x0,p 0 ˆp x φ x0,p 0 = p 0 φ x0,p 0 (.11) i hφ x0,p 0 = [ˆx, ˆp x ]φ x0,p 0 = ˆxˆp x φ x0,p 0 ˆp xˆxφ x0,p 0 = ˆxp 0 φ x0,p 0 ˆp x x 0 φ x0,p 0 = p 0ˆxφ x0,p 0 x 0 ˆp x φ x0,p 0 (.1) = p 0 x 0 φ x0,p 0 x 0 p 0 φ x0,p 0 = 0 Hvilket viser at en konstant virkende på en funktion giver 0, ergo må funktionen være lig 0. Dette betyder at partiklen p x ikke eksisterer.
94 88 KAPITEL. OPGAVE 6
95 Kapitel 3 Opgave 7 Bevægelsesmængdemoment. Egentilstande for ˆL og ˆL z, radiale bølgefunktioner og sfærisk harmoniske. Spin Læst i: Lynge 9; 10 og Bevægelsesmængdemoment Bevægelsesmængdemoment, L, er klassisk set defineret som: L = r p (3.1) Kvantemekanisk bliver bevægelsesmængdemoment regnet på en tilsvarende måde som i det klassiske tilfælde: ˆ L = ˆ r ˆ p (3.) ˆ L : Operator repræsentanten for bevægelsesmængdemoment. L : Vektor repræsentanten for bevægelsesmængdemoment. ˆ r : Operator repræsentanten for positionen, r = (xˆx, yŷ, zẑ). ˆ p : Operator repræsentanten for bevægelsesmængden, p = h i. Krydsproduktet som er beskrevet i ligning 3. kan udregnes ved at gøre: ˆx ŷ ẑ ˆ L = x y z (3.3) i h x i h y i h z Man udregner dette krys ved at tage og gange x med determinanten for den ruden. Man får altså: ( ( ˆ L = i h ˆx y z z ) ( + ŷ z y x x ) ( + ẑ x z y y )) (3.4) x 89
96 90 KAPITEL 3. OPGAVE 7 Hvert af de indre led ganget med i h giver hhv. ˆ Lx, ˆ Ly og ˆ Lz. Man kan altså omskrive ligning 3.4 til: ˆL = ˆ L x + ˆ L y + ˆ L z (3.5) Man kan vise at ˆ Lx og ˆ Ly ikke kommuterer og derved vise at disse ikke er samtidigt målbare. Vi ønsker altså at vise, at man ikke kan måle bevægelsesmængdemoment i x og y retningen lige godt på samme tid. Det samme kan gøres for ˆ Lz og ˆ Ly og ˆ Lx og ˆ Lz. Men hvis det derimod er ˆL og ˆ Lx,y,x, så kommuterer disse og giver 0, hvilket gør at de KAN måles samtidigt. Tag derfor udgangpunkt opgave 7.3c i afsnit Egentilstande for ˆL og ˆL z, radiale bølgefunktioner og sfærisk harmoniske Når man har løst opgave R, afsnit 9.3, kan man se at følgende gælder: φ( r) = R( r) z r (3.6) hver R( r) er en sfærisk harmonisk funktion, og er en samtidig egenfunktion for ˆL og ˆ Lz. Det kan vises at: ˆL φ( r) = h φ( r) ˆ L z φ( r) = 0 (3.7) derved kan man sige at L = h L x + L y = h (3.8) nærmere kan de ikke bestemmes da de udspænder en cirkle. Envidere kan det vises at: φ ( r) = R( r) x + iy r φ ( r) = R( r) x iy r (3.9) φ : Egenfunktion 1. φ : Egenfunktion. R : En sfærisk symmetrisk funktion afhængende af radius r. og så er egenfunktionen for ˆL og ˆ Lz med L = h og L z = ± h.
97 3.3. SPIN 91 Udfra egenværdiligningerne for ˆL og ˆ Lz samt udtryk 3.9 kan det ses at den samtidige egenfunktion φ(r, θ, φ) kan skrives som et produkt af en sfærisk symmetrisk og en sfærisk harmonisk. φ(r, θ, φ) = R(r)Y (θ, φ). Vi ved at de sfærisk harmoniske opfylder følgende egenværdiligninger for ˆL og ˆ Lz : ˆL Y (θ, φ) = l(l + 1) h Y (θ, φ) ˆ L z Y (θ, φ) = m l hy (θ, φ) (3.10) I det generelle tilfælde viser det sig at bevægelsesmængdemomentet er kvantiseret med: L = l(l + 1) h, l N 0 L z = m l h, m l = { l, l + 1,..., l 1, l} (3.11) Måden man tæller det infamt trælse m l på er: Antag at l = 3 og indsætte dette i m l = { l, l+1,..., l 1, l}: m l = { 3, 3+1, 3+, 3+3, 3, 3 1, 3} man skal altså i i steps af 1 fra l til l. 3.3 Spin En kvantepartikel har et iboende 1 bevægelsesmængdemoment. Dette har ikke nogen klassisk sammenligning, da en punktformig partikel ikke dreje om sig selv, den har ingen udstrækning og derfor kan den ikke dreje om sig selv. Der er tale om et kvantiseret bevægelsesmængdemoment ligesom det var tilfældet for L, og det er karakteriseret ved spinkvantetallet s og det magnetiske spinkvantetal m s. s N 0 og m s = { s, s + 1,..., 0,..., s 1, s} (3.1) Forskellige kvantepartikler har forskellige spinkvantetal og antallet af magnetiske spinkvantetal fortæller hvor mange forskellige tilstande denne kan være i. Fx gælder der for en elektron at s = 1 og derved m s = { 1, 1 }, spin en halv er også kendt som spin op og ned. 1 Iboende som er en fast egenskab ved en ting eller person, og som ligger i dennes natur
98 9 KAPITEL 3. OPGAVE 7
99 Kapitel 4 Opgave 8 Centralpotentialer, herunder reduceret masse. Den radiale Schrödingerligning. Brintatomet, kvantetal. Læst i: Lynge 10 (s 7-10); 11 og 9.1; 9.; 9.5; Centralpotentialer, herunder reduceret masse Hvis man betragtet brint atomet klassisk kan dets mekaniske energi skrives som: ( ) p p E mek = + p e e (4.1) m p m e 4πɛ 0 r Det som står i ( ) er det kinetiske bidrag og det efter er det potentielle bidrag, som også kaldes V. I et referencesystem med et massemidtpunkt i hvile gælder der at størrelse af de to bevægelsesmængder er ens. Altså gælder der at: p p = p e = p (4.) Grundlaget for at man overhovedet må lave tilnærmelsen i ligning 4. er at i forhold til protonen bevæger elektronen sig uendeligt hurtigt og derved fremstår protonen som værende i hvile. Derudover indføres den reducerede masse, µ, for en proton og en elektron. 1 µ = 1 m p + 1 m e = m e + 1 m e = = (4.3) 1836m e 1836m e 1836m e m e Nu hvor man kender µ kan man opstille et simplere udtryk for ligning 4.1: E mek = p e m e 4πɛ 0 r (4.4) 93
100 94 KAPITEL 4. OPGAVE 8 Nu kan man ved hjælp af klassisk mekanik reducerer ligning 4.4 til et 1D tilfælde: e F = V (r) = ˆr (4.5) 4πɛ 0 r F : Kraften. : En eller anden differentiale dims. V (r) : Coulomb-central-potentialet. Nu vil vi vide noget om kraftmomentet τ tot : ) τ tot = r F = (rˆr) ( e 4πɛ 0 r ˆr = 0 (4.6) da krydsproduktet af to parallelle vektorer er lig nul-vektoren. Vi ved desuden at τ tot også er lig den afledte af bevægelsesmængdemomentet. Dermed må der gælde at: τ tot = d L dt = 0 (4.7) Ligning 4.7 fører til at L er en bevægelseskonstant. Fra klassisk mekanik og matematik ved man at følgende gælder: ( L = r p = m r d r ) = konstant (4.8) dt Arealet da som vektoren r(t) overstryger i tidsrummet dt er givet ved: da = 1 r d r (4.9) sammensættes ligning 4.8 og ligning 4.9 ses følgende: (Kepler s anden lov) da dt = 1 ( r d r ) dt ( ) det ses i ligning 4.8 at L d r m = r dt. Nu kan man opstille L på vektor form: = ( ) 1 L = konstant (4.10) m r = rˆr d r dt = d(rˆr) = ṙˆr + r dt ˆr = ṙˆr + r φ ˆφ (4.11) r : En eller anden vektor som angiver retning og størrelse. ˆr : Enheds retnings vektor. ṙ : En anden måde at skrive dr dt. φ : En vinkel i et θ, φ koordinatsystem.
101 4.1. CENTRALPOTENTIALER, HERUNDER REDUCERET MASSE 95 man ved at ligning 4.11 gælder da følgende er gældende: ˆr = cos(φ)ˆx + sin(φ)ŷ ˆφ = sin φˆx + cos(φ)ŷ = d r dφ dˆr dt = dˆr dφ dφ dt (4.1) Man anvender nu det man ved fra ligningerne 4.8 og 4.1 til at opskrive et simplere udtryk for L: ( L = m r d r ) ( ) = m (rˆr) (ṙˆr + r φ ˆφ) = mr φ ˆφ (4.13) dt Jf. ligning 4.8 har bevægelsesmængden p en radiel del p r og en tangentiel del p t. Længden af disse er: p r = mṙ = mv r p t = mr φ = L r (4.14) p r : Den radielle bevægelsesmængde. p t : Den tangentielle bevægelsesmængde. m : Masse. ṙ : En anden måde at skrive dr dt. r : Længden af r. φ : En anden måde at skrive dφ dt. L : Bevægelsesmængdemomentet. v r : Den radielle hastighed. Nu kan den kinetiske energi inden for systemet opskrives: E kin = p m = p r + p t m = 1 ) (m v r + L m r = 1 mv + L m r (4.15) Dermed kan den samlede mekaniske energi skrives som: ( ) 1 E mek = mv + L m e r 4πɛ 0 r = 1 mv r + V egg (r) (4.16) hvor V egg (r) kaldes det effektive centralpotentiale. Dermed er dette klassiske 3D tilfælde kogt ned til et 1D problem, og vi kan GODT lide færre D. Det kvantemekaniske centralpotentiale opskrives ud fra de ting man ved gælder i kvantmekanikken: Ĥφ(r, θ, φ) = E nr φ(r, θ, φ) φ(r, θ, φ) = R(r)Y (θ, φ) ˆL R(r) = 0, ˆL Y (θ, φ) = l(l + 1) h Y (θ, φ) ˆL z R(r) = 0, ˆL z Y (θ, φ) = m l hy (θ, φ) (4.17)
102 96 KAPITEL 4. OPGAVE 8 Ud fra ligningerne 4.17 bestemmes en samtidig egenfunktion, hvor man skal huske at indekserer n r, l og m l, da disse indgår i tre seperable egenværdiproblem for hhv. ˆL, ˆL z og Ĥ. φ nr,l,m l (r, θ, φ) = R nr,l,m l (r)y nr,l,m l (θ, φ) (4.18) Som det næste bliver man nød til at springe lidt rundt i den overordnet opgave og tale lidt om den radiale Schrödingerligning. I Schrödingerligningen indgår operatoren. Det første man gør er at opskrive Laplace i sfæriske koordinater: = r r + r + 1 ( 1 r tan(θ) θ + θ + 1 ) sin (θ) φ (4.19) Der er blevet vist i ekstra opgave fra lektion 11 at følgende gælder: ˆL ( 1 h = tan(θ) θ + θ + 1 ) sin (θ) φ (4.0) Ligning 4.0 indsættes i ligning 4.19 hvorefter man opnår: = r Ved hjælp af ligning 4.1 opstilled Hamilton: Ĥ = h m ( h + V (r) = m r r + r ˆL h r (4.1) r + r ) + ˆL + V (r) (4.) mr Hvis man nu tænker på det tidsuafhængige Schrödinger tilfælde; Ĥφ n r,l,m l = E nr,l,m l φ nr,l,m l, finder man at: Ĥ(R nr,ly nr,l,m l ) = E nr,l,m l (R nr,ly nr,l,m l ) (4.3) Nu indsættes Hamiltonoperatoren i ligning 4.3: ( ( ) h m r r + r + ˆL ) mr V R nr,ly nr,l,m l = E nr,l,m l R nr,ly nr,l,m l (4.4) Dette er en udgave til Schrödingerligningen, men da der stadig er noget vinkel afhængighed, så er det IKKE den radielle udgave, endnu. Nu udregnes de enkelte led af Ĥ virkende på R n r,ly nr,l,m l : ( h m r r + r ) R nr,ly nr,l,ml = h m ( ) R r r + R r Y nr,l,m l +0 (4.5)
103 4.. DEN RADIALE SCHRÖDINGERLIGNING 97 1 mr ˆL (R nr,ly nr,l,m l ) = R n r,l mr ˆL Y nr,l,m l = R n r,l mr l(l + 1) h Y nr,l,m l (4.6) V R nr,ly nr,l,m l = V R nr,ly nr,l,m l (4.7) Nu da man har de tre led udregnet kan de indsættes i ligning 4.4: ( ) h R m r r + R l(l + 1) h r Y nr,l,ml + mr R nr,ly nr,l,m l +V R nr,ly nr,l,m l = E nr,l,m l R nr,ly nr,l,m l (4.8) Man lægger mærke til at alle led afhænger af Y nr,l,m l, derfor kan man dividerer igennem med dette så det forsvinder. Desuden anvender man resultatet fra opgave U, afsnit Disse to ting til sammen giver: h 1 m r (rr nr,l) r + ( l(l + 1) h mr + V ) R nr,l = E nr,l,m l R nr,l (4.9) Der indføres den radielle egenfunktion U(r) = rr nr,l(r) og der ganges igennem med r. Dermed opnås den radielle Schrödingerligning: h ( U l(l + 1) h ) m r + mr + V U = EU (4.30) 4. Den radiale Schrödingerligning Se fra ligning 4.19 og til og med ligning Brintatomet, kvantetal Se opgave W, afsnit Kvantetal givet ved: I opgave W kommer man frem til at energien for et brint atom er Ry E = (n r + l + 1), n r N 0 (4.31) Pga. at både n r og l tilhøre positive hele tal og 0, er der degeneration i energien. Derfor indføres det samlede kvantetal n: n = n r + l + 1 n = 1,, 3,... (4.3) n : Det samlede kvantetal. n r : Det radiele kvantetal. l : Bane kvantetal.
104 98 KAPITEL 4. OPGAVE 8 Dermed kan E, fra ligning 4.30 skrives som: E = Ry n 6 ev = 13, n (4.33) som er det udtryk vi altid har kendt for enerigen for brint. Hvis fx n = 1 medfører at l = 0 og derved har man en 1s-orbital. n = medfører at l = 0 eller l = 1 og derved har man mulighed for både en s- og en p-orbital. Generelt gælder der at: l = 0 s-orbital l = 1 p-orbital l = d-orbital l = 3 f-orbital l = 4 g-orbital l = 5 h-orbital osv. Her angiver n skalnummeret hvori orbitalen befinder sig.
105 Kapitel 5 Opgave 9 Uskelnelige partikler, herunder udvekslingssymmetri. Bosoner og fermioner. Læst i: Lynge 13 og 10.1; 10.; 10.3; Uskelnelige partikler, herunder udvekslingssymmetri Klassisk set kan man kun skelne imellem to ellers identiske partikler, hvis man kender deres start position og deres bevægelse. Kvantemekanisk kan man sige at såfremt to uskelnelige partiklers opholdssandsynlighed overlapper kan man ikke skelne imellem dem, da man ikke kan forudsige deres bevægelse. To partikel-bølgefunktionen To identiske partikler i en partikelbølgefunktion: Ψ( r 1, r, t) (5.1) Sandsynligheden for at finde partikel 1 [p 1 ] i volumenet 1 [V 1 ] og partikel [p ] i volumenet [V ] kan skrives som: p 1, = Ψ( r 1, r, t) d 3 r 1 d 3 r, d 3 r = dxdydz (5.) V 1 V Pga. uskelneligheden gælder der den samme sandsynlighed for at finde p 1 i V 1 som i V og p i V som i V 1. Derfor gælder: V p 1, = p,1 Ψ( r 1, r, t) d 3 r 1 d 3 r = V 1 99 V V 1 Ψ( r, r 1, t) d 3 r 1 d 3 r (5.3)
106 100 KAPITEL 5. OPGAVE 9 ud fra opgave Y, afsnit 13.1, ved man at følgende gælder: Ψ( r 1, r, t) = Ψ( r, r 1, t) (5.4) derfor er sandsynligheden for at finde en partikel omkring r 1 og en anden omkring r. Ud af dette kan der ses at Ψ( r 1, r, t) og Ψ( r, r 1, t) kun kan variere med en fasefaktor e iδ : Ψ( r 1, r, t) = e iδ Ψ( r, r 1, t) e iδ Ψ( r 1, r, t) = Ψ( r, r 1, t) (5.5) Igen pga. uskelneligheden kan man gøre det fiks med bare at bytte rundt på fasefaktoren. Hvis man nu prøver at sammensætte disse to får man: ( e iδ ) Ψ( r1, r, t) = Ψ( r, r 1, t) e iδ = ±1 (5.6) Ψ( r, r 1, t) = ±Ψ( r 1, r, t) { Ψ( r 1, r, t) Ψ( r 1, r, t) symmetrisk anti-symmetrisk dette kan føres videre til en mange partikel bølgefunktion. To identiske vækselvirkende kvantepartikler i en 1D harmonisk oscilator potential Hamiltonoperatoren i 1D for disse partikler er givet ved: Ĥ = h m x mω x 1 h m x + 1 mω x (5.7) For at undersøge udvekslingssymmetrien vil der blive set på dem i samme energiegentilstand og i hver sin energiegentilstand. Samme energiegentilstand Jf. opgave 10., afsnit 13., er partiklernes egentilstand for Hamiltonoperatoren i ligning 5.7 givet ved: Ψ nm (x 1, x, t) = Ψ n (x 1, t)ψ m (x, t) (5.8) og med tiden isoleret (man trækker tiden ud): Ψ n (x 1, t)ψ m (x, t) = φ n (x 1 )e i Ē h t φ n (x )e i Ē h t = φ n (x 1 )φ n (x )e i(n+1)ωt (5.9) Den sidst omskrivning kommer af: E nn = E n = (n + 1 )ω h = (n + 1)ω h, hvor man husker at dette bliver indsat på E og derfor forsvinder h. Det ses så at: Ψ nn ( r, r 1, t) = Ψ nn ( r 1, r, t) (5.10) Det kan konkluderes ad to partikelegentilstanden er symmetrisk når to identiske kvantepartikler er i samme enkeltpartikelegentilstand.
107 5.1. USKELNELIGE PARTIKLER, HERUNDER UDVEKSLINGSSYMMETRI101 Forskellige energiegentilstand Hvis partiklerne er i energiegentilstandende Ψ n og Ψ n findes der to degenereret løsninger: Ψ nn (x 1, x, t) = φ n (x 1 )φ n (x )e i En+E n h t Ψ n n(x 1, x, t) = φ n (x 1 )φ n (x )e i E n +En h t (5.11) hvor energien beregnes til: E nn = E n n = E n + E n = (n + n + 1)ω h. For at gælde skal Ψ nn have udvæksligssymmetrien: Ligning 5.1 er det samme som: Ψ nn (x 1, x, t) = ±Ψ nn (x, x 1, t) (5.1) φ n (x 1 )φ n (x ) = ±φ n (x )φ n (x 1 ) (5.13) Jf figur 6. på side 113 i kvant bogen gælder det ikke da φ 1 (0)φ (1) = 0 φ 1 (1)φ (0). Dette statment kan ses på figuren. Derfor kan det ses at der ikke er udvæksligssymmetri og at Ψ nn og Ψ n n ikke kan udgøre en to partikelegentilstand for de to identiske kvantepartikler. En linearkombination af de to degenerede løsninger Ψ nn og Ψ n n kan være en to partikel egentilstand. Ψ(x 1, x, t) = c 1 Ψ nn (x 1, x, t) + c Ψ n n(x 1, x, t) (5.14) hvor c 1 er sandsynligheden for at p 1 er i tilstand n og p er i tilstand n. c er så sandsynligheden for p 1 er i n og p er i tilstand n. Ud fra nummeringsbetingelsen gælder der at: c 1 + c = 1. Men da partiklerne er uskelnelige må der gælde at: c 1 = c. Ud fra dette kan to linearkombinationer opstilles, en symmetrisk og en anti-symmetrisk. Symmetrisk, c = c 1 = 1 : Ψ S (x 1, x, t) = 1 (φ n (x 1 )φ n (x ) + φ n (x 1 )φ n (x ))e i(n+n +1)ωt (5.15) Anti-symmetrisk, c = c 1 c 1 = 1 og c = 1 : Ψ A (x 1, x, t) = 1 (φ n (x 1 )φ n (x ) φ n (x 1 )φ n (x ))e i(n+n +1)ωt (5.16) Udvækslingskraft Hvis man betragter de to partikler fra før kan deres sandsynlighedstæthed for at være i samme punkt (x 1 = x = x) skrives som: Ψ S (x, x, t) = 1 φ n(x)φ n (x) + φ n (x)φ n (x) = φ n (x)φ n (x) Ψ A (x, x, t) = 0 = Ψ nn (x, x, t) = Ψ n n(x, x, t) (5.17)
108 10 KAPITEL 5. OPGAVE 9 Det kan ses at der i det symmetriske tilfælde er dobbelt sandsyndlighed for at finde partiklerne i samme position i forhold til skelnelig partikler. I det anti-symmetriske tilfælde kan det ses at opholdsandsynligheden er 0. Eftersom partiklerne ikke vækselvirker med hinanden er der ikke nogen klassisk kraft imellem dem, men deres sandsynligheder viser en kvantemekanisk kraft som tiltrækker ved symmetrisk og frastøder ved anti-symmetrisk. Denne kraft kaldes udvæksligskraften. 5. Bosoner og fermioner For at kunne tale om bosoner og fermioner skal man først tale om singlet og triplet tilstande. Jf. kvant lektion 1 har Ψ( r, t) alle informationer om kvantepratiklers bevægelse. Dog har en kvantepartikel også et spin. Hvis bevægelsen og spin er uafhængige gælde der at: Φ n,s,ms = Ψ n χ s,ms (5.18) Φ n,s,ms : Kvantetilstand. Ψ n : Bevægelse χ s,ms : Spin, hvor under der hører spin og magnetisk spin. Der er tre mulige frihedsgrader (n). Betragtes nu to uskelnelige elektroner gælder der at: s = 1 og m s { 1, 1 }. Dette giver spin egentilstandende χ 1, 1 = og χ 1, 1 =. Da spinnet af det samlede system enten kan udslukke eller forstærke hinanden er der to muligheder. s = 1 giver tre mulige projektioner i m s { 1, 0, 1}, dette betyder at det er en triplet tilstand. Triplet tilstand er symmetrisk i en ombytning af partikel index, det er lige meget hvilken rækkefølger man læser m s i, se ligning 5.6. s = 0 giver kun en mulighed i m s = 0 altså er dette en singlet tilstand. Singlet er anti-symmetrisk, se igen ligning 5.6 og forklaring før. Ud fra erkendelsen at spin kan være symmetrisk eller anti-symmetrisk gælder der at der er udvæksligs symmetri imellem bevægelsen og spinnet. Derfor kan man opstille denne tabel: Ψ χ = Φ S S = S Boson S A = A Fermion A S = A Fermion A A = S Boson Bosoner er symmetrisk ved ombytning af partikel index. Fermioner er anti-symmetrisk ved ombytning af partikelens index, og derved overholder de (underforstået fermioner) Paulie s udelukkelses princip, se udvælgelseskraften. Se desuden Lynge 13 for yderligere om bosoner og fermioner.
109 Kapitel 6 Opgave 10 Atomer og molekyler, herunder centralfelttilnærmelsen. Elektronkonfiguration og det periodiske system. Bindingslængden i en H + -ion Læst i: Lynge 14 og Atomer og molekyler, herunder centralfelttilnærmelsen Under antagelsen af centralpotentialet opskrives Hamiltonoperatoren for ĤHe: Ĥ = h 1 m e h m e e 4πɛ 0 r 1 e 4πɛ 0 r + e 4πɛ 0 r r 1 (6.1) Pga. det sidste led, Ĥ He, som både indeholder r 1 og r kan ligning 6.1 ikke løses analytisk. Tilsvarende kan Hamiltonoperatoren for ethvert atom opskrives analogt til den for helium: Ĥ z = z i=1 h i m e + z ze + 4πɛ 0 r i i=1 z z j=i+1 i=1 e 4πɛ 0 r j r i (6.) z : Atom nummeret for det tilfældige atom. r i : Afstanden fra origo og ud til den i de elektron. Igen ses det at der heller ikke i dette udtryk kan løses analytisk pga. summen af fællesledet for interaktionerne elektronerne imellem. Dette problem (både ligning 6.1 og ligning 6.) kan reduceres ved indførelse af centralfelts tilnærmelsen. Denne indføres fordi der gør det muligt at skrive 103
110 104 KAPITEL 6. OPGAVE 10 Ĥ z som en sum af Hamiltonoperatorer for hver enkelt elektron. Dvs.: Ĥ z = z i=1 Ĥ i, Ĥ i = h i m e + V i (6.3) Men hvad er V i? - I centralfeltstilnærmelsen midles påvirkningen af hver enkel alektron for hhv. store og små r. Først vises for små r og dernæst for store r. Figur 6.1: Illustration af lille r i, altså kort afstand fra origo og ud til den i de elektron. Ved små r i antages det at middelpåvirkeningen fra de andre elektroner udligner hinanden, de den over tid påvirkes lige meget fra alle retninger. Derfor er den eneste reelle påvirkning foråsaget af kernen. Potentialet er derfor: V (r ismå ) = zez (6.4) 4πɛ 0 r i Figur 6.: Illustration af store r i, altså store afstand fra origo og ud til den i de elektron. Ved store værdier for r i virker de resterende z 1 elektroner som afskærmning af z 1 positive ladninger i kernen. Dvs. i middel bliver den i de elektron samlet set påvirket af en enkelt positiv elementarladning og det tilhørende potential kan dermed skrives som: e V (r istore ) = (6.5) 4πɛ 0 r i Man kan nu koge de to udtryk, ligning 6.4 og ligning 6.5, ned til et udtryk så store og små r er samlet. Det nye udtryk kommer til at beskrive et potentiale
Kvantemekanik 8 Side 2 af 10 Observable og operatorer. Grundlæggende egenskaber ved operatorrepræsentanter ( ) O= O. (8.4)
 Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Kvantemekanik 8 Side 1 af 10 Opsummering Egenskaber ved operatorrepræsentanter Det blev i KM3-4 vist, at enhver målbar bevægelsesegenskab (observabel) er repræsenteret ved en operator, som for position,
Den klassiske oscillatormodel
 Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Kvantemekanik 6 Side af 8 n meget central model inden for KM er den såkaldte harmoniske oscillatormodel, som historisk set spillede en afgørende rolle i de banebrydende beskrivelser af bla. sortlegemestråling
Youngs dobbeltspalteforsøg 1
 Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
Kvantemekanik Side af Youngs dobbeltspalteforsøg Klassisk beskrivelse Inden for den klassiske fysik kan man forklare forekomsten af et interferensmønster ud fra flg. bølgemodel. x Før spalterne beskrives
Rektangulær potentialbarriere
 Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Kvantemekanik 5 Side 1 af 8 ektangulær potentialbarriere Med udgangspunkt i det KM begrebsapparat udviklet i KM1-4 beskrives i denne lektion flg. to systemer, idet system gennemgås, og system behandles
Kvant 2. Notesamling....Of doom!
 Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Kvant 2 Notesamling...Of doom! Indhold 1 To-partikelsystemer 1 2 Brint 1 3 Perturbation 2 3.1 Udartet perturbationsteori...................... 3 3.2 Zeeman-effekt............................. 4 3.3 Tidsafhængig
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 2016
 Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær eksamen - Forår - 6. Juni 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Heisenbergs Usikkerhedsrelationer Jacob Nielsen 1
 Heisenbergs Usikkerhedsrelationer Jacob Nielsen 1 Werner Heisenberg (1901-76) viste i 1927, at partiklers bølgenatur har den vidtrækkende konsekvens, at det ikke på samme tid lader sig gøre, at fastlægge
Heisenbergs Usikkerhedsrelationer Jacob Nielsen 1 Werner Heisenberg (1901-76) viste i 1927, at partiklers bølgenatur har den vidtrækkende konsekvens, at det ikke på samme tid lader sig gøre, at fastlægge
Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2...
 Introduktion til kvantemekanik Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2... 6 Hvordan må bølgefunktionen se ud...
Introduktion til kvantemekanik Indhold En statistisk beskrivelse... 3 Bølgefunktionen... 4 Eksempel... 4 Opgave 1... 5 Tidsafhængig og tidsuafhængig... 5 Opgave 2... 6 Hvordan må bølgefunktionen se ud...
Minikvant Fysik 22 - nu også med fysik 312 for os aber
 Minikvant Fysik - nu også med fysik 31 for os aber. enrik Dahl hdahl@tdc-broadband.dḳ. Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert
Minikvant Fysik - nu også med fysik 31 for os aber. enrik Dahl hdahl@tdc-broadband.dḳ. Resumé ADVARSEL - dette er et total underground-dokument!. Det er livsfarligt at bruge ukritisk. Der er næsten sikkert
Formelsamling til. Kvantemekanik. 27. marts Dennis Hansen 1
 Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Formelsamling til Kvantemekanik 7. marts 1 Dennis Hansen 1 Indhold 1 Grundlæggende ligninger 4 1.1 Generelt...................................... 4 1. Postulater i kvantemekanik............................
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 2017
 Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 3. Januar 17 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
En sumformel eller to - om interferens
 En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
En sumformel eller to - om interferens - fra borgeleo.dk Vi ønsker - af en eller anden grund - at beregne summen og A x = cos(0) + cos(φ) + cos(φ) + + cos ((n 1)φ) A y = sin (0) + sin(φ) + sin(φ) + + sin
Besvarelser til Calculus Ordinær Eksamen Juni 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Juni 2019 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C
 Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Det teknisk-naturvidenskabelige basisår Matematik 1A, Efterår 2005, Hold 3 Prøveopgave C Opgaven består af tre dele, hver med en række spørgsmål, efterfulgt af en liste af teorispørgsmål. I alle opgavespørgsmålene
Besvarelser til Calculus Ordinær Eksamen Juni 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Juni 08 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Note om Laplace-transformationen
 Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Note om Laplace-transformationen Den harmoniske oscillator omskrevet til et ligningssystem I dette opgavesæt benyttes laplacetransformationen til at løse koblede differentialligninger. Fordelen ved at
Elektromagnetisme 14 Side 1 af 10 Elektromagnetiske bølger. Bølgeligningen
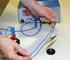 Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Elektromagnetisme 14 Side 1 af 1 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter samt sammenhængen mellem disse felter og de feltskabende ladninger
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 2018
 Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 5. Januar 18 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Matematisk modellering og numeriske metoder. Lektion 10
 Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
Matematisk modellering og numeriske metoder Lektion 10 Morten Grud Rasmussen 2. november 2016 1 Partielle differentialligninger 1.1 Det grundlæggende om PDE er Definition 1.1 Partielle differentialligninger
Kalkulus 1 - Opgaver. Anne Ryelund, Anders Friis og Mads Friis. 20. januar 2015
 Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Kalkulus 1 - Opgaver Anne Ryelund, Anders Friis og Mads Friis 20. januar 2015 Mængder Opgave 1 Opskriv følgende mængder med korrekt mængdenotation. a) En mængde A indeholder alle hele tal fra og med 1
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 2017 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Elektromagnetisme 14 Side 1 af 9 Elektromagnetiske bølger. Bølgeligningen
 Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Elektromagnetisme 14 Side 1 af 9 Bølgeligningen Maxwells ligninger udtrykker den indbyrdes sammenhæng mellem de elektromagnetiske felter. I det flg. udledes en ligning, der opfyldes af hvert enkelt felt.
Besvarelser til Calculus Ordinær Eksamen Juni 2017
 Besvarelser til Calculus Ordinær Eksamen - 12. Juni 217 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 12. Juni 217 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
DesignMat Den komplekse eksponentialfunktion og polynomier
 DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
DesignMat Den komplekse eksponentialfunktion og polynomier Preben Alsholm Uge 8 Forår 010 1 Den komplekse eksponentialfunktion 1.1 Definitionen Definitionen Den velkendte eksponentialfunktion x e x vil
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 2014
 Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Besvarelser til Calculus og Lineær Algebra Globale Forretningssystemer Eksamen - 3. Juni 204 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over
Heisenbergs usikkerhedsrelationer. Abstrakt. Hvorfor? Funktionsrum. Nils Byrial Andersen Institut for Matematik. Matematiklærerdag 2013
 Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Heisenbergs usikkerhedsrelationer Nils Byrial Andersen Institut for Matematik Matematiklærerdag 013 1 / 17 Abstrakt Heisenbergs usikkerhedsrelationer udtrykker at man ikke på samme tid både kan bestemme
Prøveeksamen MR1 januar 2008
 Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
Skriftlig eksamen Matematik 1A Prøveeksamen MR1 januar 2008 Tilladte hjælpemidler Alle sædvanlige hjælpemidler er tilladt (lærebøger, notater, osv.), og også elektroniske hjælpemidler som lommeregner og
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Eksamen i Mat F, april 26 Opgave Lad F være et vektorfelt, givet i retvinklede koordinater som: Udregn F og F: F x F = F x i + F y j + F z k = F y = z 2 F z xz y 2 F = F x + F y + F z = + + x. F = F z
Reeksamen 2014/2015 Mål- og integralteori
 Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Reeksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål. Ved bedømmelsen indgår de spørgsmål med samme vægt.
Anvendelser af den kvantemekaniske bølgemekanik
 Syddansk Universitet, Teknisk Fakultet Anvendelser af den kvantemekaniske bølgemekanik FY529, projekt nr. 2 Skrevet af: Simon Holst Traberg-Larsen;Søren Emil Wegner Petersen d. 24. marts 2013 Resumé el.
Syddansk Universitet, Teknisk Fakultet Anvendelser af den kvantemekaniske bølgemekanik FY529, projekt nr. 2 Skrevet af: Simon Holst Traberg-Larsen;Søren Emil Wegner Petersen d. 24. marts 2013 Resumé el.
MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel
 Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Juni 2000 MATEMATIK 11 Eksamensopgaver Juni 1995 Juni 2001, 4. fjerdedel Opgave 1. (a) Find den fuldstændige løsning til differentialligningen y 8y + 16y = 0. (b) Find den fuldstændige løsning til differentialligningen
Udledning af Keplers love
 Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
Udledning af Keplers love Kristian Jerslev 8. december 009 Resumé Her præsenteres en udledning af Keplers tre love ud fra Newtonsk tyngdekraft. Begyndende med en analyse af et to-legeme problem vil jeg
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: Projekt Trigonometri
 VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
VUC Vestsjælland Syd, Slagelse Nr. 1 Institution: 333247 2015 Anders Jørgensen, Mark Kddafi, David Jensen, Kourosh Abady og Nikolaj Eriksen 1. Indledning I dette projekt, vil man kunne se definitioner
Eksamen i Mat F, april 2006
 Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Eksamen i Mat F, april 26 Opgave 1 Lad F være et vektorfelt, givet i retvinklede koordinater som: F x x F = F x i + F y j + F z k = F y = 2z F z y Udregn F og F: F = F x + F y + F z = 1 + +. F = F z F
Reaktionskinetik - 1 Baggrund. lineære og ikke-lineære differentialligninger. Køreplan
 Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Reaktionskinetik - lineære og ikke-lineære differentialligninger Køreplan 1 Baggrund På 2. eller 4. semester møder kemi/bioteknologi studerende faget Indledende Fysisk Kemi (26201/26202). Her behandles
Matematisk modellering og numeriske metoder. Lektion 8
 Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
Matematisk modellering og numeriske metoder Lektion 8 Morten Grud Rasmussen 18. oktober 216 1 Fourierrækker 1.1 Periodiske funktioner Definition 1.1 (Periodiske funktioner). En periodisk funktion f er
DesignMat Lineære differentialligninger I
 DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
DesignMat Lineære differentialligninger I Preben Alsholm Uge 9 Forår 2010 1 Lineære differentialligninger af første orden 1.1 Normeret lineær differentialligning Normeret lineær differentialligning En
Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
 Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
Komplekse tal Mike Auerbach Odense 2012 1 Vinkelmål og trigonometriske funktioner Inden der siges noget om komplekse tal, vil der i dette afsnit blive gennemgået en smule teori om trigonometriske funktioner.
π er irrationel Frank Nasser 10. december 2011
 π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
π er irrationel Frank Nasser 10. december 2011 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Elementær Matematik. Trigonometriske Funktioner
 Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
Elementær Matematik Trigonometriske Funktioner Ole Witt-Hansen Indhold. Gradtal og radiantal.... sin x, cos x og tan x... 3. Trigonometriske ligninger...3 4. Trigonometriske uligheder...5 5. Harmoniske
DESIGNMAT FORÅR 2012: UGESEDDEL Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til.
 DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
DESIGNMAT FORÅR 2012: UGESEDDEL 13 INSTITUT FOR MATEMATIK 1. Forberedelse Læs alle opgaverne fra tidligere ugesedler, og læg særlig mærke til dem du har spørgsmål til. 2. Aktiviteter mandag 13 17 2.1.
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2)
 Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Noter til KM1 og KM2 på KU (Kvantemekanik 1 og 2) Nikolai Plambech Nielsen, LPK331. Version 1.1 Indhold I Kvant 1 4 1 Bølgefunktionen 4 1.1 Schrödingerligningen....................................... 4
Eksamen i Calculus. Onsdag den 1. juni Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet
 Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Eksamen i Calculus Onsdag den 1. juni 211 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende eksamenssæt består af 7 nummererede sider med ialt
Matematik F Et bud på hvordan eksamenssæt løses
 Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Matematik F Et bud på hvordan eksamenssæt løses Jeppe Trøst Nielsen 11. april 21 Denne samling af ligninger og løsninger er udarbejdet efter det princip, at eksamenssættene ikke ændrer sig specielt meget
Uskelnelige kvantepartikler
 Kvantemekanik 3 Side af 4 Inden for den klassiske determinisme kan man med kendskab til de kræfter, der virker på et partikelsystem, samt begyndelsesbetingelserne for position og hastighed, vha. Newtons
Kvantemekanik 3 Side af 4 Inden for den klassiske determinisme kan man med kendskab til de kræfter, der virker på et partikelsystem, samt begyndelsesbetingelserne for position og hastighed, vha. Newtons
MATEMATIK A-NIVEAU. Kapitel 1
 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik, 01 Kapitel 1 016 MATEMATIK A-NIVEAU Vejledende eksempler på eksamensopgaver og eksamensopgaver i matematik 01
matx.dk Differentialregning Dennis Pipenbring
 mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
mat.dk Differentialregning Dennis Pipenbring 0. december 00 Indold Differentialregning 3. Grænseværdi............................. 3. Kontinuitet.............................. 8 Differentialkvotienten
Mere om differentiabilitet
 Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Mere om differentiabilitet En uddybning af side 57 i Spor - Komplekse tal Kompleks funktionsteori er et af de vigtigste emner i matematikken og samtidig et af de smukkeste I bogen har vi primært beskæftiget
Fysik 2 - Den Harmoniske Oscillator
 Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Fysik 2 - Den Harmoniske Oscillator Esben Bork Hansen, Amanda Larssen, Martin Qvistgaard Christensen, Maria Cavallius 5. januar 2009 Indhold 1 Formål 1 2 Forsøget 2 3 Resultater 3 4 Teori 4 4.1 simpel
Besvarelser til Calculus Ordinær Eksamen Januar 2019
 Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Besvarelser til Calculus Ordinær Eksamen - 14. Januar 19 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har udelukkende
Komplekse Tal. 20. november 2009. UNF Odense. Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet
 Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Komplekse Tal 20. november 2009 UNF Odense Steen Thorbjørnsen Institut for Matematiske Fag Århus Universitet Fra de naturlige tal til de komplekse Optælling af størrelser i naturen De naturlige tal N (N
Løsningsforslag til opgavesæt 5
 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Løsningsforslag til opgavesæt 5
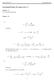 Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Matematik F Matematik F Løsningsforslag til opgavesæt 5 Opgave : Se kursushjemmesiden. Opgave : a) π dθ 5 + 4 sin θ = e iθ, = ie iθ dθ, dθ = i sin θ = eiθ e iθ i = i(5 + 4( / )) = i = + 5i Integranden
Differentiation af Trigonometriske Funktioner
 Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Differentiation af Trigonometriske Funktioner Frank Villa 15. oktober 01 Dette dokument er en del af MatBog.dk 008-01. IT Teaching Tools. ISBN-13: 978-87-9775-00-9. Se yderligere betingelser for brug her.
Matematisk modellering og numeriske metoder. Lektion 11
 Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
Matematisk modellering og numeriske metoder Lektion 11 Morten Grud Rasmussen 5. november 2016 1 Partielle differentialligninger 1.1 Udledning af varmeligningen Vi vil nu på samme måde som med bølgeligningen
n=1 er veldefineret for alle følger for hvilke højresiden er endelig. F.eks. tilhører følgen
 2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
2 Hilbert rum 2. Eksempler på Hilbert rum Vi skal nu først forsøge at begrunde, at de indre produkt rum af funktioner eller følger, som blev indført i Kapitel, ikke er omfattende nok til vores formål.
DOK-facitliste DOK. DOK-facitliste 1
 -facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
-facitliste 1 -facitliste Listens numre refererer til samlingen af supplerede -opgaver (de gamle eksamensopgaver. På listen står næsten kun facitter, og ikke tilstrækkelige svar på opgaverne. [Korrigeret
Fourier transformationen
 MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
MODUL 6 Fourier transformationen Forfattere: Øistein WIND-WILLASSEN & Michael ELMEGÅRD 4. juni 4 Indhold Fourier transformationen 5. Definition og oprindelse.............................. 5.. Funktioner
Oprids over grundforløbet i matematik
 Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
Oprids over grundforløbet i matematik Dette oprids er tænkt som en meget kort gennemgang af de vigtigste hovedpointer vi har gennemgået i grundforløbet i matematik. Det er en kombination af at repetere
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Eksamen i Calculus
 To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
To find the English version of the exam, please read from the other end! Se venligst bort fra den engelske version på bagsiden hvis du følger denne danske version af prøven. Eksamen i Calculus Første Studieår
Integration m.h.t. mål med tæthed
 Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Integration m.h.t. mål med tæthed Sætning (EH 11.7) Lad ν = f µ på (X, E). For alle g M + (X, E) gælder at gdν = g f dµ. Bevis: Standardbeviset: 1) indikatorfunktioner 2) simple funktioner 3) M + -funktioner.
Lineære differentialligningers karakter og lineære 1. ordens differentialligninger
 enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
enote 11 1 enote 11 Lineære differentialligningers karakter og lineære 1. ordens differentialligninger I denne note introduceres lineære differentialligninger, som er en speciel (og bekvem) form for differentialligninger.
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2004
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2004 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
(Prøve)Eksamen i Calculus
 (Prøve)Eksamen i Calculus Sæt 1, april 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende (prøve)eksamenssæt består af 7 nummererede sider
(Prøve)Eksamen i Calculus Sæt 1, april 2011 Første Studieår ved Det Teknisk-Naturvidenskabelige Fakultet og Det Sundhedsvidenskabelige Fakultet Nærværende (prøve)eksamenssæt består af 7 nummererede sider
MATEMATIK A. Indhold. 92 videoer.
 MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
MATEMATIK A Indhold Differentialligninger... 2 Differentialregning... 3 Eksamen... 3 Hvorfor Matematik?... 3 Integralregning... 3 Regression... 4 Statistik... 5 Trigonometriske funktioner... 5 Vektorer
Eksamen 2014/2015 Mål- og integralteori
 Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Eksamen 4/5 Mål- og integralteori Københavns Universitet Institut for Matematiske Fag Formalia Eksamensopgaven består af 4 opgaver med ialt spørgsmål Ved bedømmelsen indgår de spørgsmål med samme vægt
Komplekse tal og algebraens fundamentalsætning.
 Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
Komplekse tal og algebraens fundamentalsætning. Michael Knudsen 10. oktober 2005 1 Ligningsløsning Lad N = {0,1,2,...} betegne mængden af de naturlige tal og betragt ligningen ax + b = 0, a,b N,a 0. Findes
8 Regulære flader i R 3
 8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
8 Regulære flader i R 3 Vi skal betragte særligt pæne delmængder S R 3 kaldet flader. I det følgende opfattes S som et topologisk rum i sportopologien, se Definition 5.9. En åben omegn U af p S er således
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET.. Beregn den retningsafledede D u f(0, 0).
 EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
EKSAMENSOPGAVELØSNINGER CALCULUS 2 (2005) JANUAR 2006 AARHUS UNIVERSITET H.A. NIELSEN & H.A. SALOMONSEN Opgave. Lad f betegne funktionen f(x, y) = x cos(y) + y sin(x). ) Angiv gradienten f. 2) Lad u betegne
Analyse 1, Prøve 4 Besvarelse
 Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Københavns Universitet Prøve ved Det naturvidenskabelige Fakultet juni 2011 1 Analyse 1, Prøve 4 Besvarelse Lad Opgave 1 (50%) M = {T R 2 T er en åben trekant} og lad A : M R være arealfunktionen, dvs.
Diffusionsligningen. Fællesprojekt for FY520 og MM502. Marts Hans J. Munkholm og Paolo Sibani. Besvarelse fra Hans J.
 Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Diffusionsligningen Fællesprojekt for FY50 og MM50 Marts 009 Hans J. Munkholm og Paolo Sibani Besvarelse fra Hans J. Munkholm 1 (a) Lad [x, x + x] være et lille delinterval af [a, b]. Den masse, der er
Differentialligninger. Ib Michelsen
 Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Differentialligninger Ib Michelsen Ikast 203 2 Indholdsfortegnelse Indholdsfortegnelse Indholdsfortegnelse...2 Ligninger og løsninger...3 Indledning...3 Lineære differentialligninger af første orden...3
Lineære 2. ordens differentialligninger med konstante koefficienter
 enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
enote 13 1 enote 13 Lineære 2. ordens differentialligninger med konstante koefficienter I forlængelse af enote 11 og enote 12 om differentialligninger, kommer nu denne enote omkring 2. ordens differentialligninger.
DesignMat Uge 1 Repetition af forårets stof
 DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
DesignMat Uge 1 Repetition af forårets stof Preben Alsholm Efterår 008 01 Lineært ligningssystem Lineært ligningssystem Et lineært ligningssystem: a 11 x 1 + a 1 x + + a 1n x n = b 1 a 1 x 1 + a x + +
Vektorer og lineær regression
 Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Vektorer og lineær regression Peter Harremoës Niels Brock April 03 Planproduktet Vi har set, at man kan gange en vektor med et tal Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden
Additionsformlerne. Frank Villa. 19. august 2012
 Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Additionsformlerne Frank Villa 19. august 2012 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Komplekse tal. Mike Auerbach. Tornbjerg Gymnasium, Odense 2015
 Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Komplekse tal Mike Auerbach Tornbjerg Gymnasium, Odense 2015 Indhold 1 Vinkelmål og trigonometriske funktioner 2 1.1 Radianer................................................ 2 1.2 Cosinus og sinus som
Kvantitative Metoder 1 - Efterår Dagens program
 Dagens program Afsnit 3.1-3.2 Middelværdi -Definition - Regneregler Betinget middelværdi Middelværdier af funktioner af stokastiske variable Loven om den itererede middelværdi Eksempler 1 Beskrivelse af
Dagens program Afsnit 3.1-3.2 Middelværdi -Definition - Regneregler Betinget middelværdi Middelværdier af funktioner af stokastiske variable Loven om den itererede middelværdi Eksempler 1 Beskrivelse af
Førsteordens lineære differentialligninger
 enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
enote 16 1 enote 16 Førsteordens lineære differentialligninger I denne enote gives først en kort introduktion til differentialligninger i almindelighed, hvorefter hovedemnet er en særlig type af differentialligninger,
Kvantitative Metoder 1 - Forår Dagens program
 Dagens program Afsnit 3.1-3.2 Middelværdi -Definition - Regneregler Betinget middelværdi Middelværdier af funktioner af stokastiske variabler Loven om den itererede middelværdi Eksempler 1 Beskrivelse
Dagens program Afsnit 3.1-3.2 Middelværdi -Definition - Regneregler Betinget middelværdi Middelværdier af funktioner af stokastiske variabler Loven om den itererede middelværdi Eksempler 1 Beskrivelse
BEVISER TIL KAPITEL 3
 BEVISER TIL KAPITEL 3 Alle beviserne i dette afsnit bruger følgende algoritme fra side 88 i bogen. Algoritme: Fremgangsmåde til udledning af forskellige regneregler for differentiation af forskellige funktionstyper
BEVISER TIL KAPITEL 3 Alle beviserne i dette afsnit bruger følgende algoritme fra side 88 i bogen. Algoritme: Fremgangsmåde til udledning af forskellige regneregler for differentiation af forskellige funktionstyper
DesignMat Uge 1 Gensyn med forårets stof
 DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
DesignMat Uge 1 Gensyn med forårets stof Preben Alsholm Efterår 2010 1 Hovedpunkter fra forårets pensum 11 Taylorpolynomium Taylorpolynomium Det n te Taylorpolynomium for f med udviklingspunkt x 0 : P
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 2016
 Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Besvarelser til Calculus Ordinær eksamen - Efterår - 8. Januar 16 Mikkel Findinge Bemærk, at der kan være sneget sig fejl ind. Kontakt mig endelig, hvis du skulle falde over en sådan. Dette dokument har
Lektion 1. Tal. Ligninger og uligheder. Funktioner. Trigonometriske funktioner. Grænseværdi for en funktion. Kontinuerte funktioner.
 Lektion Tal Ligninger og uligheder Funktioner Trigonometriske funktioner Grænseværdi for en funktion Kontinuerte funktioner Opgaver Tal Man tænker ofte på de reelle tal, R, som en tallinje (uden huller).
Lektion Tal Ligninger og uligheder Funktioner Trigonometriske funktioner Grænseværdi for en funktion Kontinuerte funktioner Opgaver Tal Man tænker ofte på de reelle tal, R, som en tallinje (uden huller).
Mujtaba og Farid Integralregning 06-08-2011
 Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Indholdsfortegnelse Integral regning:... 2 Ubestemt integral:... 2 Integrationsprøven:... 3 1) Integration af potensfunktioner:... 3 2) Integration af sum og Differens:... 3 3) Integration ved Multiplikation
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 019 Opgave 1 (6 point) En
Fononiske Båndgab. Køreplan Matematik 1 - FORÅR 2005
 Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Fononiske Båndgab Køreplan 01005 Matematik 1 - FORÅR 2005 1 Baggrund Bølgeudbredelse i materialer og medier (som f.eks. luft) er et fænomen, der kendes af alle og som observeres i forskellige former i
Eksamen i Calculus. 14. juni f (x, y, z) = 1 + x 2 + y 2. x 2 + y 2 1 Hele rummet uden z aksen
 Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Eksamen i Calculus Første Studieår ved Det Tekniske Fakultet for IT og Design, Det Sundhedsvidenskabelige Fakultet samt Det Ingeniør- og Naturvidenskabelige Fakultet 14. juni 19 Opgave 1 (6 point) En funktion
Vinkelrette linjer. Frank Villa. 4. november 2014
 Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Vinkelrette linjer Frank Villa 4. november 2014 Dette dokument er en del af MatBog.dk 2008-2012. IT Teaching Tools. ISBN-13: 978-87-92775-00-9. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Introduktion til Laplace transformen (Noter skrevet af Nikolaj Hess-Nielsen sidst revideret marts 2013)
 Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
Introduktion til Laplace transformen (oter skrevet af ikolaj Hess-ielsen sidst revideret marts 23) Integration handler ikke kun om arealer. Tværtimod er integration basis for mange af de vigtigste værktøjer
z + w z + w z w = z 2 w z w = z w z 2 = z z = a 2 + b 2 z w
 Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Komplekse tal Hvis z = a + ib og w = c + id gælder z + w = (a + c) + i(b + d) z w = (a c) + i(b d) z w = (ac bd) + i(ad bc) z w = a+ib c+id = ac+bd + i bc ad, w 0 c +d c +d z a b = i a +b a +b Konjugation
Den homogene ligning. Vi betragter den n te ordens, homogene, lineære differentialligning. d n y dt n. an 1 + any = 0 (1.2) dt. + a1 d n 1 y dt n 1
 1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
1/7 Den homogene ligning Vi betragter den n te ordens, homogene, lineære differentialligning a 0 d n y dt n + a1 d n 1 y dt n 1 hvor a 0,..., a n R og a 0 0. Vi skriver ligningen på kort form som + + dy
Eulers equidimensionale differentialligning
 Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Eulers equidimensionale differentialligning Projektbesvarelse for MM501, udformet af Hans J. Munkholm Differentialligningen September-oktober 2009 For at kunne referere let og elegant gentages differentialligningen
Hans Harhoff Andersen juni 2010 Projekt i numeriske metoder. Resumé
 Hans Harhoff Andersen 20072394 25. juni 2010 Projekt i numeriske metoder Resumé Ved hjælp af en finite difference approksimation og dertilhørende diskretisering af akserne konstrueres matricer for Schrödingerligningen.
Hans Harhoff Andersen 20072394 25. juni 2010 Projekt i numeriske metoder Resumé Ved hjælp af en finite difference approksimation og dertilhørende diskretisering af akserne konstrueres matricer for Schrödingerligningen.
Kapitel 2 Tal og variable
 Tal og variable Uden tal ingen matematik - matematik handler om tal og anvendelse af tal. Matematik beskæftiger sig ikke udelukkende med konkrete problemer fra andre fag, og de konkrete tal fra andre fagområder
Tal og variable Uden tal ingen matematik - matematik handler om tal og anvendelse af tal. Matematik beskæftiger sig ikke udelukkende med konkrete problemer fra andre fag, og de konkrete tal fra andre fagområder
Projektopgave 1. Navn: Jonas Pedersen Klasse: 3.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/ Vejleder: Jørn Christian Bendtsen Fag: Matematik
 Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Projektopgave 1 Navn: Jonas Pedersen Klasse:.4 Skole: Roskilde Tekniske Gymnasium Dato: 5/9-011 Vejleder: Jørn Christian Bendtsen Fag: Matematik Indledning Jeg har i denne opgave fået følgende opstilling.
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker
 Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Fordybelsesprojekt Matematik 2, forår 2005 Potensrækker Arne Jensen 7. 11. marts 2005 1 Indledning I forbindelse med kurset i Reelle og Komplekse Funktioner afholdes et fordybelsesprojekt med et omfang
Noter om komplekse tal
 Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Noter om komplekse tal Preben Alsholm Januar 008 1 Den komplekse eksponentialfunktion Vi erindrer først om den sædvanlige og velkendte reelle eksponentialfunktion. Vi skal undertiden nde det nyttigt, at
Vektorer og lineær regression. Peter Harremoës Niels Brock
 Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
Vektorer og lineær regression Peter Harremoës Niels Brock April 2013 1 Planproduktet Vi har set, at man kan gange en vektor med et tal. Et oplagt spørgsmål er, om man også kan gange to vektorer med hinanden.
