Start pä ny 3D-figur. Tilpas koordinatsystem. Tegn trekant
|
|
|
- Bjarne Holm
- 9 år siden
- Visninger:
Transkript
1 Intro til nspire_3d.tns Dokumentet nspire_3d.tns gär det meget hurtigere at tegne figurer til gymnasiets rumgeometri. Nyeste version kan downloades fra Start pä ny 3D-figur 1) Hvis du vil tegne en figur ved hjålp af nspire_3d.tns, kan du starte med at gäre det der stçr i 2) - 6) nedenfor. 2) Start det Nspire-dokument hvor du vil tegne figuren. 3) Ébn dokumentet nspire_3d.tns. 4) I sideoversigten til venstre: FÄrst klik pç titlen Nspire 3D, sç häjreklik pç titlen Nspire 3D, VÅlg KopiÑr. 5) Skift til dit eget dokument. 6) I sideoversigten til venstre: FÄrst klik pç en titel, sç häjreklik pç titlen, vålg IndsÄt. Tilpas koordinatsystem 7) Ved at udfäre punkterne 8)-10) kan du tilpasse koordinatsystemet sç det kan bruges i nåste opgave som gçr ud pç at tegne trekanten med vinkelspidser A(0,0,9), B(0,8,0) og C(4,0,0). 8) I dit eget dokument: Klik et tomt sted i 3D-vinduet til häjre. 9) Ébn vårktäjsmenuen VÅlg OmrÅde/zoom og OmrÅdeindstillinger. 10) Hvis vi for alle akser vålger grånserne 10 og 10, sç er bçde A, B og C inden for omrçdet. Tast koordinataksernes grånser. Du kan nçr som helst Åndre disse grånser. Du behäver aldrig taste andre tal i de tre nederste felter. Gradtallene i de to nåstsidste felter Åndres nçr du drejer figuren med musen. Tallet i nederste felt Åndres nçr du trykker pç < eller > hvorved figuren bliver mindre eller stärre. Tegn trekant 11) I det venstre vindue: Tast i et matematikfelt: Tast enter. SÇ fremkommer trekanten. De ni tal i parentesen er de tre koordinatsåt A(0,0,9), B(0,8,0) og C(4,0,0). 12) Skjul trädnettet ved at gäre fälgende: - Klik et tomt sted i 3D-vinduet. - FÄr markären hen til trekanten sç den skifter udseende (ses ikke pç figuren her). - HÄjreklik og vålg Attributter. - FÄrst klik i det Äverste felt, sç klik pç den lille sorte pil til häjre for feltet. SÇ fçs 13) Husk at dokumentet skal gemmes jåvnligt. 14) Drej figuren ved at tråkke med musen, og se den fra mange sider. Denne trekant er nem at fç overblik over, men normalt kan figuren ikke erstattes af nogle skårmklip: Det er nädvendigt at kunne dreje den og se den fra mange vinkler. 15) VÅlg en anden farve til trekanten ved at klikke et tomt sted i 3D-vinduet og färe markären til trekanten sç denne Åndrer udseende, og derefter häjreklikke og vålge Farve. 16) Start pç en ny 3D-figur som beskrevet i 2) - 6). Tegn en figur der ligner kråmmerhuset til häjre, ved at tegne fire trekanter. Kommandoen p1:=trekant(x 1,y 1,z 1,x 2,y 2,z 2,x 3,y 3,z 3 ) tegner trekanten med vinkelspidser (x 1,y 1,z 1 ), (x 2,y 2,z 2 ) og (x 3,y 3,z 3 ). Intro til nspire_3d.tns Side 1 af Karsten Juul
2 Tegn Kugle 17) Tegn kuglen med centrum (0, -30, 0) og radius 25 ved at gäre det der stçr i 18)-21) 18) Start med det der stçr i 2) - 10) bortset fra du i stedet for tallene -10, 2, 10 skal taste andre tal sç der bliver plads til kuglen, f.eks. -60, 10, ) I venstre vindue: Tast i et matematikfelt hvor der i parentesen stçr fire tal med komma imellem, og hvor de tre färste er centrums koordinater, og det sidste er radius. Tryk pç enter. SÇ fremkommer kuglen. 20) Drej figuren ved at tråkke med musen. En drejelige figur pç skårmen kan ikke erstattes af nogle skårmklip: Det er nädvendigt at kunne dreje den og se den fra mange vinkler. 21) Giv kuglen en ny farve ved at fälge anvisningen i 15). 22) En kugle har centrum C(3,3,0). Punktet P(2,2,0) ligger pç kuglen. Tegn kuglen ved at gäre fälgende: Tegn punkt Tast hvor der i parentesen stçr centrums koordinater efterfulgt af P 's. 23) Tegn punkterne A(4,0,0), B(2,2,2) og C(0,4,4) ved at tegne dem som kugler med lille radius. 24) VÅlg ny linjefarve for punkterne. (For at vålge Äverste punkt med mus: Drej figur sç punktet ikke er når kant). 25) Drej figuren til du har overblik over hvordan punkterne ligger. 26) Tegn punktet (2, 3,2) med metoden fra 23). 27) Tegn stativ til dette punkt ved at taste hvor der i parentesen stçr punktets koordinater. 28) For at Åndre stativets farve mç du färst udpege stativet. Det kan du ikke gäre med musen, da stativet er for tyndt. I stedet kan du gäre fälgende: - Klik et tomt sted i 3D-vinduet - Ébn vårktäjsmenu - VÅlg Grafindtastning/Rediger - Klik pç - VÅlg den färste graf (hvis du bruger p1 ) - HÄjreklik et tomt sted og vålg Farve / Linjefarve - Osv. 29) PÇ figuren fra 27) skal du tilfäje punktet (1, 1,3) med stativ. 30) PÇ figuren fra 29) skal du tilfäje et punkt som ligger pç linje med de to andre punkter. Du skal ogsç tegne dette punkts stativ. 31) Husk at dokumentet skal gemmes jåvnligt. Kommandoen p1:=kugle_cr(x,y,z,r) tegner kuglen som har centrum (x,y,z) og radius r. Kommandoen p1:=kugle_cp(x,y,z,x 1,y 1,z 1 ) tegner kuglen som har centrum (x,y,z) og gçr gennem (x 1,y 1,z 1 ). Kommandoen p1:=stativ(x,y,z) tegner et stativ der viser hvor punktet (x,y,z) er i koordinatsystemet. I stedet for p1 kan bruges p2, p3 osv. til p12. BEMáRK at p13-p15 ikke kan bruges til stativ! Intro til nspire_3d.tns Side 2 af Karsten Juul
3 Tegn parallelogram 32) Der er givet punkterne A(0,0,3), B(0,2,0) og C(0,4,0). Figuren viser et parallelogram ABCD. Tegn parallelogrammet ved at gäre det der stçr i 33) - 35). Du skal IKKE skrive bogstaverne A, B, C, D pç figuren. I 70) stçr hvordan jeg har fçet skrevet bogstaverne). 33) GÄr det der stçr i 2) 6). 34) Tast i et matematikfelt hvor der i parentesen stçr de ni tal der er koordinaterne til A, B og C skrevet i råkkefçlge som när vi kçrer rundt om parallelogrammet, dvs. ABC eller CBA, IKKE ACB eller CAB. 35) GÄr det der stçr i 12). Tegn firkant 36) Der er givet punkterne A(0,0,4), B(2,0,0), C(2,4,0) og D(1,3,2). Tegn firkanten ABCD ved at gäre det der stçr i 37) 38). Du skal IKKE skrive bogstaverne A, B, C, D. 36) Tast i et matematikfelt hvor der i parentesen stçr de 12 tal der er koordinaterne til A, B, C og D skrevet i råkkefçlge som när vi kçrer rundt om firkanten. (Hvis de fire punkter ikke ligger i samme plan, sç hedder den tegnede figur ikke en firkant selv om den har fire kanter). 37) Fjern trçdene inden i firkanten, og vålg gerne en anden farve. Se evt. 12) og 15). Tegn vektor (pil) 38) Tegn vektoren afsat ud fra punktet (0,0,4) ved at se i 39) og 40). 39) Tast fälgende hvor der i parentesen färst skal stç begynd-punktets koordinater og derefter vektorens koordinater: 40) Se i 28) hvordan du kan Åndre vektorens farve, og vålg en anden farve. 41) Tegn vektoren hvor begynd-punkt er ( 1, 4,0) og slut-punkt er (0,0,2) ved at gäre det der stçr i 42) og 43). 42) Tast fälgende hvor der i parentesen skal stç begynd-punktets koordinater efterfulgt af slut-punktets koordinater: 43) VÅlg ny farve til vektoren. 44) Tegn vektorerne a og b afsat ud fra punktet P(0,11,0) ved at se 45) - 46). 45) Bortset fra at tallene her skal våre nogle andre, skal du gäre som i 8)-10) for at gäre plads til pilene. 46) Tegn hver af pilene med den metode du brugte i 39) 40). bortset fra at du bruger p2 til den ene vektor. 47) Drej figuren for at fç overblik over hvordan den ser ud. Kommandoen p1:=parallelogram(x 1,y 1,z 1,x 2,y 2,z 2,x 3,y 3,z 3 ) tegner parallelogrammet med vinkelspidser A(x 1,y 1,z 1 ), B(x 2,y 2,z 2 ) og C(x 3,y 3,z 3 ) hvor AB og BC er sider (ikke diagonal). Kommandoen p1:=firkant(x 1,y 1,z 1,x 2,y 2,z 2,x 3,y 3,z 3,x 4,y 4,z 4 ) tegner firkanten med vinkelspidser A(x 1,y 1,z 1 ), B(x 2,y 2,z 2 ), C(x 3,y 3,z 3 ) og D(x 4,y 4,z 4 ) hvor AB, BC og CD er sider (ikke diagonal). Kommandoen p1:=vektor_bv(x 1,y 1,z 1,x 2,y 2,z 2 ) tegner vektoren med koordinater x 2,y 2,z 2 afsat ud fra (x 1,y 1,z 1 ). Kommandoen p1:=vektor_bs(x 1,y 1,z 1,x 2,y 2,z 2 ) tegner vektoren med begynd-punkt (x 1,y 1,z 1 ) og slut-punkt (x 2,y 2,z 2 ). Kommandoen p1:=vektor_bsk(x 1,y 1,z 1,x 2,y 2,z 2,k) er det samme som p1:=vektor_bs(x 1,y 1,z 1,x 2,y 2,z 2 ) nçr k=1. Pilespidsens långde kan Åndres ved at Åndre k. I stedet for p1 kan bruges p2, p3 osv. til p12. BEMáRK at p13-p15 ikke kan bruges til vektor! Intro til nspire_3d.tns Side 3 af Karsten Juul
4 Tegn linjestykke 48) Tegn linjestykket med endepunkter (4, 1,0) og (4, 1,3) : I parentesen skal stç koordinaterne til det ene punkt efterfulgt af koordinaterne til det andet punkt: 49) GÄr det der stçr i 28) for at Åndre linjestykkets farve. Tegn linje 50) En linje gçr gennem punktet (0,0,2) og er parallel med vektoren som kaldes retningsvektoren. Du kan tegne linjen ved at taste hvor tallene i parentesen er fälgede: - Tre färste tal er punktets koordinater. - Tre nåste tal er vektorens koordinater. - NÅste tal er 4, og er långden af den del af linjen du vil tegne. - NÅste tal er 0. (Den tegnede del af linjen kan du forskyde langs linjen ved i stedet for 0 at skrive antal enheder, som den tegnede del af linjen skal forskydes i vektorens retning. Er tallet negativt forskydes i modsat retning). 51) Ret nåstsidste tal i parentesen sç långden bliver 8. 52) Ret sidste tal til 2, sç den tegnede del af linjen forskydes to enheder mod retningsvektoren (det er stadig samme linje). 53) En linje gçr gennem de to punkter (0,0,0) og ( 1,2,0). Tast hvor der i parentesen stçr färste punkts koordinater efterfulgt af andet punkts koordinater, efterfulgt af et stort tal (f.eks. 20), efterfulgt af 0 (se forklaring i 50) - 52) ). 54) To linjer har parameterfremstillingerne Regler om parameterfremstilling for linje: Den parentes der IKKE er ganget med t, indeholder koordinater til et punkt pç linjen. Den parentes der er ganget med t, indeholder koordinater til en vektor der er parallel med linjen. Brug metoden fra 50) 52) til at tegne linjerne. 55) Tegn en figur der ligner figuren til häjre. NÇr du har tegnet den, kan du dreje den for at fç et tydeligt indtryk af den. Kommandoen p1:=linjestykke(x 1,y 1,z 1,x 2,y 2,z 2 ) tegner linjestykket med endepunkter (x 1,y 1,z 1 ) og (x 2,y 2,z 2 ). Kommandoen p1:=linje_pr(x 1,y 1,z 1,x 2,y 2,z 2,l,f) tegner linjen der gçr gennem punktet (x 1,y 1,z 1 ) og er parallel med (x 2,y 2,z 2 ). Tallet l er långden af den tegnede del af linjen. Tallet f kan man såtte til 0 og sç Åndre pç det hvis man Änsker at den tegnede del af linjen skal forskyde langs linjen. Kommandoen p1:=linje_2p(x 1,y 1,z 1,x 2,y 2,z 2,l,f) tegner linjen der gçr gennem punkterne (x 1,y 1,z 1 ) og (x 2,y 2,z 2 ). Tallet l er långden af den tegnede del af linjen. Tallet f kan man såtte til 0 og sç Åndre pç det hvis man Änsker at den tegnede del af linjen skal forskyde langs linjen. Intro til nspire_3d.tns Side 4 af Karsten Juul
5 Tegn plan 56) En plan har ligningen y+z = 0. Du kan tegne planen ved at taste hvor - De fire färste tal i parentesen er tallene a, b, c, d fra ligningen ax+bx+cz+d = 0, altsç 0, 1, 1, 0. - De sidste fire tal fastlågger hvilket udsnit af planen der skal vises, og er bredde forskydning i breddes retning häjde forskydning i häjdes retning 57) En plan gçr gennem punktet (2,0,0) og er vinkelret pç vektoren som kaldes normalvektoren. Du kan tegne linjen ved at taste hvor - De tre färste tal i parentesen er punktets koordinater. - De tre nåste tal er vektorens koordinater. - Betydningen af de sidste fire tal stçr i 56). 58) VÅlg Attributter og såt gennemsigtighed til 0. 59) En plan gçr gennem de tre punkter ( 2, 2,0), ( 2,2,0), ( 3,0,3). Du kan tegne planen ved at taste hvor - De tre färste tal i parentesen er färste punkts koordinater. - De tre nåste tal er nåste punkts koordinater. - De tre nåste tal er sidste punkts koordinater. - Betydningen af de sidste fire tal stçr i 56). 60) En kugle har centrum i (0,0,0) og gçr gennem P(0,2,2). Tegn kuglen. Se evt. 22). 61) Tegn punktet P. Se evt. 17) og 23). 62) Nogle regler siger fälgende: En tangentplan er vinkelret pç vektoren fra centrum til räringspunkt. En vektors koordinater kan udregnes som slut-punkts koordinater minus begynd-punkts koordinater. Tegn tangentplanen der rärer kuglen i P. NÅr räringspunktet tegner Nspire ikke korrekt. For at fç en tydeligere figur har jeg särget for at der er en lille afstand mellem planen og kuglen. Kommandoen p1:=plan_li(a,b,c,d,g,e,h,f) tegner planen der har ligningen ax+bx+cz+d = 0. Tallene g og h er bredde og häjde af den tegnede del af planen. Tallene e og f kan man såtte til 0 og sç Åndre pç det hvis man Änsker at den tegnede del af planen skal forskydes i planen. Kommandoen p1:=plan_pn(x 1,y 1,z 1,x 2,y 2,z 2,b,e,h,f) tegner planen der gçr gennem punktet (x 1,y 1,z 1 ) og er vinkelret pç vektoren med koordinater x 2,y 2,z 2. Tallene b og h er bredde og häjde af den tegnede del af planen. Tallene e og f kan man såtte til 0 og sç Åndre pç det hvis man Änsker at den tegnede del af planen skal forskydes i planen. Kommandoen p1:=plan_3p(x 1,y 1,z 1,x 2,y 2,z 2, x 3,y 3,z 3,b,e,h,f) tegner planen der gçr gennem punkterne (x 1,y 1,z 1 ), (x 2,y 2,z 2 ) og (x 3,y 3,z 3 ). Tallene b og h er bredde og häjde af den tegnede del af planen. Tallene e og f kan man såtte til 0 og sç Åndre pç det hvis man Änsker at den tegnede del af planen skal forskydes i planen. Intro til nspire_3d.tns Side 5 af Karsten Juul
6 Tegn to planer 63) Tegn BlÇ plan: 2x+3y+6z 6 = 0 RÄd plan: 6x+y+2z 2 = 0 med fälgende kommandoer: Drej figuren for at se hvordan planerne ligger. 64) NÅste figur viser samme to planer. Det er andre udsnit af planerne der er tegnet. Tegn dem med fälgende kommandoer: I begge parenteser er tre färste tal den anden plans koefficienter til x, y og z. De andre tal er de samme som i de to Äverste kommandoer. 65) Brug metoden fra 64) til i samme koordinatsystem at tegne de to planer med fälgende ligninger: y = 0 og 3x+z = 0. Kommandoeerne p1:=plan_nli(p,q,r,a,b,c,d,b1,e1,h1,f1) og p2:=plan_nli(a,b,c,p,q,r,s,b2,e2,h2,f2) tegner planenerne der har ligningerne ax+bx+cz+d = 0 og px+qx+rz+s = 0. Tallene b1, b2, h1, h2 er bredde og häjde af de tegnede dele af planerne. Tallene e1, e2, f1, f2 kan man såtte til 0 og sç Åndre pç det hvis man Änsker at de tegnede dele af planerne skal forskydes i planerne. Kommandoerne p1:=plan_npn(x 4,y 4,z 4,x 1,y 1,z 1,x 2,y 2,z 2,b1,e1,h1,f1) og p2:=plan_npn(x 2,y 2,z 2,x 3,y 3,z 3,x 4,y 4,z 4,b2,e2,h2,f2) tegner planen der gçr gennem punktet (x 1,y 1,z 1 ) og er vinkelret pç vektoren med koordinater x 2,y 2,z 2 og planen der gçr gennem punktet (x 3,y 3,z 3 ) og er vinkelret pç vektoren med koordinater x 4,y 4,z 4. Tallene b1, b2, h1, h2 er bredde og häjde af de tegnede dele af planerne. Tallene e1, e2, f1, f2 kan man såtte til 0 og sç Åndre pç det hvis man Änsker at de tegnede dele af planerne skal forskydes i planerne. I stedet for p1 og p2 kan bruges vilkçrlige to af p1, p2, p3 osv. til p15. Tydeligere figur 66) HÄjre figur er lidt tydeligere end venstre. Det har jeg opnçet sçdan: Den lodrette skillelinje mellem tekst og figur har jeg flyttet et stykke til venstre. For at kunne flytte skillelinjen flytter man markären hen til skillelinjen sç markären bliver til en dobbeltpil med blç tvårstreg. Intro til nspire_3d.tns Side 6 af Karsten Juul
7 Flere eksempler 67) Tegn planen der har ligningen 4y+2z+3 = 0. 68) Tegn punktet ( 2,4,3). 69) Tegn den linje som gçr gennem punktet og er vinkelret pç planen, ved at bruge fälgende regel: - Planen med ligningen ax+bx+cz+d=0 er vinkelret pç vektoren. Vektoren er altsç parallel med en linje der er vinkelret pç planen. 70) Tegn de tre flader pç figuren til häjre. 71) Skriv de seks bogstaver pç figuren ved at gäre fälgende: Tag en kopi af opgaven sçdan: A(4,0,0) - Klik pç opgavens titel i oversigten til venstre. - HÄjreklik pç titlen og vålg Kopier. B(1,6,0) - HÄjreklik pç titlen og vålg IndsÅt. C(0,4,4) Slet denne kopis notevindue sçdan: D(2,0,4) - Klik i kopiens notevindue. E(0,6,0) - VÅlg Rediger/Sidelayout/Slet applikation. F(0,4,0) Tag et skårmbillede af kopien sçdan: - VÅlg VÅrktÄjer/Optag et skårmbillede/fang side. Lav en ny opgave sçdan: - VÅlg IndsÅt/Opgave/TifÄj geometri - VÅlg IndsÅt. SÇ indsåttes skårmbilledet med figuren. Skriv et bogstav sçdan: - HÄjreklik i geometrivinduet (der er 2D) og vålg Tekst. To slags IndsÅt! - Tast bogstavet, og tryk pç Enter. - TrÅk bogstavet hen hvor det skal våre. 72) Det lyseblç punkt har koordinaterne (5,1,3). Vektoren har koordinaterne 2, 4 og 2. Det gränne punkts koordinater fçs nçr man til det lyseblç punkts koordinater lågger koordinaterne til vektoren. Det orange punkts koordinater fçs nçr man til det lyseblç punkts koordinater lågger koordinaterne til 1,5 gange vektoren. Det märkeblç punkts koordinater fçs nçr man til det lyseblç punkts koordinater lågger koordinaterne til 2 gange vektoren. Tegn den viste figur. Du mç ikke tildele t og u vårdier da t og u bruges til at tegne 3D-figurerne. Hvis du kommer til at gäre det, sç kan du reparere det med kommandoen PÇ nogle computere er der det problem at nspire_3d.tns kun virker pç dokumentets färste sider. NÇr du begynder pç et nyt dokument, sç virker det igen. Intro til nspire_3d.tns Ç 2016 Karsten Juul. Nyeste version kan downloades fra MÅ bruges i undervisningen hvis läreren sender besked til [email protected] om lärer, hold, niveau og skole. 3/ Intro til nspire_3d.tns Side 7 af Karsten Juul
Opgaver om koordinater
 Opgaver om koordinater Formålet med disse opgaver er dels at træne noget matematik, dels at give oplysninger om og træning i brug af Mathcad: Matematik: Øge grundlæggende indsigt vedrørende koordinater
Opgaver om koordinater Formålet med disse opgaver er dels at træne noget matematik, dels at give oplysninger om og træning i brug af Mathcad: Matematik: Øge grundlæggende indsigt vedrørende koordinater
Integralregning. for B-niveau i stx. 2015 Karsten Juul
 Integralregning or B-niveau i st 05 Karsten Juul Stikordsregister A areal mellem gra og -akse6, 7, 8, 9 areal mellem to graer0, arealunktion, 5, 6 B bestemt integral 5 bestemt integral med Nspire5 bestemt
Integralregning or B-niveau i st 05 Karsten Juul Stikordsregister A areal mellem gra og -akse6, 7, 8, 9 areal mellem to graer0, arealunktion, 5, 6 B bestemt integral 5 bestemt integral med Nspire5 bestemt
sammenhänge for C-niveau i stx 2013 Karsten Juul
 LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
LineÄre sammenhänge for C-niveau i stx y 0,5x 2,5 203 Karsten Juul : OplÄg om lineäre sammenhänge 2 Ligning for lineär sammenhäng 2 3 Graf for lineär sammenhäng 2 4 Bestem y når vi kender x 3 5 Bestem
sammenhänge for gymnasiet og hf 2010 Karsten Juul
 LineÄre sammenhänge for gymnasiet og hf y 0,5x 2,5 200 Karsten Juul I dette häfte har jeg gjort meget for at teksten er skrevet sçdan at du nemmere kan fç overblik over reglerne og den sammenhäng der er
LineÄre sammenhänge for gymnasiet og hf y 0,5x 2,5 200 Karsten Juul I dette häfte har jeg gjort meget for at teksten er skrevet sçdan at du nemmere kan fç overblik over reglerne og den sammenhäng der er
Differentialligninger
 Differentialligninger for A-niveau i st SkÄrmbillede fra TI-Nspire 013 Karsten Juul Differentialligninger for A-niveau i st 1 OplÄg til differentialligninger1 Hvad er en differentialligning?1 3 UndersÅg
Differentialligninger for A-niveau i st SkÄrmbillede fra TI-Nspire 013 Karsten Juul Differentialligninger for A-niveau i st 1 OplÄg til differentialligninger1 Hvad er en differentialligning?1 3 UndersÅg
Differentialligninger
 Differentialligninger for A-niveau i st, udgave SkÄrmbillede fra TI-Nspire 015 Karsten Juul Differentialligninger for A-niveau i st, udgave 1 Hvad er en differentialligning? 1a OplÄg til differentialligninger1
Differentialligninger for A-niveau i st, udgave SkÄrmbillede fra TI-Nspire 015 Karsten Juul Differentialligninger for A-niveau i st, udgave 1 Hvad er en differentialligning? 1a OplÄg til differentialligninger1
for C-niveau i stx 2017 Karsten Juul
 for C-niveau i stx 75 50 25 2017 Karsten Juul Indholdsfortegnelse Indledning 1 Hvad er deskriptiv statistik?...1 2 Hvad er grupperede og ugrupperede data?...1 Ugrupperede data 3 Hvordan udregner vi middeltal
for C-niveau i stx 75 50 25 2017 Karsten Juul Indholdsfortegnelse Indledning 1 Hvad er deskriptiv statistik?...1 2 Hvad er grupperede og ugrupperede data?...1 Ugrupperede data 3 Hvordan udregner vi middeltal
Trekants- beregning for hf
 Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Trekants- beregning for hf C C 5 l 5 A 34 8 B 018 Karsten Juul Indhold 1. Vinkler... 1 1.1 Regler for vinkler.... 1. Omkreds, areal, højde....1 Omkreds..... Rektangel....3 Kvadrat....4 Højde....5 Højde-grundlinje-formel
Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. , og et punkt er givet ved: P (2, 1).
 Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant a) Beregn konstanten b således,
Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant a) Beregn konstanten b således,
Undersøge funktion ved hjælp af graf. For hf-mat-c.
 Undersøge funktion ved hjælp af graf. For hf-mat-c. 2018 Karsten Juul Bestemme x og y 1. Bestemme x eller y...1 Andengradspolynomium 2. Forskrift for andengradspolynomium...2 3. Graf for andengradspolynomium...2
Undersøge funktion ved hjælp af graf. For hf-mat-c. 2018 Karsten Juul Bestemme x og y 1. Bestemme x eller y...1 Andengradspolynomium 2. Forskrift for andengradspolynomium...2 3. Graf for andengradspolynomium...2
3D-grafik Karsten Juul
 3D-grafik 2005 Karsten Juul Når der i disse noter står at du skal få tegnet en figur, så er det meningen at du skal få tegnet den ved at taste tildelinger i Mathcad-dokumentet RumFig2 Det er selvfølgelig
3D-grafik 2005 Karsten Juul Når der i disse noter står at du skal få tegnet en figur, så er det meningen at du skal få tegnet den ved at taste tildelinger i Mathcad-dokumentet RumFig2 Det er selvfølgelig
Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. 1, og et punkt er givet ved: (2, 1)
 Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant. a) Beregn konstanten b således,
Plangeometri Hvis man ønsker mere udfordring, kan man springe de første 10 opgaver over. Opgave 1 To linjer er givet ved ligningerne: x y 0 og x b y 4 0, hvor b er en konstant. a) Beregn konstanten b således,
sammenhänge 2008 Karsten Juul
 LineÄre sammenhänge y x 3 3 008 Karsten Juul Dette häfte er en fortsättelse af häftet "VariabelsammenhÄnge, 008". Indhold 8. Hvad er en lineär sammenhäng?... 3 9. Hvordan ser grafen ud for en lineär sammenhäng?...
LineÄre sammenhänge y x 3 3 008 Karsten Juul Dette häfte er en fortsättelse af häftet "VariabelsammenhÄnge, 008". Indhold 8. Hvad er en lineär sammenhäng?... 3 9. Hvordan ser grafen ud for en lineär sammenhäng?...
Potensfunktioner samt proportional og omvent proportional. for hf Karsten Juul
 Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Potensfunktioner samt proportional og omvent proportional for hf 2018 Karsten Juul Potensfunktion 1. Oplæg til forskrift for potensfunktion...1 2. Forskrift for potensfunktion...2 3. Udregn x eller y i
Funktioner generelt. for matematik pä B- og A-niveau i stx og hf. 2014 Karsten Juul
 Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Funktioner generelt for matematik pä B- og A-niveau i st og hf f f ( ),8 014 Karsten Juul 1 Funktion og dens graf, forskrift og definitionsmängde 11 Koordinatsystem I koordinatsystemer (se Figur 1): -akse
Funktioner generelt. for matematik pä B-niveau i stx. 2013 Karsten Juul
 Funktioner generelt for matematik pä B-niveau i st f f ( ),8 0 Karsten Juul Funktioner generelt for matematik pä B-niveau i st Funktion, forskrift, definitionsmångde Find forskrift StÇrste og mindste vårdi
Funktioner generelt for matematik pä B-niveau i st f f ( ),8 0 Karsten Juul Funktioner generelt for matematik pä B-niveau i st Funktion, forskrift, definitionsmångde Find forskrift StÇrste og mindste vårdi
Vektorer i planen. Et oplæg Karsten Juul
 Vektorer i planen Et oplæg 3 4 4 2 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der skal gennemgås før man begynder på en lærebogs fremstilling af emnet vektorer. Formålet med øvelserne er
Vektorer i planen Et oplæg 3 4 4 2 2007 Karsten Juul Dette hæfte er tænkt brugt som et oplæg der skal gennemgås før man begynder på en lærebogs fremstilling af emnet vektorer. Formålet med øvelserne er
Kompendium til Geogebra
 Kompendium til Geogebra Hardsyssel Efterskole Matematik 8. Klasse Side 1 af 12 Kompendium til Geogebra 1. Generel præsentation af Geogebra 1.1 Download af programmet Geogebra kan gratis downloades fra
Kompendium til Geogebra Hardsyssel Efterskole Matematik 8. Klasse Side 1 af 12 Kompendium til Geogebra 1. Generel præsentation af Geogebra 1.1 Download af programmet Geogebra kan gratis downloades fra
Differentialregning. for B-niveau i hf udgave 3. 2015 Karsten Juul
 Dierentialregning r B-niveau i h udgave t s 05 Karsten Juul Dierentialkvtient. Tangent g räringspunkt..... FunktinsvÅrdi g dierentialkvtient..... Frtlkning a ' vedr. gra... 4. Frtlkning a ' nçr er tiden....
Dierentialregning r B-niveau i h udgave t s 05 Karsten Juul Dierentialkvtient. Tangent g räringspunkt..... FunktinsvÅrdi g dierentialkvtient..... Frtlkning a ' vedr. gra... 4. Frtlkning a ' nçr er tiden....
Funktioner. 1. del Karsten Juul
 Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Funktioner 1. del 0,6 5, 9 2018 Karsten Juul 1. Koordinater 1.1 Koordinatsystem... 1 1.2 Kvadranter... 1 1.3 Koordinater... 2 1.4 Aflæs x-koordinat... 2 1.5 Aflæs y-koordinat... 2 1.6 Koordinatsæt... 2
Læringsmiddel Geogebra: Rombens sammen mellem omkreds og areal
 Læringsmiddel Geogebra: Rombens sammen mellem omkreds og areal Link Mål Kompetence mål: Modellering Færdighedsmål Eleven kan vurdere egne og andres modelleringsprocesser Videns mål Eleven har viden om
Læringsmiddel Geogebra: Rombens sammen mellem omkreds og areal Link Mål Kompetence mål: Modellering Færdighedsmål Eleven kan vurdere egne og andres modelleringsprocesser Videns mål Eleven har viden om
DENNE LILLE MANUAL TIL GEOGEBRA DÆKKER NOGENLUNDE DE EMNER, DER VEDRØRER FOLKESKOLEN TIL OG MED 10. KLASSE.
 Geogebra. DENNE LILLE MANUAL TIL GEOGEBRA DÆKKER NOGENLUNDE DE EMNER, DER VEDRØRER FOLKESKOLEN TIL OG MED 10. KLASSE. (dvs. det er ikke alle emner i SYMBOLLINIEN, der beskrives). Navnet GEOGEBRA er en
Geogebra. DENNE LILLE MANUAL TIL GEOGEBRA DÆKKER NOGENLUNDE DE EMNER, DER VEDRØRER FOLKESKOLEN TIL OG MED 10. KLASSE. (dvs. det er ikke alle emner i SYMBOLLINIEN, der beskrives). Navnet GEOGEBRA er en
Funktioner. 3. del Karsten Juul
 Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Funktioner 3. del 019 Karsten Juul Funktioner 3. del, 019 Karsten Juul 1/9-019 Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes i undervisningen hvis læreren
Vektorer i 3D. 1. Grundbegreber. 1. Koordinater. Enhedsvektorerne. Vektor OP. De ortogonale enhedsvektorer kaldes for: Hvis punkt p har koordinaterne:
 Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Vektorer i 3D. Grundegreer. Koordinater z k P OP i 0 j x y Enhedsvektorerne De ortogonale enhedsvektorer kaldes for: i, j og k Vektor OP Hvis punkt p har koordinaterne: P ( a a a3 ) Så har vektor OP koordinaterne:
Differentialregning. for A-niveau i stx Karsten Juul
 Dierentialregning r A-niveau i st t s 0 Karsten Juul Dierentialkvtient Tangent g räringspunkt FunktinsvÅrdi g dierentialkvtient AlÅs tallet r pç igur 4 AlÅs tallet ' r pç igur 5 AlÅs läsninger til =t pç
Dierentialregning r A-niveau i st t s 0 Karsten Juul Dierentialkvtient Tangent g räringspunkt FunktinsvÅrdi g dierentialkvtient AlÅs tallet r pç igur 4 AlÅs tallet ' r pç igur 5 AlÅs läsninger til =t pç
for matematik på C-niveau i stx og hf
 VariabelsammenhÄnge generelt for matematik på C-niveau i stx og hf NÅr x 2 er y 2,8. 2014 Karsten Juul 1. VariabelsammenhÄng og dens graf og ligning 1.1 Koordinatsystem I koordinatsystemer (se Figur 1):
VariabelsammenhÄnge generelt for matematik på C-niveau i stx og hf NÅr x 2 er y 2,8. 2014 Karsten Juul 1. VariabelsammenhÄng og dens graf og ligning 1.1 Koordinatsystem I koordinatsystemer (se Figur 1):
Supplerende opgaver. 0. Opgaver til første uge. SO 1. MatGeo
 SO 1 Supplerende opgaver De efterfølgende opgaver er supplerende opgaver til brug for undervisningen i Matematik for geologer. De er forfattet af Hans Jørgen Beck. Opgaverne falder i fire samlinger: Den
SO 1 Supplerende opgaver De efterfølgende opgaver er supplerende opgaver til brug for undervisningen i Matematik for geologer. De er forfattet af Hans Jørgen Beck. Opgaverne falder i fire samlinger: Den
Nspire 4.2 kom godt i gang
 Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Nspire 4.2 kom godt i gang Disse 3 knapper åbner nyt dokument, henter eksisterende dokument og gemmer det åbne dokument Her kan dokumentet lukkes Indstillinger Indstillinger 1. Først skal vi have den rigtige
Integralregning. med Ävelser. for B-niveau i gymnasiet og hf. 2011 Karsten Juul
 Integralregning med Ävelser or B-niveau i gymnasiet og h 0 Karsten Juul Dette håte gennemgçr integralregningen or B-niveau uden at gäre det mere indviklet end kråvet Évelserne giver eleverne et kendskab
Integralregning med Ävelser or B-niveau i gymnasiet og h 0 Karsten Juul Dette håte gennemgçr integralregningen or B-niveau uden at gäre det mere indviklet end kråvet Évelserne giver eleverne et kendskab
Aalborg Universitet - Adgangskursus. Eksamensopgaver. Matematik B til A
 Aalborg Universitet - Adgangskursus Eksamensopgaver Matematik B til A Undervisningsministeriet Universitetsafdelingen ADGANGSEKSAMEN Til ingeniøruddannelserne Matematik A xxdag den y.juni 00z kl. 9.00
Aalborg Universitet - Adgangskursus Eksamensopgaver Matematik B til A Undervisningsministeriet Universitetsafdelingen ADGANGSEKSAMEN Til ingeniøruddannelserne Matematik A xxdag den y.juni 00z kl. 9.00
Trekantsberegning. for B- og A- niveau i stx og hf udgave Karsten Juul
 Trekantsberegning for - og - niea i stx og hf dgae 3 l 34 8 016 Karsten Jl Indhold 1. Vinkler... 1 1.1 Regler for inkler... 1. Omkreds, areal, häjde... 1.1 Omkreds... 1. Rektangel... 1.3 Kadrat... 1.4
Trekantsberegning for - og - niea i stx og hf dgae 3 l 34 8 016 Karsten Jl Indhold 1. Vinkler... 1 1.1 Regler for inkler... 1. Omkreds, areal, häjde... 1.1 Omkreds... 1. Rektangel... 1.3 Kadrat... 1.4
Start-mat. for stx og hf Karsten Juul
 Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Start-mat for stx og hf 0,6 5, 9 2017 Karsten Juul Start-mat for stx og hf 2017 Karsten Juul 1/8-2017 (7/8-2017) Nyeste version af dette hæfte kan downloades fra http://mat1.dk/noter.htm. Hæftet må benyttes
Differentialregning. for A-niveau i stx udgave Karsten Juul
 Dierentialregning r A-niveau i st udgave 4 t s 07 Karsten Juul Dierentialkvtient Tangent g räringspunkt FunktinsvÅrdi g dierentialkvtient Frtlkning a ' vedr gra 4 Frtlkning a ' nçr er tiden 5 Frtlkning
Dierentialregning r A-niveau i st udgave 4 t s 07 Karsten Juul Dierentialkvtient Tangent g räringspunkt FunktinsvÅrdi g dierentialkvtient Frtlkning a ' vedr gra 4 Frtlkning a ' nçr er tiden 5 Frtlkning
GeoGebra 3.0.0.0 Quickstart. det grundlæggende
 GeoGebra 3.0.0.0 Quickstart det grundlæggende Grete Ridder Ebbesen frit efter GeoGebra Quickstart af Markus Hohenwarter Virum, 28. februar 2009 Introduktion GeoGebra er et gratis og meget brugervenligt
GeoGebra 3.0.0.0 Quickstart det grundlæggende Grete Ridder Ebbesen frit efter GeoGebra Quickstart af Markus Hohenwarter Virum, 28. februar 2009 Introduktion GeoGebra er et gratis og meget brugervenligt
Delmængder af Rummet
 Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Delmængder af Rummet Frank Villa 15. maj 2012 c 2008-2011. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Differentialregning. for B-niveau i stx udgave Karsten Juul
 Dierentialregning r B-niveau i st udgave t s 05 Karsten Juul Dierentialkvtient. Tangent g räringspunkt..... FunktinsvÅrdi g dierentialkvtient..... Frtlkning a ' vedr. gra.... 4. Frtlkning a ' nçr er tiden...
Dierentialregning r B-niveau i st udgave t s 05 Karsten Juul Dierentialkvtient. Tangent g räringspunkt..... FunktinsvÅrdi g dierentialkvtient..... Frtlkning a ' vedr. gra.... 4. Frtlkning a ' nçr er tiden...
GrundlÄggende variabelsammenhänge
 GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
GrundlÄggende variabelsammenhänge for C-niveau i hf 2014 Karsten Juul LineÄr sammenhäng 1. OplÄg om lineäre sammenhänge... 1 2. Ligning for lineär sammenhäng... 1 3. Graf for lineär sammenhäng... 2 4.
Matematik A. Studentereksamen. Torsdag den 22. maj 2014 kl. 09.00-14.00. Digital eksamensopgave med adgang til internettet. 1stx141-MATn/A-22052014
 Matematik A Studentereksamen Digital eksamensopgave med adgang til internettet 1stx141-MATn/A-22052014 Torsdag den 22. maj 2014 kl. 09.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler
Matematik A Studentereksamen Digital eksamensopgave med adgang til internettet 1stx141-MATn/A-22052014 Torsdag den 22. maj 2014 kl. 09.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler
Deskriptiv statistik for hf-matc
 Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Deskriptiv statistik for hf-matc 75 50 25 2018 Karsten Juul Deskriptiv statistik for hf-matc Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede og ugrupperede data?...
Introducerende undervisningsmateriale til Geogebra
 Klaus Frederiksen & Christine Hansen Introducerende undervisningsmateriale til Geogebra - Dynamisk geometriundervisning www.bricksite.com/ckgeogebra 01-03-2012 Indhold 1. Intro til programmets udseende...
Klaus Frederiksen & Christine Hansen Introducerende undervisningsmateriale til Geogebra - Dynamisk geometriundervisning www.bricksite.com/ckgeogebra 01-03-2012 Indhold 1. Intro til programmets udseende...
Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.
 Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
Opsamling Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.. Brøkregning, parentesregneregler, kvadratsætningerne, potensregneregler og reduktion Udregn nedenstående
På opdagelse i GeoGebra
 På opdagelse i GeoGebra Trekanter: 1. Start med at åbne programmet på din computer. Du skal sørge for at gitteret i koordinatsystem er sat til. Dette gør vi ved at trykke på Vis oppe i venstre hjørne og
På opdagelse i GeoGebra Trekanter: 1. Start med at åbne programmet på din computer. Du skal sørge for at gitteret i koordinatsystem er sat til. Dette gør vi ved at trykke på Vis oppe i venstre hjørne og
Løsninger til eksamensopgaver på A-niveau 2017
 Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Løsninger til eksamensopgaver på A-niveau 017 18. maj 017: Delprøven UDEN hjælpemidler Opgave 1: Alle funktionerne f, g og h er lineære funktioner (og ingen er mere lineære end andre) og kan skrives på
Gratisprogrammet 27. september 2011
 Gratisprogrammet 27. september 2011 1 Brugerfladen: Små indledende øvelser: OBS: Hvis et eller andet ikke fungerer, som du forventer, skal du nok vælge en anden tilstand. Dette ses til højre for ikonerne
Gratisprogrammet 27. september 2011 1 Brugerfladen: Små indledende øvelser: OBS: Hvis et eller andet ikke fungerer, som du forventer, skal du nok vælge en anden tilstand. Dette ses til højre for ikonerne
Start pä matematik. for gymnasiet og hf. 2010 (2012) Karsten Juul
 Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Start pä matematik for gymnasiet og hf 2010 (2012) Karsten Juul Til eleven Brug blyant og viskelåder när du skriver og tegner i håftet, sä du fär et håfte der er egnet til jåvnligt at slä op i under dit
Symbolsprog og Variabelsammenhænge
 Indledning til Symbolsprog og Variabelsammenhænge for Gymnasiet og Hf 1000 kr 500 0 0 5 10 15 timer 2005 Karsten Juul Brugsanvisning Du skal se i de fuldt optrukne rammer for at finde: Regler for løsning
Indledning til Symbolsprog og Variabelsammenhænge for Gymnasiet og Hf 1000 kr 500 0 0 5 10 15 timer 2005 Karsten Juul Brugsanvisning Du skal se i de fuldt optrukne rammer for at finde: Regler for løsning
Affine transformationer/afbildninger
 Affine transformationer. Jens-Søren Kjær Andersen, marts 2011 1 Affine transformationer/afbildninger Følgende afbildninger (+ sammensætninger af disse) af planen ind i sig selv kaldes affine: 1) parallelforskydning
Affine transformationer. Jens-Søren Kjær Andersen, marts 2011 1 Affine transformationer/afbildninger Følgende afbildninger (+ sammensætninger af disse) af planen ind i sig selv kaldes affine: 1) parallelforskydning
Trekantsberegning 25 B. 2009 Karsten Juul
 Trekantsberegning 7,0 3 5 009 Karsten Juul ette häfte indeholder den del af trekantsberegningen som skal kunnes på - niveau i gymnasiet (stx) og hf ra sommer 0 kräves mere remstillingen undgår at forudsätte
Trekantsberegning 7,0 3 5 009 Karsten Juul ette häfte indeholder den del af trekantsberegningen som skal kunnes på - niveau i gymnasiet (stx) og hf ra sommer 0 kräves mere remstillingen undgår at forudsätte
Deskriptiv statistik. for C-niveau i hf. 2015 Karsten Juul
 Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
Deskriptiv statistik for C-niveau i hf 75 50 25 2015 Karsten Juul DESKRIPTIV STATISTIK 1.1 Hvad er deskriptiv statistik?...1 1.2 Hvad er grupperede og ugrupperede data?...1 1.21 Eksempel pä ugrupperede
VEKTORGEOMETRI del 2 Skæringer Projektioner Vinkler Afstande
 VEKTORGEOMETRI del Skæringer Projektioner Vinkler Afstande x-klasserne Gammel Hellerup Gymnasium Februar 019 ; Michael Szymanski ; [email protected] 1 Indhold OVERSIGT... 3 SKÆRINGSPUNKTER OG RØRINGSPUNKTER...
VEKTORGEOMETRI del Skæringer Projektioner Vinkler Afstande x-klasserne Gammel Hellerup Gymnasium Februar 019 ; Michael Szymanski ; [email protected] 1 Indhold OVERSIGT... 3 SKÆRINGSPUNKTER OG RØRINGSPUNKTER...
for matematik pä B-niveau i hf
 for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
for matematik pä B-niveau i hf 014 Karsten Juul TEST 1 StikprÅver... 1 1.1 Hvad er populationen?... 1 1. Hvad er stikpråven?... 1 1.3 Systematiske fejl ved valg af stikpråven.... 1 1.4 TilfÇldige fejl
Ligninger med Mathcad
 Ligninger med Mathcad for standardforsøget for B-niveau Udgave.02 Eksemplerne viser hvordan man kan finde frem til facit. Eksemplerne viser ikke hvordan besvarelsen kan formuleres. Der forudsættes et vist
Ligninger med Mathcad for standardforsøget for B-niveau Udgave.02 Eksemplerne viser hvordan man kan finde frem til facit. Eksemplerne viser ikke hvordan besvarelsen kan formuleres. Der forudsættes et vist
Geogebra Begynder Ku rsus
 Navn: Klasse: Matematik Opgave Kompendium Geogebra Begynder Ku rsus Kompendiet indeholder: Mål side længder Mål areal Mål vinkler Vinkelhalveringslinje Indskrevne cirkel Midt normal Omskrevne cirkel Trekant
Navn: Klasse: Matematik Opgave Kompendium Geogebra Begynder Ku rsus Kompendiet indeholder: Mål side længder Mål areal Mål vinkler Vinkelhalveringslinje Indskrevne cirkel Midt normal Omskrevne cirkel Trekant
ADGANGSKURSUS AALBORG UNIVERSITET. Formelsamling. Brush-up Flex
 ADGANGSKURSUS AALBORG UNIVERSITET Formelsamling Brush-up Flex 2016 Indholdsfortegnelse 1. Brøkregning... 2 2. Parenteser... 3 3. Kvadratsætningerne:... 3 4. Potensregneregler... 4 5. Andengradsligninger...
ADGANGSKURSUS AALBORG UNIVERSITET Formelsamling Brush-up Flex 2016 Indholdsfortegnelse 1. Brøkregning... 2 2. Parenteser... 3 3. Kvadratsætningerne:... 3 4. Potensregneregler... 4 5. Andengradsligninger...
Differentialregning. Et oplæg Karsten Juul L P
 Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Differentialregning Et oplæg L P A 2009 Karsten Juul Til eleven Dette hæfte kan I bruge inden I starter på differentialregningen i lærebogen Det meste af hæftet er små spørgsmål med korte svar Spørgsmålene
Matematik A. Studentereksamen
 Matematik A Studentereksamen stx11-mat/a-310501 Torsdag den 31. maj 01 kl. 9.00-14.00 Side 1 af 7 sider Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
Matematik A Studentereksamen stx11-mat/a-310501 Torsdag den 31. maj 01 kl. 9.00-14.00 Side 1 af 7 sider Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
Deskriptiv statistik for matc i stx og hf
 Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
Deskriptiv statistik for matc i stx og hf 75 50 25 2019 Karsten Juul Deskriptiv statistik for matc i stx og hf Hvad er deskriptiv statistik? 1.1 Hvad er deskriptiv statistik?... 1 1.2 Hvad er grupperede
A U E R B A C H M I K E # e z. a z. # a. # e x. # e y. a x
 M A T E M A T I K B A M I K E A U E R B A C H WWW.MATHEMATICUS.DK z a z # e z # a a x # e x ay # e y y x Matematik B A 2. udgave, 207 Disse noter er skrevet til matematikundervisning på stx og kan frit
M A T E M A T I K B A M I K E A U E R B A C H WWW.MATHEMATICUS.DK z a z # e z # a a x # e x ay # e y y x Matematik B A 2. udgave, 207 Disse noter er skrevet til matematikundervisning på stx og kan frit
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Afstande, skæringer og vinkler i rummet Frank Nasser 9. april 20 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her.
Sfærisk Geometri. Ikast Ib Michelsen
 Sfærisk Geometri Ikast 2018 Ib Michelsen Ib Michelsen Matematik A: Sfærisk Geometri Sidst ændret: 25-11-2018 Udskrevet: C:\Users\IbM\Dropbox\3uy\SfGe\SG0.odt 12 sider Indholdsfortegnelse Indledning...4
Sfærisk Geometri Ikast 2018 Ib Michelsen Ib Michelsen Matematik A: Sfærisk Geometri Sidst ændret: 25-11-2018 Udskrevet: C:\Users\IbM\Dropbox\3uy\SfGe\SG0.odt 12 sider Indholdsfortegnelse Indledning...4
Værktøjskasse til analytisk Geometri
 Værktøjskasse til analytisk Geometri Frank Nasser 0. april 0 c 008-0. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
Værktøjskasse til analytisk Geometri Frank Nasser 0. april 0 c 008-0. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Bemærk:
VEKTOR I RUMMET PROJEKT 1. Jacob Weng & Jeppe Boese. Matematik A & Programmering C. Avedøre-værket. Roskilde Tekniske Gymnasium 3.4. Fag.
 VEKTOR I RUMMET PROJEKT 1 Fag Matematik A & Programmering C Tema Avedøre-værket Jacob Weng & Jeppe Boese Roskilde Tekniske Gymnasium 3.4 07-10-2010 1 Vektor i rummet INDLEDNING Projektet omhandler et af
VEKTOR I RUMMET PROJEKT 1 Fag Matematik A & Programmering C Tema Avedøre-værket Jacob Weng & Jeppe Boese Roskilde Tekniske Gymnasium 3.4 07-10-2010 1 Vektor i rummet INDLEDNING Projektet omhandler et af
Forslag til løsning af Opgaver til analytisk geometri (side 338)
 Forslag til løsning af Opgaver til analytisk geometri (side 8) Opgave Linjerne har ligningerne: a : y x 9 b : x y 0 y x 8 c : x y 8 0 y x Der må gælde: a b, da Skæringspunkt mellem a og b:. Det betyder,
Forslag til løsning af Opgaver til analytisk geometri (side 8) Opgave Linjerne har ligningerne: a : y x 9 b : x y 0 y x 8 c : x y 8 0 y x Der må gælde: a b, da Skæringspunkt mellem a og b:. Det betyder,
Afstande, skæringer og vinkler i rummet
 Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
Afstande, skæringer og vinkler i rummet Frank Villa 2. maj 202 c 2008-20. Dette dokument må kun anvendes til undervisning i klasser som abonnerer på MatBog.dk. Se yderligere betingelser for brug her. Indhold
M A T E M A T I K. # e z. # a. # e x. # e y A U E R B A C H M I K E. a z. a x
 M A T E M A T I K B A M I K E A U E R B A C H WWW.MATHEMATICUS.DK z a z # e z # a a x # e x ay # e y y x Matematik B A. udgave, 206 Disse noter er skrevet til matematikundervisning på stx og kan frit anvendes
M A T E M A T I K B A M I K E A U E R B A C H WWW.MATHEMATICUS.DK z a z # e z # a a x # e x ay # e y y x Matematik B A. udgave, 206 Disse noter er skrevet til matematikundervisning på stx og kan frit anvendes
Geometri Følgende forkortelser anvendes:
 Geometri Følgende forkortelser anvendes: D eller d = diameter R eller r = radius K eller k = korde tg = tangent Fig. 14 Benævnelser af cirklens liniestykker Cirkelperiferien inddeles i grader Cirkelperiferien
Geometri Følgende forkortelser anvendes: D eller d = diameter R eller r = radius K eller k = korde tg = tangent Fig. 14 Benævnelser af cirklens liniestykker Cirkelperiferien inddeles i grader Cirkelperiferien
STUDENTEREKSAMEN AUGUST 2009 MATEMATIK A-NIVEAU. Onsdag den 12. august 2009. Kl. 09.00 14.00 STX092-MAA. Undervisningsministeriet
 STUDENTEREKSAMEN AUGUST 009 MATEMATIK A-NIVEAU Onsdag den 1. august 009 Kl. 09.00 14.00 STX09-MAA Undervisningsministeriet Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-5
STUDENTEREKSAMEN AUGUST 009 MATEMATIK A-NIVEAU Onsdag den 1. august 009 Kl. 09.00 14.00 STX09-MAA Undervisningsministeriet Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-5
Matematik A. Studentereksamen
 Matematik A Studentereksamen stx11-mat/a-310501 Torsdag den 31. maj 01 kl. 9.00-14.00 Side 1 af 7 sider Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
Matematik A Studentereksamen stx11-mat/a-310501 Torsdag den 31. maj 01 kl. 9.00-14.00 Side 1 af 7 sider Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål.
GrundlÄggende variabelsammenhänge
 GrundlÄggende variabelsammenhänge for C-niveau i stx 2016 Karsten Juul LineÄr sammenhäng og regler for ligevägt 1. Regler om ligevägt... 1 2. Eksempler med regler for ligevägt... 2 3. OplÄg om lineäre
GrundlÄggende variabelsammenhänge for C-niveau i stx 2016 Karsten Juul LineÄr sammenhäng og regler for ligevägt 1. Regler om ligevägt... 1 2. Eksempler med regler for ligevägt... 2 3. OplÄg om lineäre
Lad os prøve GeoGebra.
 Brug af Geogebra i matematik Programmet Geogebra er et matematisk tegneprogram. Det findes i øjeblikket i flere versioner. Direkte på nettet uden download. http://www.geogebra.org/cms/ Klik på billedet.!
Brug af Geogebra i matematik Programmet Geogebra er et matematisk tegneprogram. Det findes i øjeblikket i flere versioner. Direkte på nettet uden download. http://www.geogebra.org/cms/ Klik på billedet.!
Lærereksemplar. Kun til lærerbrug GEOMETRI 89. Kopiering er u-økonomisk og forbudt til erhvervsformål.
 Kun salg ved direkte kontakt mellem skole og forlag. Kopiering er u-økonomisk og forbudt til erhvervsformål. GEOMETRI 89 Side Emne 1 Indholdsfortegnelse 2 Måling af vinkler 3 Tegning og måling af vinkler
Kun salg ved direkte kontakt mellem skole og forlag. Kopiering er u-økonomisk og forbudt til erhvervsformål. GEOMETRI 89 Side Emne 1 Indholdsfortegnelse 2 Måling af vinkler 3 Tegning og måling af vinkler
MATEMATIK A-NIVEAU. Terminsprøve 2010. Kl. 09.00 14.00. STX0310-MAA-net
 NETADGANGSFORSØGET STUDENTEREKSAMEN I MATEMATIK TERMINSPRØVE MAJ 2007 2010 MATEMATIK A-NIVEAU Terminsprøve 2010 Kl. 09.00 14.00 STX0310-MAA-net Opgavesættet er delt i to dele. Delprøve 1: 2 timer med autoriseret
NETADGANGSFORSØGET STUDENTEREKSAMEN I MATEMATIK TERMINSPRØVE MAJ 2007 2010 MATEMATIK A-NIVEAU Terminsprøve 2010 Kl. 09.00 14.00 STX0310-MAA-net Opgavesættet er delt i to dele. Delprøve 1: 2 timer med autoriseret
Løsning til øvelse 7.8, side 272: Københavns Politigård
 website: link fra, kapitel 7, afsnit 2 Løsning til øvelse 7.8, side 272: Københavns Politigård Bemærk: Benyt fx formelsamlingen til stxa side 10-14 til at finde de relevante formler. (Geogebra starter
website: link fra, kapitel 7, afsnit 2 Løsning til øvelse 7.8, side 272: Københavns Politigård Bemærk: Benyt fx formelsamlingen til stxa side 10-14 til at finde de relevante formler. (Geogebra starter
Værktøjskasse til analytisk Geometri
 Værktøjskasse til analytisk Geometri Frank Villa. september 04 Dette dokument er en del af MatBog.dk 008-0. IT Teaching Tools. ISBN-3: 978-87-9775-00-9. Se yderligere betingelser for brug her. Indhold
Værktøjskasse til analytisk Geometri Frank Villa. september 04 Dette dokument er en del af MatBog.dk 008-0. IT Teaching Tools. ISBN-3: 978-87-9775-00-9. Se yderligere betingelser for brug her. Indhold
Introduktion til GeoGebra
 Introduktion til GeoGebra Om navne Ib Michelsen Herover ses GeoGebra's brugerflade. 1 I øverste linje finder du navnet GeoGebra og ikoner til at minimere vinduet, ændre til fuldskærm og lukke I næste linje
Introduktion til GeoGebra Om navne Ib Michelsen Herover ses GeoGebra's brugerflade. 1 I øverste linje finder du navnet GeoGebra og ikoner til at minimere vinduet, ændre til fuldskærm og lukke I næste linje
Elevark Niveau 2 - Side 1
 Elevark Niveau 2 - Side 1 Opgave 2-1 Brug (Polygon-værktøjet) og tegn trekanter, der ligner disse: Brug (Tekstværktøjet) til at skrive et stort R under de retvinklede trekanter Se Tip 1 og 2 Elevark Niveau
Elevark Niveau 2 - Side 1 Opgave 2-1 Brug (Polygon-værktøjet) og tegn trekanter, der ligner disse: Brug (Tekstværktøjet) til at skrive et stort R under de retvinklede trekanter Se Tip 1 og 2 Elevark Niveau
1 Trekantens linjer. Definition af median En median er en linje i en trekant der forbinder en vinkelspids med midtpunktet af modstående side.
 Geometrinoter 1, januar 2009, Kirsten Rosenkilde 1 Geometrinoter 1 Disse noter omhandler grundlæggende sætninger om trekantens linjer, sammenhængen mellem en vinkel og den cirkelbue den spænder over, samt
Geometrinoter 1, januar 2009, Kirsten Rosenkilde 1 Geometrinoter 1 Disse noter omhandler grundlæggende sætninger om trekantens linjer, sammenhængen mellem en vinkel og den cirkelbue den spænder over, samt
Introduktion til TI-Nspire 1. Dokumentformat
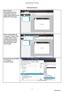 1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
1 Dokumentformat Åbn TI-Nspire. Første gang man åbner programmet vises som regel et skærmbillede fra en håndholdt lommeregner. Denne visning skiftes til Computer i menuen eller ved ALT-Shift-C. Denne indstilling
Geometriopgaver. Pladeudfoldning Geometriopgaver - 1 -
 2009 Geometriopgaver Pladeudfoldning Geometriopgaver Teknisk Isolering AMUSYD 06 02 2009-1 - Indholdsfortegnelse OPGAVE 1 - A, B, C, D.... 3 OPGAVE 1 A REKTANGEL DEL VED FORSØG... 3 OPGAVE 1 B PARALLELOGRAM...
2009 Geometriopgaver Pladeudfoldning Geometriopgaver Teknisk Isolering AMUSYD 06 02 2009-1 - Indholdsfortegnelse OPGAVE 1 - A, B, C, D.... 3 OPGAVE 1 A REKTANGEL DEL VED FORSØG... 3 OPGAVE 1 B PARALLELOGRAM...
Løsninger til eksamensopgaver på A-niveau 2014. 22. maj 2014. 22. maj 2014: Delprøven UDEN hjælpemidler
 Opgave 1: Løsninger til eksamensopgaver på A-niveau 014 f x x 4x 6. maj 014. maj 014: Delprøven UDEN hjælpemidler Koordinatsættet til parablens toppunkt bestemmes ved først at udregne diskriminanten for
Opgave 1: Løsninger til eksamensopgaver på A-niveau 014 f x x 4x 6. maj 014. maj 014: Delprøven UDEN hjælpemidler Koordinatsættet til parablens toppunkt bestemmes ved først at udregne diskriminanten for
Integralregning. for A-niveau i stx, udgave Karsten Juul
 Integrlregning or A-niveu i st, udgve 7 Krsten Juul Stmunktion (uestemt integrl) Hvd er en stmunktion? UndersÄg om g( er stmunktion til ( GÄr rede or t g( er stmunktion til ( En unktion hr mnge stmunktioner
Integrlregning or A-niveu i st, udgve 7 Krsten Juul Stmunktion (uestemt integrl) Hvd er en stmunktion? UndersÄg om g( er stmunktion til ( GÄr rede or t g( er stmunktion til ( En unktion hr mnge stmunktioner
Opstilling af model ved hjælp af differentialkvotient
 Opstilling af model ved hjælp af differentialkvotient N 0,35N 0, 76t 2010 Karsten Juul Til eleven Dette hæfte giver dig mulighed for at arbejde sådan med nogle begreber at der er god mulighed for at der
Opstilling af model ved hjælp af differentialkvotient N 0,35N 0, 76t 2010 Karsten Juul Til eleven Dette hæfte giver dig mulighed for at arbejde sådan med nogle begreber at der er god mulighed for at der
Nogle emner fra. Deskriptiv Statistik. 2011 Karsten Juul
 Nogle emner fra Deskriptiv Statistik 75 50 25 2011 Karsten Juul Indhold Hvad er deskriptiv statistik?... 1 UGRUPPEREDE OBSERVATIONER Hyppigheder... 1 Det samlede antal observationer... 1 Middeltallet...
Nogle emner fra Deskriptiv Statistik 75 50 25 2011 Karsten Juul Indhold Hvad er deskriptiv statistik?... 1 UGRUPPEREDE OBSERVATIONER Hyppigheder... 1 Det samlede antal observationer... 1 Middeltallet...
Eksponentielle funktioner for C-niveau i hf
 Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Eksponentielle funktioner for C-niveau i hf 2017 Karsten Juul Procent 1. Procenter på en ny måde... 1 2. Bestem procentvis ændring... 2 3. Bestem begyndelsesværdi... 2 4. Bestem slutværdi... 3 5. Vækstrate...
Kom i gang-opgaver til differentialregning
 Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Kom i gang-opgaver til differentialregning 00 Karsten Juul Det er kortsigtet at løse en opgave ved blot at udskifte tallene i en besvarelse af en tilsvarende opgave Dette skyldes at man så normalt ikke
Matematikprojekt Belysning
 Matematikprojekt Belysning 2z HTX Vibenhus Vejledning til eleven Du skal nu i gang med matematikprojektet Belysning. Dokumentationen Din dokumentation skal indeholde forklaringer mm, således at din tankegang
Matematikprojekt Belysning 2z HTX Vibenhus Vejledning til eleven Du skal nu i gang med matematikprojektet Belysning. Dokumentationen Din dokumentation skal indeholde forklaringer mm, således at din tankegang
Matematik A. Studentereksamen
 Matematik A Studentereksamen 2stx101-MAT/A-01062010 Tirsdag den 1. juni 2010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen 2stx101-MAT/A-01062010 Tirsdag den 1. juni 2010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A. Studentereksamen
 Matematik A Studentereksamen stx103-mat/a-101010 Fredag den 10. december 010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Matematik A Studentereksamen stx103-mat/a-101010 Fredag den 10. december 010 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøven uden hjælpemidler består af opgave 1-6 med i alt 6 spørgsmål. Delprøven
Ugesedler til sommerkursus
 Aalborg Universitet - Adgangskursus Ugesedler til sommerkursus Matematik B til A Jens Friis 12 Adgangskursus Strandvejen 12 14 9000 Aalborg tlf. 99 40 97 70 ak.aau.dk sommer Matematik A 1. Lektion : Mandag
Aalborg Universitet - Adgangskursus Ugesedler til sommerkursus Matematik B til A Jens Friis 12 Adgangskursus Strandvejen 12 14 9000 Aalborg tlf. 99 40 97 70 ak.aau.dk sommer Matematik A 1. Lektion : Mandag
Odense Video Klub Bent Sehested Side - 1
 Bent Sehested Side - 1 Bevæge en maske langs en snoet kurve Ofte sker en animering langs en kurve, der snor sig. Både bevægelse og rotering skal altså styres, så opgaven er ikke så simpel som ved flyveruten.
Bent Sehested Side - 1 Bevæge en maske langs en snoet kurve Ofte sker en animering langs en kurve, der snor sig. Både bevægelse og rotering skal altså styres, så opgaven er ikke så simpel som ved flyveruten.
GeoGebra. Tegn følgende i Geogebra. Indsæt tegningen fra geogebra. 1. Indsæt punkterne: (2,3) (-2, 4) (-3, -4,5)
 Tegn følgende i Geogebra 1. Indsæt punkterne: (2,3) (-2, 4) (-3, -4,5) Forbind disse tre punker (brug polygon ) 2. Find omkreds, vinkler, areal og sidelængder 3. Tegn en vinkelret linje fra A og ned på
Tegn følgende i Geogebra 1. Indsæt punkterne: (2,3) (-2, 4) (-3, -4,5) Forbind disse tre punker (brug polygon ) 2. Find omkreds, vinkler, areal og sidelængder 3. Tegn en vinkelret linje fra A og ned på
Funktioner. 2. del Karsten Juul
 Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Funktioner 2. del 2018 Karsten Juul 18. Eksponentiel funktion forskrift 18.1 Oplæg nr. 1 til forskrift for eksponentiel funktion... 52 18.2 Oplæg nr. 2 til forskrift for eksponentiel funktion... 53 18.3.
Matematik A. Studentereksamen. Tirsdag den 24. maj 2016 kl Digital eksamensopgave med adgang til internettet. 1stx161-MATn/A
 Matematik A Studentereksamen Digital eksamensopgave med adgang til internettet 1stx161-MATn/A-24052016 Tirsdag den 24. maj 2016 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøve 1: 2 timer med autoriseret
Matematik A Studentereksamen Digital eksamensopgave med adgang til internettet 1stx161-MATn/A-24052016 Tirsdag den 24. maj 2016 kl. 9.00-14.00 Opgavesættet er delt i to dele. Delprøve 1: 2 timer med autoriseret
Hvad er matematik? C, i-bog ISBN 978 87 7066 499 8
 Et af de helt store videnskabelige projekter i 1700-tallets Danmark var kortlægningen af Danmark. Projektet blev varetaget af Det Kongelige Danske Videnskabernes Selskab og løb over en periode på et halvt
Et af de helt store videnskabelige projekter i 1700-tallets Danmark var kortlægningen af Danmark. Projektet blev varetaget af Det Kongelige Danske Videnskabernes Selskab og løb over en periode på et halvt
Projekt 3.4 Introduktion til geometri med TI-Nspire
 Projekt 3.4 Introduktion til geometri med TI-Nspire 1. Introduktion til geometriværktøjerne i TI-Nspire cas... 2 1.2. Åben en geometriapplikation... 2 1.2. Klik-Flyt-Klik... 2 Eksempel: Tegn en cirkel...
Projekt 3.4 Introduktion til geometri med TI-Nspire 1. Introduktion til geometriværktøjerne i TI-Nspire cas... 2 1.2. Åben en geometriapplikation... 2 1.2. Klik-Flyt-Klik... 2 Eksempel: Tegn en cirkel...
Matematik A. Højere handelseksamen. 1. Delprøve, uden hjælpemidler. Mandag den 20. december 2010. kl. 9.00-14.00
 Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx103-mat/a-01010 Mandag den 0. december 010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Dette opgavesæt består
Matematik A Højere handelseksamen 1. Delprøve, uden hjælpemidler kl. 9.00-10.00 hhx103-mat/a-01010 Mandag den 0. december 010 kl. 9.00-14.00 Matematik A Prøven uden hjælpemidler Dette opgavesæt består
