Astrofysik. M bol = konstant + α log Π,
|
|
|
- Victor Østergaard
- 7 år siden
- Visninger:
Transkript
1 Astrofysik Ugeseddel 6 7 9/5 giver jeg en indledning til kosmologi med en gennemgng f Fundmentl Astronomy, Kpitel 19, og det supplerende mterile på denne ugeseddel. 11/5 behndler jeg målinger f kosmologiske prmetre, som behndlet i Ryden, Kpitel 7. Den 16. mj gennemgår jeg observtioner og fortolkning f den kosmiske mikrobølgebggrundsstråling, behndlet i Ryden, Kpitel 9. Jeg foreslår t vi flyser forelæsningen 18. mj (dgen efter Kristi Himmelfrtsdg). Supplerende mterile: Beskrivelsen f kosmologi i Fundmentl Astronomy er lovlig kortfttet, givet feltets voldsomme udvikling i de seneste år. En glimrende introduktion til kosmologi er givet i Brbr Ryden: Introduction to Cosmology (3; Addison Wesley). Jeg vil derfor bruge udvlgte dele f denne bog; det kn vrmt nbefles t nskffe den. På de næste sider f denne ugeseddel giver jeg desuden nogle noter, der udbygger behndlingen f emnerne behndlet i Fundmentl Astronomy og etblerer kontkten til nottionen i Ryden. Ved øvelserne 15. og 16. mj gennemgår vi Opgvesmling til A4 Astrofysik I, Sommereksmen 1987, opgve 1. Antg endvidere t L M 4 for stjerner i ustbilitetsbæltet, og vis t dette giver en reltion på formen M bol = konstnt + α log Π, hvor M bol er den bolometriske størrelsesklsse. Find α og smmenlign med Fundmentl Astronomy, Fig (vi negligerer vritionen i den bolometriske korrektion). Eksmensopgver i Astrofysik, Summer 6, opgve 1. Opgvesmling til A4 Astrofysik I, opgve 46. Eksmensopgver i Astrofysik, Summer 5, opgve. 9. mj 7 Jørgen Christensen-Dlsgrd 1
2 Supplerende noter til kosmologi Topologi og metrik Et fldt to-dimensionlt rum, smt to-dimensionelle rum med positiv og negtiv krumning. Som diskuteret i Fundmentl Astronomy er rummets geometri f stor betydning i kosmologien. Selv om vi der opererer med et fire-dimensionelt rum-tids kontinuum er det nemmere t illustrere geometrien i to dimensioner, som gjort ovenfor. Et mål for en fldes geometri kn fås ud fr vinkelsummen i de illustrerede treknter. I det plne tilfælde gælder selvfølgelig t På en kugleoverflde hr mn t α + β + γ = π. (1) α + β + γ = π + A/R, () hvor A er trekntens rel og R er kuglens rdius. På en mere kompliceret overflde med positiv krumning gælder en tilsvrende reltion, hvor R så beskriver den lokle krumning f flden i det pågældende område. Bemærk t i grænsen R (eller A ) får vi igen ligning (1), som forventeligt. På en overflde med negtiv krumning, som sdlen i figuren, gælder tilsvrende t α + β + γ = π A/R, (3) der igen definerer en lokl krumningsrdius. Geometrien på en overflde er defineret ved metrikken, dvs. fstndsmålet på overflden (se også Appendix B i Fundmentl Astronomy). I et lmindeligt fldt (eller Euklidisk) rum beskrevet i krtesiske koordinter (x, y, z) er et lille fstndselement ds givet ved ds = dx + dy + dz. (4) Bruges i stedet sfærisk polære koordinter (r, θ, φ), hvor θ er vinklen fr polksen, er ds = dr + r (dθ + sin θdφ ) = dr + r dω, (5) Bemærk t overflden til højre på Fig i Fundmentl Astronomy ikke hr meget med en sddel t gøre: den hr negtiv krumning i en retning og positiv krumning i en nden! Fundmentl Astronomy bruger i stedet θ for breddegrden, og hr derfor cos i stedet for sin i deres tilsvrende ligning i Appendix B; den her brugte konvention er den gængse, og er også brugt f Ryden.
3 hvor er et rumvinkelement. I et mere generelt, krumt, rum erstttes dette udtryk med dω = dθ + sin θdφ (6) ds = dr + S κ (r) dω, (7) hvor κ = 1, eller 1 ngiver om rummet hr respektivt positiv krumning, er fldt eller hr negtiv krumning. S κ fhænger f den lokle krumningsrdius R: R sin(r/r) for κ = 1 S κ (r) = r for κ = R sinh(r/r) for κ = 1. Bemærk t for r R er S κ (r) r i lle tilfælde; rummet er ltså loklt fldt. En lterntiv formulering f smmen metrik fås ved t bruge x = S κ (r) som rdil koordint. Så kn ligning (7) skrives ds dx = 1 κx /R + x dω. (9) (Denne nottion er brugt i Fundmentl Astronomy, ligning (19.4), med r i stedet for x.) I speciel reltivitetsteori generliseres den tredimensionelle metrik i det fire-dimensionelle rumtids rum til, f.eks., ds = c dt + dx + dy + dz, (1) hvor c er lyshstigheden og t er tiden; her er rummet stdig fldt. Bemærk t lys udbreder sig lngs en såkldt nul-geodæt, med ds =. I det krumme tilfælde erstttes denne metrik f den såkldte Robertson-Wlker metrik. I det generelle tilfælde, hvor rummets skl er tidsfhængig, og hvor vi ntger homogenitet og isotropi, kn den skrives ds = c dt + (t) [ dr + S κ (r) dω ], (11) hvor (t) er sklfktoren, der ngiver hvor meget de rumlige fstnde hr ændret sig reltivt til en referencetid. Normlt bruges den nuværende tid t = t som reference, (t ) = 1. Så svrer (t) i Fundmentl Astronomy s nottion til R(t)/R. (8) Afstnd og Hubbles lov For t finde fstnden mellem to punkter i rummet (f.eks. en fjern glkse og en igtger på Jorden) til et givet tidspunkt t kn vi lægge koordintsystemet med r = i det ene punkt, og smme θ og φ for de to punkter. Så er fstnden (proper distnce i Ryden) givet ved d p (t) = r ds = (t) dr = (t)r. (1) Herf følger også t ændringen i fstnden per tidsenhed (dvs. hstigheden) er givet ved dd p (t) dt d p (t) = ȧr = ȧ d p(t). (13) 3
4 Specielt på det nuværende tidspunkt hr vi hstigheden v p (t ) = H d p (t ), (14) med H = (ȧ/) t=t, der udtrykker Hubble s lov. Et lterntivt, og meget nyttigt, udtryk for fstnden får vi ved t betrgte en foton udsendt til tiden t = t e fr den fjerne glkse og observeret til tiden t = t. For en foton gælder t ds =, dvs. t cdt = (t)dr. Derfor hr vi t d p (t ) = r t dr = c t e dt (t). (15) Ud fr nlyse f denne reltion kn mn også vise t bølgelængden f lys sklerer som (t): hvis bølgelængden er λ e ved emissionstidspunktet og λ til t = t er λ e (t e ) = λ (t ) ; (16) således er, som nævnt i Fundmentl Astronomy, rødforskydningen z for dette objekt er relteret til (t e ) ved λ = 1 + z = 1 λ e (t e ). (17) En speciel fstnd bseret på ligning (15) får vi ved t betrgte lys udsendt til t = : t d hor (t ) = c dt (t), (18) med (t ) = 1. Lys fr objekter længere væk hr åbenbrt ikke hft tid til t nå os i Universets levetid. Denne fstnd definerer den øjeblikkelige horizont, uden for hvilken der ikke hr kunnet været nogen kommuniktion og dermed vekselvirkning. Friedmnn ligningerne Vi får brug for en lidt mere generel form for Friedmnn ligningerne end givet i Fundmentl Astronomy. Som i udledningen der betrgter vi en Newtonsk pproksimtion, men vi ersttter i ligning (19.3) R 3 ρ med R 3 ρ, ifølge ligning (19.6). Endvidere indfører vi ikke Ω umiddelbrt. Endelig bruger vi = R(t)/R. Resulttet er, t ligning (19.9) kn skrives (ȧ ) = 8πG 3 ρ Λ + C, (19) hvor C er en smlet integrtionskonstnt. Som rgumenteret i Fundmentl Astronomy fås den korrekte reltivistiske form ved t sætte C = κc /R, hvor κ = ( 1,, 1) er krumningskonstnten, og R nu er krumningsrdius til t = t. Altså får vi (ȧ ) = 8πG 3 ρ Λ κc R. () 4
5 Det følger f Einsteins ækvivlens mellem msse og energi t energitætheden bidrger til tyngdefeltet. Således fås den korrekte form ved t ersttte ρ med ɛ/c, hvor ɛ er energitætheden. For lmindeligt stof inkluderer dette hvilemssenenergien, således t vi genfinder et bidrg ρ fr stoffet, hvis dette bevæger sig med hstigheder meget mindre end lyshstigheden. Formelt kn bidrget fr Λ også inkluderes ved t indføre et bidrg ɛ Λ = til ɛ. Dette giver endelig Friedmnn ligningen på formen c 8πG Λ (1) (ȧ ) H(t) = 8πG 3c ɛ κc R, () hvor vi, i nlogi med ligning (14), indførte den øjeblikkelige Hubble prmeter H = ȧ/. Af ligning () følger t fortegnet f κ er defineret f fortegnet f ɛ ɛ c, hvor den kritiske energitæthed er givet ved ɛ c = 3c 8πG H(t). (3) Ofte udtrykker mn energitætheden reltivt til ɛ c, som Ω(t) = ɛ/ɛ c. Som også diskuteret i Fundmentl Astronomy hr rummet positiv krumning, er fldt eller hr negtiv krumning hvis Ω > 1, Ω = 1 eller Ω < 1. Udtrykt ved Ω kn ligning () skrives κc 1 Ω(t) = R (t) H(t). (4) Her er det klrt t højresidens fortegn er konstnt i tiden, og dermed gælder også t Ω enten er < 1, eller > 1 til lle tider. Det relevnte tilfælde kn i princippet fgøres ud fr de nuværende værdier, der giver 1 Ω = κc R. (5) H Den kritiske tæthed i det nuværende Univers kn findes ud fr den målte værdi for Hubblekonstnten, H = 7 km s 1 Mpc 1 ; det giver ɛ c, = 3c 8πG H = J m 3 = 5 MeV m 3. (6) Udtrykt ved den tilsvrende mssetæthed ρ c, = ɛ c, /c fås ρ c, = kg m 3 = M Mpc 3. (7) Vi får også brug for energiligningen for Universet, under ntgelse f en dibtisk proces, uden energiudveksling. Udgngspunktet er gnske simpelt termodynmikkens første hovedsætning for et område V (t), på formen = Q = Ė + P V, (8) hvor Q er hstigheden f vrmetilførsel (= for en dibtisk proces), E er energien i området og P er trykket. Volumen V for et givet område, der udvikler sig med sklfktoren, er proportionlt med (t) 3, så V = 3ȧ V. (9) 5
6 Endvidere hr vi t E = ɛv, og derfor t Ė = ɛv + ɛ V. Alt i lt får vi fr ligning (8) t [ ] V ɛ + 3ȧ (ɛ + P ) =, eller ɛ + 3ȧ (ɛ + P ) =. (3) Denne ligning kn bruges til t udlede en ligning for Universets ccelertion, som vi siden får brug for. Ved t gnge ligning () med og differentiere får vi ȧä = 8πG 3c ( ɛ + ɛȧ). Ved t dividere med ȧ og bruge, ud fr ligning (3), t får vi endelig ccelertionsligningen ɛ ȧ = 3(ɛ + P ), ä = 4πG (ɛ + 3P ) (31) 3c (Ryden, ligning 4.44). For t komme videre hr vi brug for reltioner mellem ɛ og P for de forskellige bestnddele f Universet. Generelt er det bekvemt t skrive sådnne reltioner på formen P = wɛ. (3) For lmindeligt stof (der bevæger sig ikke-reltivistisk) er trykket f smme størrelsesorden som bevægelsesenergien og dermed lngt mindre end hvilemssenergien. Altså er den tilsvrende værdi f w, w m, meget mindre end 1. For stråling (eller ndre ekstremt reltivistiske prtikler) ved vi t w = w rel = 1/3. Endelig kn mn vise t for en simpel konstnt kosmologisk konstnt (hvor også ɛ Λ er konstnt) er w = w Λ = 1. I dette tilfælde hr vi ltså et negtivt tryk (eller en spænding), der bidrger til t ccelerere Universets udvidelse. Bemærk t dette gælder unset t ɛ Λ giver et positivt bidrg til den effektive mssetæhed og dermed til en opbremsning f Universet; men i ligning (31) dominerer bidrget fr P Λ. Hvis de forskellige bidrg til energitætheden ikke vekselvirker, gælder ligning (3) for energitætheden ɛ w for hver komponent seprt. Bruges også ligning (3) hr vi t eller ɛ w ɛ w = 3(1 + w)ȧ, ɛ w = ɛ w, (t) 3(1+w), (33) hvor vi går ud fr t w er konstnt. For lmindeligt stof, med w, hr vi derfor t ɛ = ɛ m = ɛ m, (t) 3. Det følger også f mssebevrelse i et givet område, og f t volumen f området ændrer sig proportionlt med (t) 3. Tilsvrende hr vi for stråling, med w = 1/3, t ɛ = ɛ r = ɛ r, (t) 4. Et simpelt rgument for denne reltion fås ved t benytte t den gennemsnitlige energi f en foton er proportionl med λ 1 (t) 1 (se ligning 16), og t ntlstætheden f fotoner vrierer som (t) 3. Endelig hr vi, for bidrget fr den kosmologiske konstnt, t w = 1 og dermed t ɛ Λ er konstnt, som llerede nført. 6
7 Som vi senere skl se tyder meget på t Universet er fldt, med Ω = 1 og dermed κ =. Hvis en komponent med et givet w dominerer kn vi derfor skrive Friedmnn ligningen som eller og dermed (ȧ ) = 8πG 3c ɛ = 8πG 3c ɛ c, 3(1+w) = H 3(1+w), (34) t (1+3w)/ d = H dt = H t, Endvidere er Universets nuværende lder t (med (t ) = 1) [ ] /(3+3w) 3H (1 + w)t (t) =. (35) t = 3(1 + w) H 1. (36) Dette generliserer udledningen f Fundmentl Astronomy, ligning (19.34). I et Univers domineret f lmindeligt stof, med w, hr vi derfor ( 3H t (t) = ) /3, t = 3 I et Univers domineret f stråling, med w = 1/3, hr vi tilsvrende 1 H. (37) (t) = (H t) 1/, t = 1 H. (38) Som reference bruger Ryden et såkldt Benchmrk Universe ; som vi skl se hr det betydelig støtte observtionelt. Her er Ω = Ω CMB, + Ω m, + Ω Λ, = 1, hvor Ω m, =.3 og Ω Λ,.7. Bidrget Ω CMB, fr den kosmiske bggrundsstråling kn findes ud fr temperturen f strålingen til Ω CMB, = Hertil skl lægges et bidrg fr neutrinoer, der også opfører sig som reltivistiske prtikler. Det smlede strålingsbidrg (eller reltivistiske bidrg) er derfor Ω r, = Alderen f Universet er, med disse prmetre, t = 13.5 Gyr. D Ω m 3 og Ω r 4 er Ω r /Ω m 1. På det nuværende tidspunkt er Universet helt domineret f stof (og Λ) men for < Ω r, /Ω m, dominerede strålingen. Det svrer, i reference-universet, til en lder på år. 7
Benyttede bøger: Introduction to Cosmology, Barbara Ryden, 2003.
 Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Formelsamling Noter til Astronomi 1 You can know the name of a bird in all the languages of the world, but when you re finished, you ll know absolutely nothing whatever about the bird... So let s look
Matematisk modellering og numeriske metoder. Lektion 17
 Mtemtisk modellering og numeriske metoder Lektion 1 Morten Grud Rsmussen 8. november, 1 1 Numerisk integrtion og differentition [Bogens fsnit 19. side 84] 1.1 Grundlæggende om numerisk integrtion Vi vil
Mtemtisk modellering og numeriske metoder Lektion 1 Morten Grud Rsmussen 8. november, 1 1 Numerisk integrtion og differentition [Bogens fsnit 19. side 84] 1.1 Grundlæggende om numerisk integrtion Vi vil
A4: Introduction to Cosmology. Forelæsning 2 (kap. 4-5): Kosmisk Dynamik
 A4: Introduction to Cosmology Forelæsning (kap. 4-5): Kosmisk Dynamik 1-komponent modeller Robertson-Walker metrikken ds = c dt² a t [ Metrik med medfølgende koordinater (x,θ,φ), x= S κ (r) i den rumlige
A4: Introduction to Cosmology Forelæsning (kap. 4-5): Kosmisk Dynamik 1-komponent modeller Robertson-Walker metrikken ds = c dt² a t [ Metrik med medfølgende koordinater (x,θ,φ), x= S κ (r) i den rumlige
Potens regression med TI-Nspire
 Potensvækst og modellering - Mt-B/A 2.b 2007-08 Potens regression med TI-Nspire Vi tger her udgngspunkt i et eksempel med tovværk, hvor mn får oplyst en tbel over smmenhængen mellem dimeteren (xdt) i millimeter
Potensvækst og modellering - Mt-B/A 2.b 2007-08 Potens regression med TI-Nspire Vi tger her udgngspunkt i et eksempel med tovværk, hvor mn får oplyst en tbel over smmenhængen mellem dimeteren (xdt) i millimeter
ANALYSE 1, 2014, Uge 3
 ANALYSE 1, 2014, Uge 3 Forelæsninger Tirsdg. Vi generliserer tlrækker til funktionsrækker ved t udskifte tllene med funktioner (TL Afsnit 12.5). Det svrer til forrige uges skridt fr tlfølger til funktionsfølger.
ANALYSE 1, 2014, Uge 3 Forelæsninger Tirsdg. Vi generliserer tlrækker til funktionsrækker ved t udskifte tllene med funktioner (TL Afsnit 12.5). Det svrer til forrige uges skridt fr tlfølger til funktionsfølger.
ANALYSE 1, 2015, Uge 2
 ANALYSE 1, 2015, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
ANALYSE 1, 2015, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
UGESEDDEL 52. . Dette gøres nedenfor: > a LC
 UGESEDDE 52 Opgve 1 Denne opgve er et mtemtisk eksempel på Ricrdo s én-fktor model, der præsenteres i Krugmn & Obstfeld kpitel 2 side 12-19. Denne model beskriver hndel som et udslg f komprtive fordele
UGESEDDE 52 Opgve 1 Denne opgve er et mtemtisk eksempel på Ricrdo s én-fktor model, der præsenteres i Krugmn & Obstfeld kpitel 2 side 12-19. Denne model beskriver hndel som et udslg f komprtive fordele
Trigonometri. Matematik A niveau
 Trigonometri Mtemtik A niveu Arhus Teh EUX Niels Junge Trigonometri Sinus Cosinus Tngens Her er definitionen for Cosinus Sinus og Tngens Mn kn sige t osinus er den projierede på x-ksen og sinus er den
Trigonometri Mtemtik A niveu Arhus Teh EUX Niels Junge Trigonometri Sinus Cosinus Tngens Her er definitionen for Cosinus Sinus og Tngens Mn kn sige t osinus er den projierede på x-ksen og sinus er den
Erik Vestergaard www.matematikfysik.dk. Erik Vestergaard, 2009.
 Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, 009. Billeder: Forside: Collge f billeder: istock.com/titoslck istock.com/yuri Desuden egne fotos og illustrtioner Erik Vestergrd www.mtemtikfysik.dk
Erik Vestergrd www.mtemtikfysik.dk Erik Vestergrd, 009. Billeder: Forside: Collge f billeder: istock.com/titoslck istock.com/yuri Desuden egne fotos og illustrtioner Erik Vestergrd www.mtemtikfysik.dk
Projekt 5.7 Hovedsætninger om differentiable funktioner et opgaveforløb
 Hvd er mtemtik?, e-og Projekter: Kpitel 5 Projekt 57 Hovedsætninger om differentile funktioner Projekt 57 Hovedsætninger om differentile funktioner et opgveforlø Projektet er en udvidelse f fsnittet i
Hvd er mtemtik?, e-og Projekter: Kpitel 5 Projekt 57 Hovedsætninger om differentile funktioner Projekt 57 Hovedsætninger om differentile funktioner et opgveforlø Projektet er en udvidelse f fsnittet i
Matematik B-A. Trigonometri og Geometri. Niels Junge
 Mtemtik B-A Trigonometri og Geometri Niels Junge Indholdsfortegnelse Indledning...3 Trigonometri...3 Sinusreltionen:...6 Cosinusreltionen...7 Dobbeltydighed...7 Smmendrg...8 Retvinklede treknter...8 Ikke
Mtemtik B-A Trigonometri og Geometri Niels Junge Indholdsfortegnelse Indledning...3 Trigonometri...3 Sinusreltionen:...6 Cosinusreltionen...7 Dobbeltydighed...7 Smmendrg...8 Retvinklede treknter...8 Ikke
gudmandsen.net Geometri C & B
 gudmndsen.net Geometri C & B Indholdsfortegnelse 1 Geometri & trigonometri...2 1.1 Område...2 2 Ensvinklede treknter...3 2.1.1 Skleringsfktoren...4 3 Retvinklede treknter...5 3.1 Pythgors lærersætning...5
gudmndsen.net Geometri C & B Indholdsfortegnelse 1 Geometri & trigonometri...2 1.1 Område...2 2 Ensvinklede treknter...3 2.1.1 Skleringsfktoren...4 3 Retvinklede treknter...5 3.1 Pythgors lærersætning...5
Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen runde
 Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen 016. runde Besvrelser som flder uden for de løsninger som ligger til grund for pointskemerne, bedømmes ved nlogi så skridt med tilsvrende vægt i den
Retningslinjer for bedømmelsen Georg Mohr-Konkurrencen 016. runde Besvrelser som flder uden for de løsninger som ligger til grund for pointskemerne, bedømmes ved nlogi så skridt med tilsvrende vægt i den
Matematisk modellering og numeriske metoder. Lektion 12
 Mtemtisk modellering numeriske metoder Lektion 12 Morten Grud Rsmussen 21. oktober, 213 1 Prtielle differentilligninger 1.1 Løsning f vrmeligningen vh. Fourierrækker [Bens sektion 12.6 på side 558] Vi
Mtemtisk modellering numeriske metoder Lektion 12 Morten Grud Rsmussen 21. oktober, 213 1 Prtielle differentilligninger 1.1 Løsning f vrmeligningen vh. Fourierrækker [Bens sektion 12.6 på side 558] Vi
3. Vilkårlige trekanter
 3. Vilkårlige treknter 3. Vilkårlige treknter I dette fsnit vil vi beskæftige os med treknter, der ikke nødvendigvis er retvinklede. De formler, der er omtlt i fsnittet om retvinklede treknter, kn ikke
3. Vilkårlige treknter 3. Vilkårlige treknter I dette fsnit vil vi beskæftige os med treknter, der ikke nødvendigvis er retvinklede. De formler, der er omtlt i fsnittet om retvinklede treknter, kn ikke
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 39, 009 Produceret f Hns J. Munkholm 1 Linerisering s. 66-67 Lineriseringen f f omkring x =, er den lineære funktion, der hr tngenten som grf. Klder mn den L er forskriften
MM501 forelæsningsslides uge 39, 009 Produceret f Hns J. Munkholm 1 Linerisering s. 66-67 Lineriseringen f f omkring x =, er den lineære funktion, der hr tngenten som grf. Klder mn den L er forskriften
Potens- sammenhænge. inkl. proportionale og omvendt proportionale variable. 2010 Karsten Juul
 Potens- smmenhænge inkl. proportionle og omvendt proportionle vrible 010 Krsten Juul Dette hæfte er en fortsættelse f hæftet "Eksponentielle smmenhænge, udgve ". Indhold 1. Hvd er en potenssmmenhæng?...1.
Potens- smmenhænge inkl. proportionle og omvendt proportionle vrible 010 Krsten Juul Dette hæfte er en fortsættelse f hæftet "Eksponentielle smmenhænge, udgve ". Indhold 1. Hvd er en potenssmmenhæng?...1.
Ny Sigma 9, s Andengradsfunktioner med regneforskrift af typen y = ax + bx + c, hvor a 0.
 Ny Sigm 9, s 110 Andengrdsfunktioner med regneforskrift f typen y = x + x + c, hvor 0 Lineære funktioner (førstegrdsfunktioner) med regneforskrift f typen y = αx + β Grfen for funktioner f disse typer
Ny Sigm 9, s 110 Andengrdsfunktioner med regneforskrift f typen y = x + x + c, hvor 0 Lineære funktioner (førstegrdsfunktioner) med regneforskrift f typen y = αx + β Grfen for funktioner f disse typer
Elementær Matematik. Analytisk geometri
 Elementær Mtemtik Anltisk geometri Ole Witt-Hnsen 0 Indhold. koordintsstemet.... Afstndsformlen.... Liniens ligning...4 4. Ortogonle linier...7 5. Liniers skæring. To ligninger med to uekendte....7 6.
Elementær Mtemtik Anltisk geometri Ole Witt-Hnsen 0 Indhold. koordintsstemet.... Afstndsformlen.... Liniens ligning...4 4. Ortogonle linier...7 5. Liniers skæring. To ligninger med to uekendte....7 6.
Trigonometri. Trigonometri. Sinus og cosinus... 2 Tangens... 6 Opgaver... 9. Side 1
 Trigonometri Sinus og osinus... 2 Tngens... 6 Opgver... 9 Side Sinus og osinus Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus til en vinkel ved t tegne vinklen midt
Trigonometri Sinus og osinus... 2 Tngens... 6 Opgver... 9 Side Sinus og osinus Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus til en vinkel ved t tegne vinklen midt
MM501 forelæsningsslides
 MM501 forelæsningsslides uge 38, 010 Produceret f Hns J. Munkholm berbejdet f Jessic Crter 1 l Hopitls regler Afsnit 4.3 l Hopitls regel I omhndler beregning f grænseværdier f formen lim x f(x) g(x), hvor
MM501 forelæsningsslides uge 38, 010 Produceret f Hns J. Munkholm berbejdet f Jessic Crter 1 l Hopitls regler Afsnit 4.3 l Hopitls regel I omhndler beregning f grænseværdier f formen lim x f(x) g(x), hvor
Noget om Riemann integralet. Noter til Matematik 2
 Noget om Riemnn integrlet. Noter til Mtemtik 2 Arne Jensen Afdeling for Mtemtik og Dtlogi Institut for Elektroniske Systemer Alborg Universitetscenter Fredrik Bjers Vej 7 9220 Alborg Ø 4. pril 1991 Revideret
Noget om Riemnn integrlet. Noter til Mtemtik 2 Arne Jensen Afdeling for Mtemtik og Dtlogi Institut for Elektroniske Systemer Alborg Universitetscenter Fredrik Bjers Vej 7 9220 Alborg Ø 4. pril 1991 Revideret
hvor A er de ydre kræfters arbejde på systemet og Q er varmen tilført fra omgivelserne til systemet.
 !#" $ "&% (')"&*,+.-&/102%435"&6,+879$ *1')*&: or et system, hvor kun den termiske energi ændres, vil tilvæksten E term i den termiske energi være: E term A + Q hvor A er de ydre kræfters rbejde på systemet
!#" $ "&% (')"&*,+.-&/102%435"&6,+879$ *1')*&: or et system, hvor kun den termiske energi ændres, vil tilvæksten E term i den termiske energi være: E term A + Q hvor A er de ydre kræfters rbejde på systemet
Lektion 7s Funktioner - supplerende eksempler
 Lektion 7s Funktioner - supplerende eksempler Oversigt over forskellige tper f funktioner Omvendt proportionlitet og hperler.grdsfunktioner og prler Eksponentilfunktioner Potensfunktioner Lektion 7s Side
Lektion 7s Funktioner - supplerende eksempler Oversigt over forskellige tper f funktioner Omvendt proportionlitet og hperler.grdsfunktioner og prler Eksponentilfunktioner Potensfunktioner Lektion 7s Side
ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG
 ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG INDHOLDSFORTEGNELSE 1 Formelsmling... side 2 Uddbning f visse formler... side 3 2 Grundlæggende færdigheder... side 5 2 Finde konstnterne og b i en formel...
ØVEHÆFTE FOR MATEMATIK C POTENS-SAMMENHÆNG INDHOLDSFORTEGNELSE 1 Formelsmling... side 2 Uddbning f visse formler... side 3 2 Grundlæggende færdigheder... side 5 2 Finde konstnterne og b i en formel...
ANALYSE 1, 2013, Uge 2
 ANALYSE 1, 2013, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
ANALYSE 1, 2013, Uge 2 Forelæsninger Denne uges tem er uendelige rækker. Tirsdg: Tlrækker. En uendelig tlrække består ligesom en uendelig tlfølge f uendelig mnge tl. Forskellen mellem de to begreber består
Det dobbelttydige trekantstilfælde
 Det dobbelttydige trekntstilfælde Heine Strømdhl, Københvns Kommunes Ungdomsskoler Formålet med denne rtikel er t formulere en meget simpel grfisk løsningsmetode til det dobbelttydige trekntstilfælde med
Det dobbelttydige trekntstilfælde Heine Strømdhl, Københvns Kommunes Ungdomsskoler Formålet med denne rtikel er t formulere en meget simpel grfisk løsningsmetode til det dobbelttydige trekntstilfælde med
Michel Mandix (2017) Derfor er der behov for en række værktøjer, som kan bruges også til de vilkårlige trekanter. a b c A B C
 Mihel Mndix (07) Sinusreltionen Nott Side f 9 Sinusreltionen Indtil videre, er der kun eskrevet, hvordn mn eregner på retvinklede treknter. Men desværre er det lngtfr lle treknter, som er retvinklede.
Mihel Mndix (07) Sinusreltionen Nott Side f 9 Sinusreltionen Indtil videre, er der kun eskrevet, hvordn mn eregner på retvinklede treknter. Men desværre er det lngtfr lle treknter, som er retvinklede.
Institut for Matematik, DTU: Gymnasieopgave. Integrationsprincippet og Keplers tønderegel
 Integrtionsprincippet og Keplers tønderegel. side Institut for Mtemtik, DTU: Gymnsieopgve Integrtionsprincippet og Keplers tønderegel Littertur: H. Elrønd Jensen, Mtemtisk nlyse, Institut for Mtemtik,
Integrtionsprincippet og Keplers tønderegel. side Institut for Mtemtik, DTU: Gymnsieopgve Integrtionsprincippet og Keplers tønderegel Littertur: H. Elrønd Jensen, Mtemtisk nlyse, Institut for Mtemtik,
Matematikkens sprog INTRO
 Mtemtikkens sprog Mtemtik hr sit eget sprog, der består f tl og symboler fx regnetegn, brøkstreger bogstver og prenteser På mnge måder er det ret prktisk - det giver fx korte måder t skrive formler på.
Mtemtikkens sprog Mtemtik hr sit eget sprog, der består f tl og symboler fx regnetegn, brøkstreger bogstver og prenteser På mnge måder er det ret prktisk - det giver fx korte måder t skrive formler på.
Om Dido var kyndig i matematik er nok tvivlsomt, men hun havde i hvert fald en veludviklet logisk sans, som vi skal se.
 Forord. Det isoperimetriske problem går i l sin enkelhed ud på t finde den lukkede kurve i plnen, blndt en mængde f kurver lle med smme omkreds, som fgrænser det størst mulige rel. Løsningen til det isoperimetriske
Forord. Det isoperimetriske problem går i l sin enkelhed ud på t finde den lukkede kurve i plnen, blndt en mængde f kurver lle med smme omkreds, som fgrænser det størst mulige rel. Løsningen til det isoperimetriske
Elementær Matematik. Trigonometri
 Elementær Mtemtik Trigonometri Ole Witt-Hnsen 11 Indhold 1. Vinkler...1. Sinus, osinus og tngens...3.1 Overgngsformler...4 3. Den retvinklede treknt...6 4. Den lmindelige treknt. Sinus og osinus reltionerne...8
Elementær Mtemtik Trigonometri Ole Witt-Hnsen 11 Indhold 1. Vinkler...1. Sinus, osinus og tngens...3.1 Overgngsformler...4 3. Den retvinklede treknt...6 4. Den lmindelige treknt. Sinus og osinus reltionerne...8
Eksamensopgave august 2009
 Ib Michelsen, Viborg C / Skive C Side 1 09-04-011 1 Eksmensopgve ugust 009 Opgve 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 Givet ovenstående ensvinklede treknter. D treknterne er ensvinklede, er
Ib Michelsen, Viborg C / Skive C Side 1 09-04-011 1 Eksmensopgve ugust 009 Opgve 1 3 4 5 6 7 8 9 10 11 1 13 14 15 16 17 18 19 0 1 Givet ovenstående ensvinklede treknter. D treknterne er ensvinklede, er
1 1 t 10 1. ( ) x 2 4. + k ================= sin( x) + 4 og har graf gennem (0,2), dvs F(0) = 2. + 4x + k
 0x-MA (0.0.08) _ opg (3:07) Integrtion ved substitution ( x + 7) 9 t x + 7 > t 9 t 0 + k 0 0 ( x + 7)0 + k b) x x + 4 t x + 4 > 3 x t t t x 3 t x x + k 3 t t + k ( ) x 4 3 x + 4 + + k c) cos( x)
0x-MA (0.0.08) _ opg (3:07) Integrtion ved substitution ( x + 7) 9 t x + 7 > t 9 t 0 + k 0 0 ( x + 7)0 + k b) x x + 4 t x + 4 > 3 x t t t x 3 t x x + k 3 t t + k ( ) x 4 3 x + 4 + + k c) cos( x)
Elementær Matematik. Vektorer i planen
 Elementær Mtemtik Vektorer i plnen Køge Gymnsium 0 Ole Witt-Hnsen Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer... 3. Multipliktion f vektor med et tl...3 4. Opløsning
Elementær Mtemtik Vektorer i plnen Køge Gymnsium 0 Ole Witt-Hnsen Indhold. Prllelforskydninger i plnen. Vektorer.... Sum og differens f to vektorer... 3. Multipliktion f vektor med et tl...3 4. Opløsning
Projekt 7.8 To ligninger med to ubekendte
 Projekt 78 To ligninger med to uekendte Den opgve t skulle løse to ligninger med to uekendte er vi stødt på i en række speciltilfælde under ehndlingen f vækstmodellerne: Funktionstype Ligningssystem Lineær
Projekt 78 To ligninger med to uekendte Den opgve t skulle løse to ligninger med to uekendte er vi stødt på i en række speciltilfælde under ehndlingen f vækstmodellerne: Funktionstype Ligningssystem Lineær
MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX)
 Silkeorg -0- MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) FACITLISTE Udrejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger
Silkeorg -0- MATEMATIK-KOMPENDIUM TIL KOMMENDE ELEVER PÅ DE GYMNASIALE UNGDOMSUDDANNELSER I SILKEBORG (HF, HHX, HTX & STX) FACITLISTE Udrejdet f mtemtiklærere fr HF, HHX, HTX & STX. PS: Hvis du opdger
Kort om Potenssammenhænge
 Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
Øvelser til hæftet Kort om Potenssmmenhænge 2011 Krsten Juul Dette hæfte indeholder bl.. mnge småspørgsmål der gør det nemmere for elever t rbejde effektivt på t få kendskb til emnet. Indhold 1. Ligning
KEGLESNIT OG BANEKURVER
 KEGLESNIT OG BANEKURVER x-klsserne Gmmel Hellerup Gymnsium INDHOLDSFORTEGNELSE INDHOLDSFORTEGNELSE... BEGREBET KEGLE... 3 KEGLESNIT... 5 Cirkel... 6 Ellipse... 8 Prbel... 15 Hyperbel... 19 Keglesnitsligninger
KEGLESNIT OG BANEKURVER x-klsserne Gmmel Hellerup Gymnsium INDHOLDSFORTEGNELSE INDHOLDSFORTEGNELSE... BEGREBET KEGLE... 3 KEGLESNIT... 5 Cirkel... 6 Ellipse... 8 Prbel... 15 Hyperbel... 19 Keglesnitsligninger
9 Geodætiske kurver og Gauss-krumning
 9 Geodætiske kurver og Guss-krumning 9. Geodætiske kurver En ret linie i plnen fr punktet p til punktet q hr den egenskb t enhver nden kurve fr p til q hr kurvelængde som er mindst p q. Et stykke f en
9 Geodætiske kurver og Guss-krumning 9. Geodætiske kurver En ret linie i plnen fr punktet p til punktet q hr den egenskb t enhver nden kurve fr p til q hr kurvelængde som er mindst p q. Et stykke f en
Formelsamling Matematik C Indhold
 Formelsmling Mtemtik C Indhold Eksempler på besvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 0 Funktioner og modeller... 3 Lineær funktion... 3 Procentregning...
Formelsmling Mtemtik C Indhold Eksempler på besvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 0 Funktioner og modeller... 3 Lineær funktion... 3 Procentregning...
Analyse 30. januar 2015
 30. jnur 2015 Større dnsk indkomstulighed skyldes i høj grd stigende kpitlindkomster Af Kristin Thor Jkosen Udgivelsen f Thoms Pikettys Kpitlen i det 21. århundrede hr fstedkommet en del diskussion f de
30. jnur 2015 Større dnsk indkomstulighed skyldes i høj grd stigende kpitlindkomster Af Kristin Thor Jkosen Udgivelsen f Thoms Pikettys Kpitlen i det 21. århundrede hr fstedkommet en del diskussion f de
Analysens Fundamentalsætning
 Anlysens Fundmentlsætning Frnk Nsser 11. juli 2011 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Anlysens Fundmentlsætning Frnk Nsser 11. juli 2011 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Indhold 1 Introduktion
Formelsamling Matematik C Indhold
 Formelsmling Mtemtik C Indhold Eksempler på esvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 9 Funktioner og modeller... Lineær funktion... Procentregning...
Formelsmling Mtemtik C Indhold Eksempler på esvrelser, lin, eksp, pot, geo... Tl, regneopertioner og ligninger... 6 Ligninger... 7 Geometri... 9 Funktioner og modeller... Lineær funktion... Procentregning...
Pointen med Integration
 Pointen med Integrtion Frnk Vill 3. oktober 2012 2008-2012. IT Teching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere
Pointen med Integrtion Frnk Vill 3. oktober 2012 2008-2012. IT Teching Tools. ISBN-13: 978-87-92775-00-9. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere
Implicit differentiation Med eksempler
 Implicit fferentition Implicit fferentition Indhold. Implicit fferentition.... Tngent til ellipse og hperel... 3. Prisme i hovedstillingen...3 3. Teoretisk rgument for hovedstillingen...4 Ole Witt-Hnsen
Implicit fferentition Implicit fferentition Indhold. Implicit fferentition.... Tngent til ellipse og hperel... 3. Prisme i hovedstillingen...3 3. Teoretisk rgument for hovedstillingen...4 Ole Witt-Hnsen
Projekt 8.5 Linearisering og anvendelsen af logaritmiske koordinatsystemer
 Projekt 8.5 Linerisering og nvendelsen f logritmiske koordintsystemer (Dette projekt forudsætter, t mn hr rbejdet med logritmefunktionerne, f i kpitel 3 eller i projekt 8.4, så mn er fortrolig med logritmereglerne)
Projekt 8.5 Linerisering og nvendelsen f logritmiske koordintsystemer (Dette projekt forudsætter, t mn hr rbejdet med logritmefunktionerne, f i kpitel 3 eller i projekt 8.4, så mn er fortrolig med logritmereglerne)
Integralregning. Version juni Mike Vandal Auerbach
 Integrlregning Version.0 27. juni 209 y f x Mike Vndl Auerch www.mthemticus.dk Integrlregning Version.0, 209 Disse noter er skrevet til mtemtikundervisningen på stx A- og B-niveu efter gymnsiereformen
Integrlregning Version.0 27. juni 209 y f x Mike Vndl Auerch www.mthemticus.dk Integrlregning Version.0, 209 Disse noter er skrevet til mtemtikundervisningen på stx A- og B-niveu efter gymnsiereformen
Pointen med Integration
 Pointen med Integrtion Frnk Nsser 20. pril 2011 c 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
Pointen med Integrtion Frnk Nsser 20. pril 2011 c 2008-2011. Dette dokument må kun nvendes til undervisning i klsser som bonnerer på MtBog.dk. Se yderligere betingelser for brug her. Bemærk: Dette er en
MM501 forelæsningsslides
 MM50 forelæsningsslides uge 39, 200 Produceret f Hns J. Munkholm berbejdet f Jessic Crter Integrtion ved substitution Afsnit5.6 Ubestemte integrler s. 37-39 Reglen om differentition f en smmenst funktion
MM50 forelæsningsslides uge 39, 200 Produceret f Hns J. Munkholm berbejdet f Jessic Crter Integrtion ved substitution Afsnit5.6 Ubestemte integrler s. 37-39 Reglen om differentition f en smmenst funktion
Lektion 6 Bogstavregning
 Lektion Bogstvregning Formler... Reduktion... Ligninger... Lektion Side 1 Formler En formel er en slgs regne-opskrift, hvor mn med bogstver viser, hvorledes noget skl regnes ud. F.eks. formler til beregning
Lektion Bogstvregning Formler... Reduktion... Ligninger... Lektion Side 1 Formler En formel er en slgs regne-opskrift, hvor mn med bogstver viser, hvorledes noget skl regnes ud. F.eks. formler til beregning
Diverse. Ib Michelsen
 Diverse Ib Michelsen Ikst 2008 Forsidebilledet http://www.smtid.dk/visen/billede.php?billedenr69 Version: 0.02 (2-1-2009) Diverse (Denne side er A-2 f 32 sider) Indholdsfortegnelse Regning med procent
Diverse Ib Michelsen Ikst 2008 Forsidebilledet http://www.smtid.dk/visen/billede.php?billedenr69 Version: 0.02 (2-1-2009) Diverse (Denne side er A-2 f 32 sider) Indholdsfortegnelse Regning med procent
Projekt 8.4 Logaritmefunktionerne
 Hvd er mtemtik? Projekter: Kpitel 8. Projekt 8.4 Logritmefunktionerne Projekt 8.4 Logritmefunktionerne Indhold. log( ) og 0 som omvendte funktioner... 2 2. Den nturlige logritmefunktion, ln( ) og den nturlige
Hvd er mtemtik? Projekter: Kpitel 8. Projekt 8.4 Logritmefunktionerne Projekt 8.4 Logritmefunktionerne Indhold. log( ) og 0 som omvendte funktioner... 2 2. Den nturlige logritmefunktion, ln( ) og den nturlige
INTEGRALREGNING. Opgaver til noterne kan findes her. PDF. Facit til opgaverne kan hentes her. PDF. Version: 5.0
 INTEGRALREGNING Version: 5.0 Noterne gennemgår egreerne: integrl og stmfunktion, og nskuer dette som et redsk til estemmelse f l.. reler under funktioner. Opgver til noterne kn findes her. PDF Fcit til
INTEGRALREGNING Version: 5.0 Noterne gennemgår egreerne: integrl og stmfunktion, og nskuer dette som et redsk til estemmelse f l.. reler under funktioner. Opgver til noterne kn findes her. PDF Fcit til
FUNKTIONER del 2 Eksponentielle udviklinger Trigonometriske funktioner Potensfunktioner Polynomier Modeller Regression
 FUNKTIONER del Eksponentielle udviklinger Trigonometriske funktioner Potensfunktioner Polynomier Modeller Regression -klsserne Gmmel Hellerup Gymnsium Indhold EKSPONENTIELLE UDVIKLINGER... 3 Forskrift
FUNKTIONER del Eksponentielle udviklinger Trigonometriske funktioner Potensfunktioner Polynomier Modeller Regression -klsserne Gmmel Hellerup Gymnsium Indhold EKSPONENTIELLE UDVIKLINGER... 3 Forskrift
Differentialregning. integralregning
 Differentilregning og integrlregning Ib Micelsen Ikst 013 Indoldsfortegnelse Tegneøvelser...3 Introduktion... Definition f differentilkvotient og tngent...6 Tngentældninger...7 Den fledte funktion...7
Differentilregning og integrlregning Ib Micelsen Ikst 013 Indoldsfortegnelse Tegneøvelser...3 Introduktion... Definition f differentilkvotient og tngent...6 Tngentældninger...7 Den fledte funktion...7
Integralregning. 2. del. 2006 Karsten Juul
 Integrlregning del ( ( 6 Krsten Juul Indhold 6 Uestemt integrl8 6 Sætning om eksistens stmunktioner 8 6 Oplæg til "regneregler or integrl"8 6 Regneregler or uestemt integrl 9 68 Foreredelse til "integrtion
Integrlregning del ( ( 6 Krsten Juul Indhold 6 Uestemt integrl8 6 Sætning om eksistens stmunktioner 8 6 Oplæg til "regneregler or integrl"8 6 Regneregler or uestemt integrl 9 68 Foreredelse til "integrtion
Sfærisk Geometri Ole Witt-Hansen nov. 2016
 Sfærisk Geometri Ole Witt-Hnsen nov. 6 Indhold. Geometri på en kugle.... Sfæriske toknter og treknter...3. Polrtreknter...4 3. Den retvinklede sfæriske treknt...5 4. Beregning f sider og vinkler i den
Sfærisk Geometri Ole Witt-Hnsen nov. 6 Indhold. Geometri på en kugle.... Sfæriske toknter og treknter...3. Polrtreknter...4 3. Den retvinklede sfæriske treknt...5 4. Beregning f sider og vinkler i den
... ... ... ... ... ... ... b > 0 og x > 0, vil vi kalde en potensfunktion. 492 10. Potensfunktioner
 POTENSFUNKTIONER 0 49 0. Potensfunktioner POTENSFUNKTIONER DEFINITION En funktion med forskriften f( )= b hvor b > 0 og > 0 vil vi klde en potensfunktion. I MAT C kpitel så vi t hvis skl være et vilkårligt
POTENSFUNKTIONER 0 49 0. Potensfunktioner POTENSFUNKTIONER DEFINITION En funktion med forskriften f( )= b hvor b > 0 og > 0 vil vi klde en potensfunktion. I MAT C kpitel så vi t hvis skl være et vilkårligt
Simple udtryk og ligninger
 Simple udtryk og ligninger for gymnsiet og hf 0 Krsten Juul Indhold Rækkefølge f + og... Smle led f smme type... Gnge ind i prentes. del... Rækkefølge f og smt f + og... Gnge ind i prentes. del... Hæve
Simple udtryk og ligninger for gymnsiet og hf 0 Krsten Juul Indhold Rækkefølge f + og... Smle led f smme type... Gnge ind i prentes. del... Rækkefølge f og smt f + og... Gnge ind i prentes. del... Hæve
gudmandsen.net y = b x a Illustration 1: potensfunktioner i 5 forskellige grupper
 gudmndsen.net Dette dokument er publiceret på http://www.gudmndsen.net/res/mt_vejl/. Ophvsret: Indholdet stilles til rådighed under Open Content License[http://opencontent.org/openpub/]. Kopiering, distribution
gudmndsen.net Dette dokument er publiceret på http://www.gudmndsen.net/res/mt_vejl/. Ophvsret: Indholdet stilles til rådighed under Open Content License[http://opencontent.org/openpub/]. Kopiering, distribution
Dannelsen af Galakser i det tidlige. Univers. Big Bang kosmologi Galakser Fysikken bag galaksedannelse. første galakser. Johan P. U.
 Dannelsen af Galakser i det tidlige Johan P. U. Fynbo, Adjunkt Univers Big Bang kosmologi Galakser Fysikken bag galaksedannelse Observationer af de første galakser Et dybt billede af himlen væk fra Mælkevejens
Dannelsen af Galakser i det tidlige Johan P. U. Fynbo, Adjunkt Univers Big Bang kosmologi Galakser Fysikken bag galaksedannelse Observationer af de første galakser Et dybt billede af himlen væk fra Mælkevejens
Projekt 6.5 Vektorers beskrivelseskraft
 Hvd er mtemtik? ISBN 978877066879 Projekt 65 Vektorers eskrivelseskrft Indhold Vektorer i gymnsiet Linjestykker og prllelogrmmer Bevis inden for den klssiske geometri Bevis med nvendelse f vektorer 3 Digonlerne
Hvd er mtemtik? ISBN 978877066879 Projekt 65 Vektorers eskrivelseskrft Indhold Vektorer i gymnsiet Linjestykker og prllelogrmmer Bevis inden for den klssiske geometri Bevis med nvendelse f vektorer 3 Digonlerne
TAL OG REGNEREGLER. Vi ser nu på opbygningen af et legeme og noterer os samtidig, at de reelle tal velkendte regneoperationer + og er et legeme.
 TAL OG REGNEREGLER Inden for lgeren hr mn indført egreet legeme. Et legeme er en slgs konstruktion, hvor mn fstsætter to regneregler og nogle sætninger (ksiomer), der gælder for disse. Pointen med en sådn
TAL OG REGNEREGLER Inden for lgeren hr mn indført egreet legeme. Et legeme er en slgs konstruktion, hvor mn fstsætter to regneregler og nogle sætninger (ksiomer), der gælder for disse. Pointen med en sådn
Eksponentielle Sammenhænge
 Kort om Eksponentielle Smmenhænge 011 Krsten Juul Dette hæfte indeholder pensum i eksponentielle smmenhænge for gymnsiet og hf. Indhold 1. Procenter på en ny måde... 1. Hvd er en eksponentiel smmenhæng?....
Kort om Eksponentielle Smmenhænge 011 Krsten Juul Dette hæfte indeholder pensum i eksponentielle smmenhænge for gymnsiet og hf. Indhold 1. Procenter på en ny måde... 1. Hvd er en eksponentiel smmenhæng?....
Krumningsradius & superellipsen
 Krumningsrdius & suerellisen Side /5 Steen Toft Jørgensen Krumningsrdius & suerellisen Formålet med dette mini-rojekt er t erhverve mtemtisk viden om krumningsrdius f en kurve og nvende denne viden å det
Krumningsrdius & suerellisen Side /5 Steen Toft Jørgensen Krumningsrdius & suerellisen Formålet med dette mini-rojekt er t erhverve mtemtisk viden om krumningsrdius f en kurve og nvende denne viden å det
TAL OG BOGSTAVREGNING
 TAL OG BOGSTAVREGNING De elementære regnerter I mtemtik kn vi regne med tl, men vi kn også regne med bogstver, som gør det hele en smugle mere bstrkt. Først skl vi se lidt på de fire elementære regnerter,
TAL OG BOGSTAVREGNING De elementære regnerter I mtemtik kn vi regne med tl, men vi kn også regne med bogstver, som gør det hele en smugle mere bstrkt. Først skl vi se lidt på de fire elementære regnerter,
Undervisningsbeskrivelse
 Undervisningseskrivelse Stmoplysninger til rug ved prøver til gymnsile uddnnelser Termin Juni 2016 Institution Uddnnelse Fg og niveu Lærere Hold Fvrskov Gymnsium Stx Mtemtik A Peter Lundøer (Lu) 3k Mtemtik
Undervisningseskrivelse Stmoplysninger til rug ved prøver til gymnsile uddnnelser Termin Juni 2016 Institution Uddnnelse Fg og niveu Lærere Hold Fvrskov Gymnsium Stx Mtemtik A Peter Lundøer (Lu) 3k Mtemtik
Trigonometri FORHÅNDSVIDEN
 Trigonometri I dette kpitel skl du rejde med trigonometri. Ordet trigonometri stmmer fr græsk og etyder trekntsmåling. Den mtemtik, der ligger g trigonometrien, hr du llerede rejdet med. Det drejer sig
Trigonometri I dette kpitel skl du rejde med trigonometri. Ordet trigonometri stmmer fr græsk og etyder trekntsmåling. Den mtemtik, der ligger g trigonometrien, hr du llerede rejdet med. Det drejer sig
Valg mellem forbrug og fritid og modelleringen af timebeslutningen
 Dnmrks Sttistik MODELGRUPPEN Arbejdsppir[Udkst] Morten Werner og Rsmus H. Mdsen 25. november 2003 Vlg mellem forbrug og fritid og modelleringen f timebeslutningen Resumé: I ppiret udvides modellen for
Dnmrks Sttistik MODELGRUPPEN Arbejdsppir[Udkst] Morten Werner og Rsmus H. Mdsen 25. november 2003 Vlg mellem forbrug og fritid og modelleringen f timebeslutningen Resumé: I ppiret udvides modellen for
Matematik. Kompendium i faget. Tømrerafdelingen. 1. Hovedforløb. a 2 = b 2 + c 2 2 b c cos A. cos A = b 2 + c 2 - a 2 2 b c
 Kompendium i fget Mtemtik Tømrerfdelingen 1. Hovedforlø. Trigonometri nvendes til eregning f snd længde og snd vinkel i profiler. Sinus Cosinus Tngens 2 2 + 2 2 os A os A 2 + 2-2 2 Svendorg Erhvervsskole
Kompendium i fget Mtemtik Tømrerfdelingen 1. Hovedforlø. Trigonometri nvendes til eregning f snd længde og snd vinkel i profiler. Sinus Cosinus Tngens 2 2 + 2 2 os A os A 2 + 2-2 2 Svendorg Erhvervsskole
MATEMATISK FORMELSAMLING
 MATEMATISK FORMELSAMLING GUX Grønlnd Mtemtisk formelsmling til B-niveu, GUX Grønlnd Deprtementet for uddnnelse 05 Redktion: Rsmus Andersen, Jens Thostrup MtemtiskformelsmlingtilB-niveu GUX Grønlnd FORORD
MATEMATISK FORMELSAMLING GUX Grønlnd Mtemtisk formelsmling til B-niveu, GUX Grønlnd Deprtementet for uddnnelse 05 Redktion: Rsmus Andersen, Jens Thostrup MtemtiskformelsmlingtilB-niveu GUX Grønlnd FORORD
Matematikkens mysterier - på et højt niveau. 3. Differentialligninger
 Mtemtikkens msterier - på et højt niveu f Kenneth Hnsen 3. Differentilligninger N N N 3 A A k k Indholdsfortegnelse 3. Introduktion 3. Dnmiske sstemer 3 3.3 Seprtion f de vrible 8 3.4 Vækstmodeller 8 3.5
Mtemtikkens msterier - på et højt niveu f Kenneth Hnsen 3. Differentilligninger N N N 3 A A k k Indholdsfortegnelse 3. Introduktion 3. Dnmiske sstemer 3 3.3 Seprtion f de vrible 8 3.4 Vækstmodeller 8 3.5
1 Plan og rumintegraler
 1 PLAN OG RUMINTEGRALER 1 1 Pln og rumintegrler Ligesom for funktioner f en vribel kn mn for kontinuerte funktioner f flere vrible definere deres integrle. Vi vil her kun beskæftige os med funktioner f
1 PLAN OG RUMINTEGRALER 1 1 Pln og rumintegrler Ligesom for funktioner f en vribel kn mn for kontinuerte funktioner f flere vrible definere deres integrle. Vi vil her kun beskæftige os med funktioner f
( ) Projekt 7.17 Simpsons formel A A A. Hvad er matematik? 3 ISBN
 Projekt 7.7 Simpsons formel Simpson vr søn f en selvlært væver, og skulle egentlig selv hve været en væver, men en solformørkelse vkte hns interesse for mtemtik og nturvidensk og mod lle odds lykkedes
Projekt 7.7 Simpsons formel Simpson vr søn f en selvlært væver, og skulle egentlig selv hve været en væver, men en solformørkelse vkte hns interesse for mtemtik og nturvidensk og mod lle odds lykkedes
Oversigt. geometri exempler. areal: 4 3 = 12 m 2 omkreds: 4+3+4+3 = 14 m. areal: 5 5 = 25 cm 2 omkreds: 5+5+5+5 = 20 cm. areal: 8 5 = 40 dm 2
 geometri exempler 4 m 3 m rel: 4 3 = 12 m 2 omkreds: 4+3+4+3 = 14 m 5 m 5 m rel: 5 5 = 25 m 2 omkreds: 5+5+5+5 = 20 m 8 dm 5 dm rel: 8 5 = 40 dm 2 8 dm 5 mm 4 mm 1 2 rel: 4 (5+9) = 28 mm 2 9 mm 7 km rel:
geometri exempler 4 m 3 m rel: 4 3 = 12 m 2 omkreds: 4+3+4+3 = 14 m 5 m 5 m rel: 5 5 = 25 m 2 omkreds: 5+5+5+5 = 20 m 8 dm 5 dm rel: 8 5 = 40 dm 2 8 dm 5 mm 4 mm 1 2 rel: 4 (5+9) = 28 mm 2 9 mm 7 km rel:
Projekt 10.3 Terningens fordobling
 Hvd er mtemtik? Projekter: Kpitel 0 Projekt 0.3 Terningens fordoling Elementerne indeholder, hvd mn kn deducere sig til og konstruere sig til ud fr de få givne ksiomer. Mn kn derfor i en vis forstnd sige,
Hvd er mtemtik? Projekter: Kpitel 0 Projekt 0.3 Terningens fordoling Elementerne indeholder, hvd mn kn deducere sig til og konstruere sig til ud fr de få givne ksiomer. Mn kn derfor i en vis forstnd sige,
K9-K10 projekter i strukturel mekanik
 April 2006 K8 Studerende K9-K10 projekter i strukturel meknik K8-studerende med interesse i t lve K9 eller K10 projekter inden for områderne Strukturel dynmik og erodynmik f store konstruktioner Aeroelsticitet,
April 2006 K8 Studerende K9-K10 projekter i strukturel meknik K8-studerende med interesse i t lve K9 eller K10 projekter inden for områderne Strukturel dynmik og erodynmik f store konstruktioner Aeroelsticitet,
Geometrinoter 2. Brahmaguptas formel Arealet af en indskrivelig firkant ABCD kan tilsvarende beregnes ud fra firkantens sidelængder:
 Geometrinoter 2, jnur 2009, Kirsten Rosenkilde 1 Geometrinoter 2 Disse noter omhndler sætninger om treknter, trekntens ydre røringscirkler, to cirklers rdiklkse smt Simson- og Eulerlinjen i en treknt.
Geometrinoter 2, jnur 2009, Kirsten Rosenkilde 1 Geometrinoter 2 Disse noter omhndler sætninger om treknter, trekntens ydre røringscirkler, to cirklers rdiklkse smt Simson- og Eulerlinjen i en treknt.
114 Matematiske Horisonter
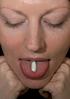 114 Mtemtiske Horisonter Mtemtik i medicinudvikling Af Ph.d-studerende Ann Helg Jónsdóttir, Ph.d-studerende Søren Klim, Ph.d-studerende Stig Mortensen og Professor Henrik Mdsen, DTU Informtik Hovedpinen
114 Mtemtiske Horisonter Mtemtik i medicinudvikling Af Ph.d-studerende Ann Helg Jónsdóttir, Ph.d-studerende Søren Klim, Ph.d-studerende Stig Mortensen og Professor Henrik Mdsen, DTU Informtik Hovedpinen
Lektion 6 Bogstavregning
 Mtemtik på Åbent VUC Lektion 6 Bogstvregning Formler... Udtryk... Ligninger... Ligninger som løsningsmetode i regneopgver... Simultion... Opsmlingsopgver... Lvet f Niels Jørgen Andresen, VUC Århus. Redigeret
Mtemtik på Åbent VUC Lektion 6 Bogstvregning Formler... Udtryk... Ligninger... Ligninger som løsningsmetode i regneopgver... Simultion... Opsmlingsopgver... Lvet f Niels Jørgen Andresen, VUC Århus. Redigeret
Dødelighed og kræftforekomst i Avanersuaq. Et registerstudie
 Dødelighed og kræftforekomst i Avnersuq. Et registerstudie Peter Bjerregrd, Anni Brit Sternhgen Nielsen og Knud Juel Indledning Det hr været fremført f loklbefolkningen i Avnersuq og f Lndsstyret, t der
Dødelighed og kræftforekomst i Avnersuq. Et registerstudie Peter Bjerregrd, Anni Brit Sternhgen Nielsen og Knud Juel Indledning Det hr været fremført f loklbefolkningen i Avnersuq og f Lndsstyret, t der
præget tro på, at udvikling også er fremskridt. Menneskeånden vil helt i tråd med oplysningstidens ideer medføre mange sejre og et konstant
 eller hvordn dens eventuelle ineffektivitet kunne modvirkes. Det er l.. dette tnkerejde, der hr ført til nutidens lngt mere effektive vrmemskiner, f.eks. ilmotoren og jetmotoren. rnot rejdede som nævnt
eller hvordn dens eventuelle ineffektivitet kunne modvirkes. Det er l.. dette tnkerejde, der hr ført til nutidens lngt mere effektive vrmemskiner, f.eks. ilmotoren og jetmotoren. rnot rejdede som nævnt
Michel Mandix (2010) INDHOLDSFORTEGNELSE:... 2 EN TREKANTS VINKELSUM... 3 PYTHAGORAS LÆRESÆTNING... 4 SINUSRELATIONERNE... 4 COSINUSRELATIONERNE...
 MATEMATIK NOTAT MATEMATISKE EVISER AF: CAND. POLYT. MICHEL MANDIX SIDSTE REVISION: FERUAR 04 Michel Mndi (00) Side f 35 Indholdsfortegnelse: INDHOLDSFORTEGNELSE:... EN TREKANTS VINKELSUM... 3 PYTHAGORAS
MATEMATIK NOTAT MATEMATISKE EVISER AF: CAND. POLYT. MICHEL MANDIX SIDSTE REVISION: FERUAR 04 Michel Mndi (00) Side f 35 Indholdsfortegnelse: INDHOLDSFORTEGNELSE:... EN TREKANTS VINKELSUM... 3 PYTHAGORAS
Kompendium. Matematik HF C niveau. Frederiksberg HF Kursus. Lars Bronée 2014
 Kompendium Mtemtik HF C niveu π Frederiksberg HF Kursus Lrs Bronée 04 Mil: post@lrsbronee.dk Web: www.lrsbronee.dk Indholdsfortegnelse: Forord Det grundlæggende Ligningsløsning 8 Procentregning Rentesregning
Kompendium Mtemtik HF C niveu π Frederiksberg HF Kursus Lrs Bronée 04 Mil: post@lrsbronee.dk Web: www.lrsbronee.dk Indholdsfortegnelse: Forord Det grundlæggende Ligningsløsning 8 Procentregning Rentesregning
GEOMETRI. Generelt om vinkler. Notation for vinkler: u, A, BAC. Topvinkler er lige store, x = y
 GEOMETRI Generelt om inkler Nottion for inkler: u, A, BAC Topinkler er lige store, x y Komplementinkler er inkler, der tilsmmen er 90 u + 90 Supplementinkler er inkler, der tilsmmen er 180 (I stedet for
GEOMETRI Generelt om inkler Nottion for inkler: u, A, BAC Topinkler er lige store, x y Komplementinkler er inkler, der tilsmmen er 90 u + 90 Supplementinkler er inkler, der tilsmmen er 180 (I stedet for
Kap. 3: Logaritme-, eksponential- og potensfunktioner. Differential- og integralregning.
 - 94 - Kp. 3: Logritme-, eksponentil- og potensfunktioner. Differentil- og integrlregning. 3.. Differentition f logritmefunktioner. Sætning 3... ) Enhver logritmefunktion er differentibel ) Den nturlige
- 94 - Kp. 3: Logritme-, eksponentil- og potensfunktioner. Differentil- og integrlregning. 3.. Differentition f logritmefunktioner. Sætning 3... ) Enhver logritmefunktion er differentibel ) Den nturlige
Lukkede flader med konstant krumning
 Lukkede flder med konstnt krumning Hns Anton Slomonsen Arhus Universitet Mrch 13, 2015 En flde i rummet B A giver nledning til to mål for fstnden mellem to punkter A og B på flden: - længden f den rette
Lukkede flder med konstnt krumning Hns Anton Slomonsen Arhus Universitet Mrch 13, 2015 En flde i rummet B A giver nledning til to mål for fstnden mellem to punkter A og B på flden: - længden f den rette
1,0. sin(60º) 1,0 cos(60º) I stedet for cosinus til 60º og sinus til 60º skriver man cos(60º) og sin(60º).
 Mtemtik på VU Eksempler til niveu F, E og D Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus ved først t tegne vinklen i et koordint-system som vist til venstre. Derefter
Mtemtik på VU Eksempler til niveu F, E og D Til lle vinkler hører der to tl, som kldes osinus og sinus. Mn finder sinus og osinus ved først t tegne vinklen i et koordint-system som vist til venstre. Derefter
- 81 - , x I. kmx. Sætningen bevises ikke her. Interesserede læsere henvises til bogen: Differentialligninger og matematiske
 - 8 - Appendi : Logistisk vækst og integrlregning. I forbindelse med eksponentielle vækstfunktioner er der tle om en vækstform, hvor funktionens væksthstighed er proportionl med den ktuelle funktionsværdi,
- 8 - Appendi : Logistisk vækst og integrlregning. I forbindelse med eksponentielle vækstfunktioner er der tle om en vækstform, hvor funktionens væksthstighed er proportionl med den ktuelle funktionsværdi,
Sandsynlighedsregning 5. forelæsning Bo Friis Nielsen
 Dgens emner fsnit 3.5 og 4. oissonfordelingen Sndsynlighedsregning 5. forelæsning Bo Friis Nielsen Mtemtik og Computer Science Dnmrks Tekniske Universitet 800 Kgs. Lyngby Dnmrk Emil: bfni@dtu.dk Kontinuerte
Dgens emner fsnit 3.5 og 4. oissonfordelingen Sndsynlighedsregning 5. forelæsning Bo Friis Nielsen Mtemtik og Computer Science Dnmrks Tekniske Universitet 800 Kgs. Lyngby Dnmrk Emil: bfni@dtu.dk Kontinuerte
Matematik - introduktion. Martin Lauesen February 23, 2011
 Mtemtik - introduktion Mrtin Luesen Februry 23, 2011 1 Contents 1 Aritmetik og elementær lgebr 3 1.1 Symboler............................... 3 1.1.1 ligheder............................ 4 1.1.2 uligheder...........................
Mtemtik - introduktion Mrtin Luesen Februry 23, 2011 1 Contents 1 Aritmetik og elementær lgebr 3 1.1 Symboler............................... 3 1.1.1 ligheder............................ 4 1.1.2 uligheder...........................
Eksemplificering af DEA-metodens vægtberegning
 nlyseinstitut for Forskning Finlndsgde DK-800 rhus N Tel + 89 9 Fx: + 89 99 Mil: fsk@fsk.u.dk Web:.fsk.u.dk Eksemplificering f DE-metodens vægtberegning Peter S. Mortensen Kmm Lngberg Crin Sponholtz Nott
nlyseinstitut for Forskning Finlndsgde DK-800 rhus N Tel + 89 9 Fx: + 89 99 Mil: fsk@fsk.u.dk Web:.fsk.u.dk Eksemplificering f DE-metodens vægtberegning Peter S. Mortensen Kmm Lngberg Crin Sponholtz Nott
Formelsamling til Fourieranalyse 10. udgave
 Formelsmling til Fouriernlyse. udgve Kristin Jerslev og Steven Hyden 3. oktober 9 Her følger en formelsmling lvet til kurset Fouriernlyse på Arhus Universitet. Bemærk venligst, t smlingen indeholder sætninger
Formelsmling til Fouriernlyse. udgve Kristin Jerslev og Steven Hyden 3. oktober 9 Her følger en formelsmling lvet til kurset Fouriernlyse på Arhus Universitet. Bemærk venligst, t smlingen indeholder sætninger
Formelsamling i Matematik på C og B og A niveau Dette er en formelsamling der er under konstant udvikling Så hvis du har ønsker til denne så sig til
 Niels Junges formelsmling Formelsmling i Mtemtik på C og B og A niveu Dette er en formelsmling der er under konstnt udvikling Så hvis du hr ønsker til denne så sig til Indhold Tble of Contents Specielle
Niels Junges formelsmling Formelsmling i Mtemtik på C og B og A niveu Dette er en formelsmling der er under konstnt udvikling Så hvis du hr ønsker til denne så sig til Indhold Tble of Contents Specielle
Hvis man ønsker mere udfordring, kan man springe den første opgave af hvert emne over.
 Opsmling Hvis mn ønsker mere udfordring, kn mn springe den første opgve f hvert emne over Brøkregning, prentesregneregler, kvdrtsætningerne, potensregneregler og reduktion Udregn nedenstående tl i hånden:
Opsmling Hvis mn ønsker mere udfordring, kn mn springe den første opgve f hvert emne over Brøkregning, prentesregneregler, kvdrtsætningerne, potensregneregler og reduktion Udregn nedenstående tl i hånden:
Lektion 5 Det bestemte integral
 f(x) dx = F (b) F () Lektion 5 Det bestemte integrl Definition Integrlregningens Middelværdisætning Integrl- og Differentilregningens Hovedsætning Bereging f bestemte integrler Regneregler Arel mellem
f(x) dx = F (b) F () Lektion 5 Det bestemte integrl Definition Integrlregningens Middelværdisætning Integrl- og Differentilregningens Hovedsætning Bereging f bestemte integrler Regneregler Arel mellem
Setup til kalibrering af Clamp on-flowmålere
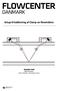 Setup til klirering f Clmp on-flowmålere Decemer 2018 Rpportforftter: Anders Niemnn, Teknologisk Institut Introduktion Ultrlyds-clmp-on flowmåling er en teknik, hvor mn ved hjælp f to trnsducere monteret
Setup til klirering f Clmp on-flowmålere Decemer 2018 Rpportforftter: Anders Niemnn, Teknologisk Institut Introduktion Ultrlyds-clmp-on flowmåling er en teknik, hvor mn ved hjælp f to trnsducere monteret
Et udvalg af funktionerne tegnet på grafregneren (eller her med Derive)
 GDS, opgve 85 En strt på opgven (undervisnings- og tvleprotokol): En milie unktioner hr orskrit 4 ( ) + R, Et udvlg unktionerne tegnet på grregneren (eller her med Derive) Værdier tllet, or hvilke hr henholdsvis
GDS, opgve 85 En strt på opgven (undervisnings- og tvleprotokol): En milie unktioner hr orskrit 4 ( ) + R, Et udvlg unktionerne tegnet på grregneren (eller her med Derive) Værdier tllet, or hvilke hr henholdsvis
Eksempel 9.1. Areal = (a 1 + b 1 )(a 2 + b 2 ) a 1 a 2 b 1 b 2 2a 2 b 1 = a 1 b 2 a 2 b 1 a 1 a 2 = b 1 b 2. Eksempel = ( 1) = 10
 Oversigt [LA] 9 Nem vej til rel Nøgleord og begreber Helt simple determinnter Determinnt defineret Effektive regneregler Genkend determinnt nul determinnt nul Produktreglen Inversreglen inversregel og
Oversigt [LA] 9 Nem vej til rel Nøgleord og begreber Helt simple determinnter Determinnt defineret Effektive regneregler Genkend determinnt nul determinnt nul Produktreglen Inversreglen inversregel og
